经验特征函数在偏正态分布中的应用

侯格格

(温州大学数理与电子信息工程学院，浙江温州 325035)

在实际问题处理中，会经常遇到大量非对称数据，若简单地假设这些数据的模型误差服从正态分布，通过数据分析，往往会发现这些数据具有多峰性、有偏性，并不完全服从正态分布．此时，可以使用偏正态分布处理非对称数据．偏正态分布是正态分布的一种推广，最早出现于文献[1]，由Azzalini[2]命名，它既具有正态分布的特殊性质又含有偏度的分布．设X是服从一元偏正态分布的随机变量，其密度函数为：fX(x;α)=2 ⋅φ(x) ⋅Φ(αx)，其中φ(x)， Φ(x)分别是标准正态分布的密度函数和标准正态分布的分布函数，α为任意实数，被称为形状参数，它控制密度函数的形状．当α=0时，分布函数偏度为零，X～N(0,1)，分布函数的偏度随着α的增加而增加，当α→∞时，分布函数收敛于半正态密度函数，在实际应用时，需要加入位置与尺度函数．考虑线性变换Y=ωX+ξ，Y的密度函数为：

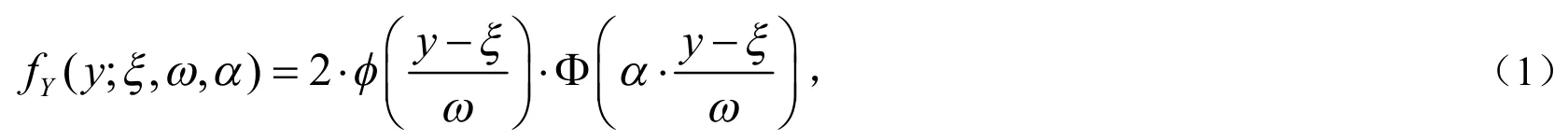
称Y服从偏正态分布，记为Y～SN(ξ,ω2,α)，ξ,ω,α分别是位置参数、尺度参数、形状参数，令θ=(ξ,ω,α)为待估参数．α=0时，Y～N(ξ,ω2)．

常见参数估计方法有矩估计、极大似然估计、M-估计等．对于单参数或者两个参数估计问题，容易求出稳定解．尽管一元偏正态分布族具有良好的性质，但由于其具有三个参数，求得稳定的估计值较为困难，这是由于：1）当α→0时，Fisher 信息阵是奇异的；2）α=0是α的轮廓似然函数的一个驻点，独立于观测样本．对于一元偏正态分布的三个参数的估计问题，使用极大似然估计求解时，遇到没有显式解的情况，尤其在小样本时，极大似然估计稳定性较差，矩估计与M-估计求出的估计值也较差．Azzalini 和Arellano[3]提出了含有惩罚项极大似然估计的方法，选择合适的惩罚函数对参数进行估计，此估计方法，当样本量大于200时，参数估计值稳定，由于形状参数α难以估计，当n＜200，即为小样本量时，含有惩罚项的极大似然估计算法是不稳定的．

经验特征函数算法最早由Feuerverger 和Mureika[4]与Heathcote[5]提出，Tran[6]将其应用于参数估计问题中．这个方法与文献[7-8]提出的矩母函数方法类似，使用特征函数代替矩母函数．使用特征函数进行估计具有一些优点．特征函数是一致有界，因此由其所求出的解具有数值稳定性．对于厚尾分布，当它的矩母函数不存在时，使用特征函数是恰当的．经验特征函数算法的稳定性受到{tm}的取值影响，对于此问题，文献[8-9]进行了分析．

本文第一部分首先对经验特征函数算法进行叙述，并对经验特征函数算法的有效性进行讨论．由于算法受到固定网格点{tm}的影响，进而对{tm}的选取进行讨论，对如何选取最优的网格点{tm}使得算法获得高渐进有效性进行说明．第二部分进行模拟，取不同的固定样本量的小样本，使用经验特征函数算法对一元偏正态分布三个参数进行估计，并与惩罚极大似然估计进行对比．

1 经验特征函数算法

本文我们将经验特征函数算法应用于一元偏正态分布中．假设一个样本容量为n随机样本y1,y2,…,yn来自于一元偏正态分布，其概率密度函数为（1）式．定义yi的特征函数为：

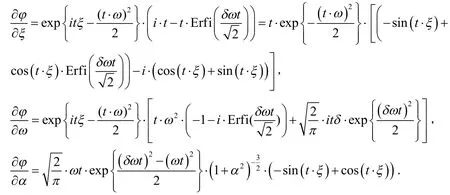
定义经验特征函数为：

其中i为虚数，{tm}是一系列固定的网格点，可以是连续的，也可以是离散的．现将φ(y;θ)和Cn(t)的实部与虚部分别分离出来，则它们在m个网格点t1,t2,…,tm的估计为：

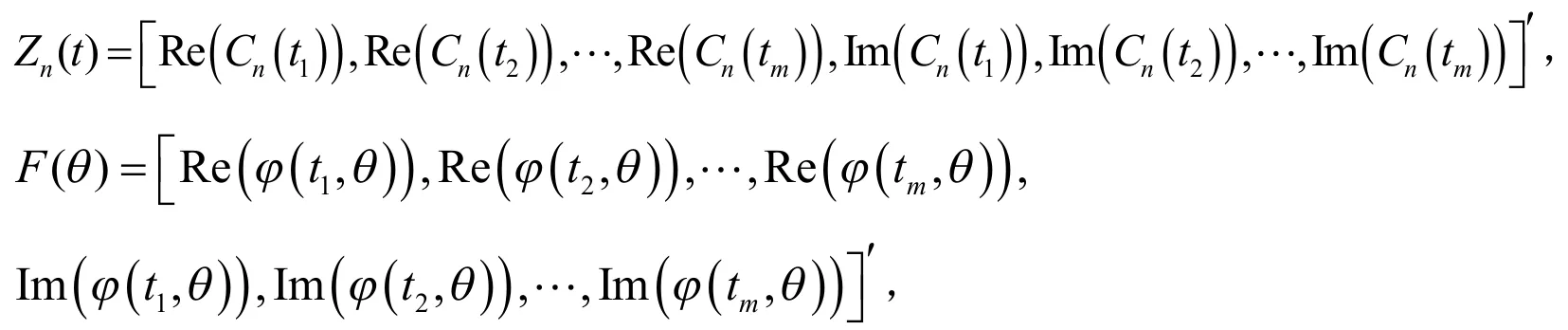
其中，

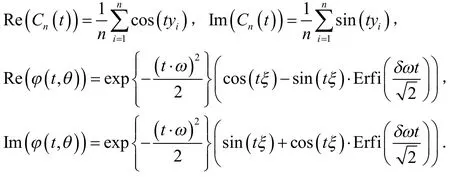
它的分割中的元素是与tp和tq相关，可以表示为（为了定义方便，假设θ在φ(t,θ)中）：

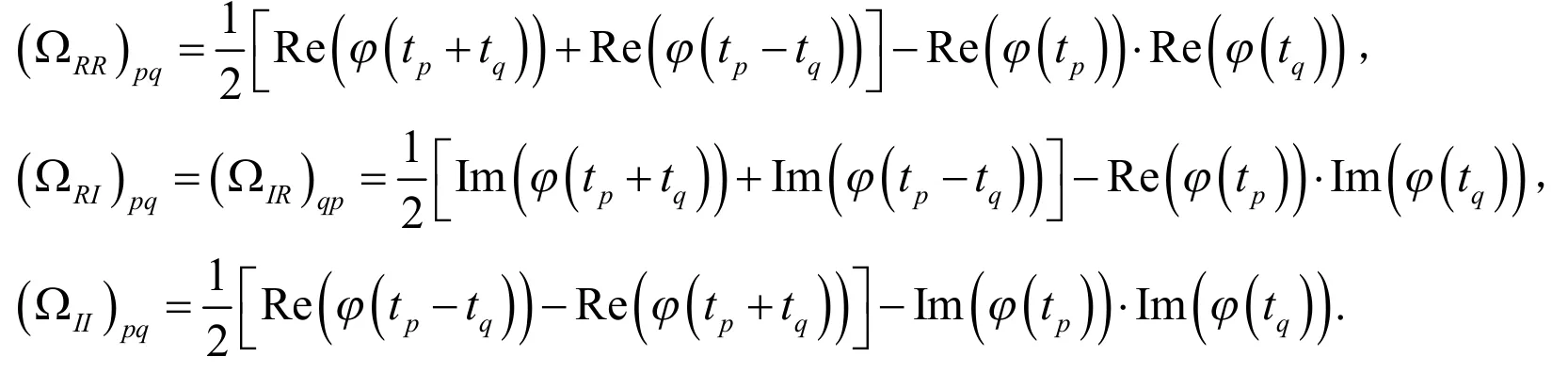
进一步，定义

式（5）可以被看作是一个协方差矩阵为非标量的非线性回归，其中Zn(t)可以被看作是响应变量，F(t,θ)可以被看作是解释变量．因此，对于给定的互不相同的网格点t1,t2,…,tm，其中m必须大于等于待估参数的个数，θ的有效估计，即经验特征函数算法的估计值，可以通过最小化

其中，

根据文献[8]对于的渐进有效性，有如下命题成立：

命题1 令t1,t2,…,tm为一系列取值不同的固定网格点，θ的经验特征函数算法的估计值是θ的强相合估计，并且服从渐进正态分布，其均值为θ，协方差为：

由命题1 可知经验特征函数算法的渐进有效性依赖于固定网格点{tm}的选择．文献[8]指出，对某些估计问题，经验特征函数算法可达到充分的渐进有效性（以达到Cramer-Rao 下界为标准）．

根据文献[8-9]的分析，{tm}必须是互不相同的．对于固定的m，为了方便起见，使用相等的区间间隔τ，则网格点为tj=j⋅τ,j=1,2,…,m，而τ可以是任何实数常数，通过最小化（8）的大小（例如行列式）求出最优的区间间隔τ．在最小化（8）式时会出现一个依赖待估参数的估计值，但待估参数未知的难题．解决此问题，一种方法是代入待估参数的初始值进行计算．值得注意的是当t的个数接近待估参数个数时，{tm}的选择对算法的有效性影响是非常大的．当m达到某个值之后，经验特征函数算法的渐进有效性并不随着t的个数增加而增加（或减小）．为验证此结论成立，假设有k个网格点t1,t2,…,tk，此时其渐进协方差矩阵为现假设前k个网格点值不变，增加一个或多个网格点，此时渐进协方差矩阵为其中由此看出，在最初的网格点的基础上增加若干个点，只是增加了矩阵A的列，矩阵Ω的行与列．为了说明矩阵是正定矩阵，首先我们先说明它是半正定矩阵．对于分块矩阵的逆正则化，则有：

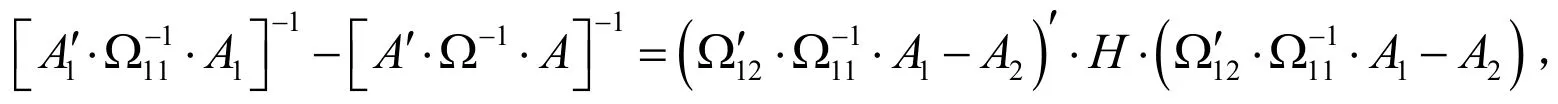
2 模 拟

样本量n分别取50、 1 00、200，ξ固定等于0，ω固定等于1，α分别取-3、-2、-1、1、2、3等六个不同的值，分别使用经验特征函数算法和含有惩罚项的极大似然估计算法对三个参数重复进行500次估计，以绝对偏差和均方误差（MSE）为标准，对比两种算法的稳定性．

当样本量n=50时，根据多次重复计算的结果，求出两种算法所对应的绝对偏差和MSE．为更佳直观的分析，现画出不同α值下三个参数所对应的绝对偏差和MSE 的图像，如图1 所示．

图1 当n=50，α取不同值时，两种不同方法所得估计值的绝对偏差和MSEFig 1 The Absolute Deviation and MSE of the Estimated Value through Two Different Methods Whenn=50andαChooses Different Values

由图1 可以看出两种算法关于α的估计值的绝对偏差都较大，但与含有惩罚项的极大似然估计算法相比，经验特征函数算法关于α的估计值的绝对偏差要小些，说明经验特征函数算法求得的估计值偏离真实值的程度更小，求得的α估计值的平均值更接近于真实值．两种算法对于位置、尺度两个参数估计的MSE 都很小，由于形状参数难以估计，经验特征函数算法对于α的估计容易受到初始值的影响，所以形状参数的MSE 出现很大的波动，因此两种算法都是不稳定的．从整体上看，当样本量很小时，经验特征函数算法略优于含有惩罚项的极大似然估计算法．

当样本量n=100时，根据多次重复计算的结果，求出两种算法所对应的绝对偏差和MSE.为更佳直观的分析，现画出不同α值下三个参数所对应的绝对偏差和MSE 的图像，如图2 所示．

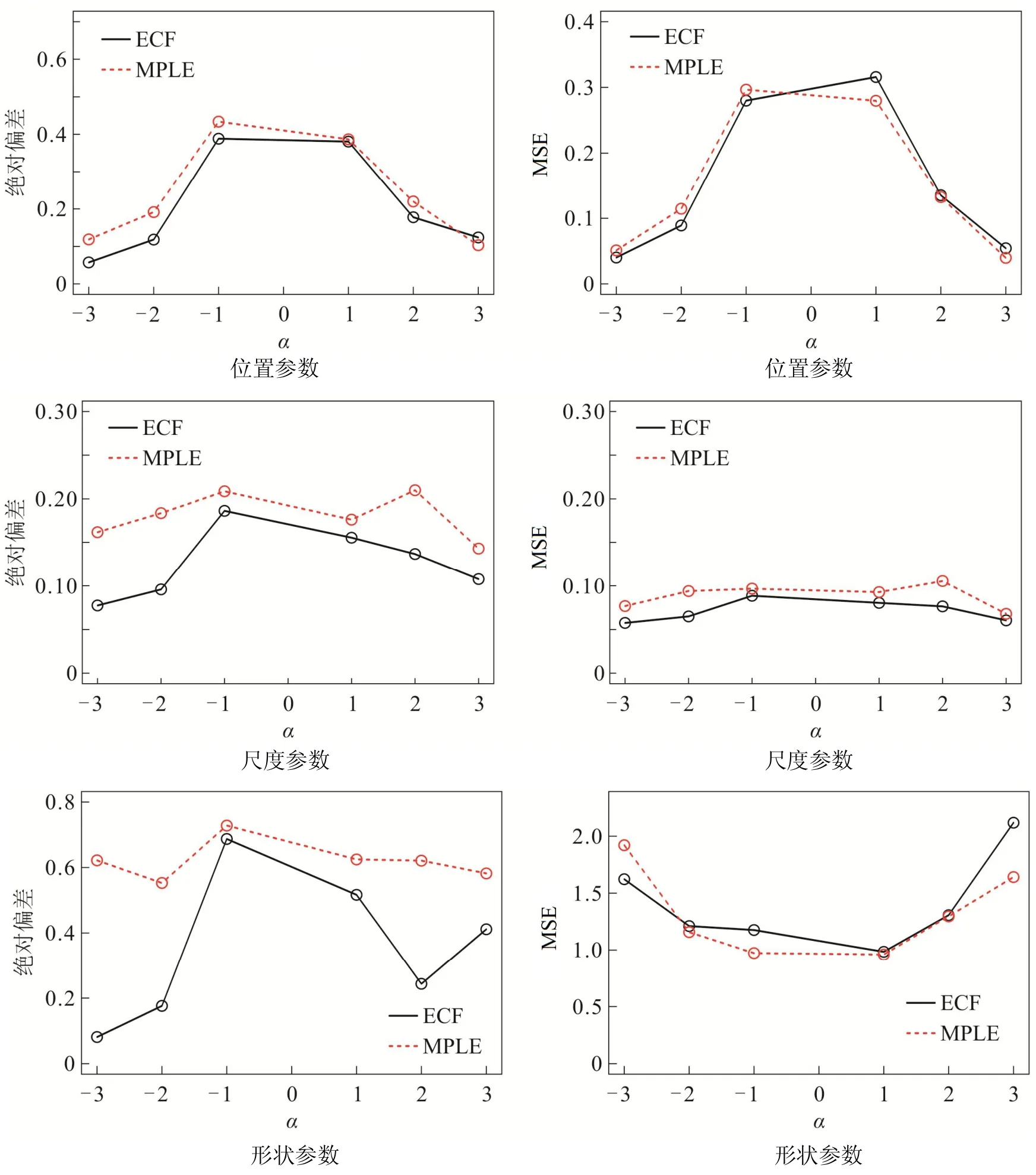
图2 当n=100，α取不同值时，两种不同方法所得估计值的绝对偏差和MSEFig 2 The Absolute Deviation and MSE of the Estimated Value through Two Different Methods Whenn=100andαChooses Different Values

由图2 可以看出，两种算法的绝对偏差都较小，但与含有惩罚项的极大似然估计算法相比，经验特征函数算法对于三个参数估计的绝对偏差要小些，说明经验特征函数算法求得的估计值偏离真实值的程度更小，求得的估计值的平均值在真实值附近．两种算法对于位置、尺度两个参数估计的MSE 都很小．由于样本量较小，两种算法对于α的估计出现一些波动，使得形状参数的MSE 大于1，两者间的差距不大，因此两种算法有效性一般．从整体上看，经验特征函数算法优于含有惩罚项的极大似然估计算法．

当样本量n=200时，根据多次重复计算的结果，求出两种算法所对应的绝对偏差和MSE．为更佳直观的分析，现画出不同α值下三个参数所对应的绝对偏差和MSE 的图像，如图3 所示．

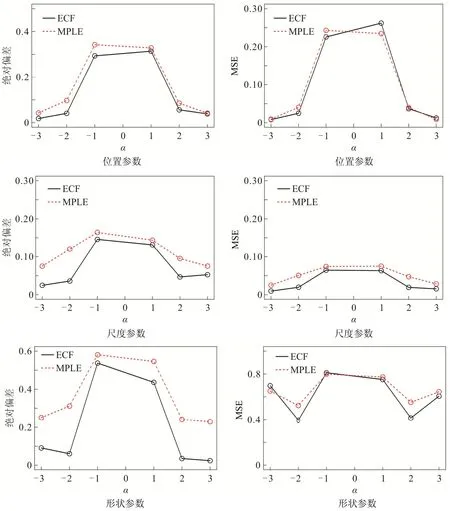
图3 当n=200，α取不同值时，两种不同方法所得估计值的绝对偏差和MSEFig 3 The Absolute Deviation and MSE of the Estimated Value through two Different Methods Whenn=200andαChooses Different Values

由图3 可以看出，两种算法的绝对偏差都较小，但与含有惩罚项的极大似然估计算法相比，经验特征函数算法对于三个参数估计的绝对偏差要小些，说明经验特征函数算法求得的估计值偏离真实值的程度更小，求得的估计值平均值在真实值附近．两种算法对于位置、尺度两个参数估计的MSE 都很小．由于形状参数难以估计，经验特征函数算法对于α的估计容易受到初始值的影响，所以形状参数的MSE 出现波动，但两者对于形状参数α的估计的MSE 都小于0.8，两者间的差距不大，因此两种算法都是稳定的．从整体上看，经验特征函数算法优于含有惩罚项的极大似然估计算法．因此，从整体上看，当n≤200时，经验特征函数算法对一元偏正态分布的参数估计的有效性好于含有惩罚项的极大似然估计算法．

3 结 论

本文介绍了经验特征函数算法，并对一元偏正态分布的位置、尺度、形状三个参数进行了估计，画出了由估计值拟合出来的概率密度函数图像，以绝对偏差、MSE 为标准，与现存的含有惩罚项的极大似然估计算法进行了对比，结果表明本文所给算法优于含有惩罚项的极大似然估计算法．