非线性需求下多寡头博弈模型的动力学分析

路正玉，于欢欢，王文静，赵 娜

(兰州交通大学数理学院，甘肃兰州 730070)

在社会和科技不断发展的同时，经济也在不断发展，像银行、保险等．伴随着经济的发展，出现了一些严重的社会问题，价格竞争[1]就是其中一个．价格竞争的出现源自于各大厂商都想着扩大自己的市场，想通过调整自己产品的价格和其它厂家竞争，于是就出现了寡头垄断现象[2]．市场往往被几个寡头垄断，这是市场普遍存在的一种形式．López 等[3]基于经济学家Bertrand 的研究提出了一个双重寡头垄断模型，这个模型是以通过价格竞争来赢得市场为目的的一种模型．消费者喜欢选择价格低的产品，寡头垄断者就通过降低他们产品价格来赢得更多的消费者．Agiza等[4-5]对多寡头博弈下市场稳定存在时商品的价格变化区间进行了研究，在该区间发现了混沌现象的存在．Ahmed 等[6-10]通过研究市场上各厂家为了吸引消费者所作的广告，得出了一个新的模型：广告竞争模型，并且还得出了Lyapunov 指数．通过这些研究结论能够分析出价格的复杂变化．杨树等[11-14]研究了房地产市场的一些垄断情况，发现真正的纳什均衡可以在有界有理不完全信息的动态重复博弈下进行．

企业之间的行为都是相关的，它们之间互相影响．企业主要通过价格竞争在市场上相互制约，商品合理的定价直接影响到价格竞争的成功与否．在当今的寡头市场上，产品的性质基本上是相同的，每一家企业的定价决策和目的都很容易被其它企业觉察到．可以看出，现在的寡头企业的市场份额之间存在着一种促进和抑制的关系，所以，寡头企业的生存与发展的着重点就在定价的策略上．寡头企业定制价格，不仅要有丰富经验的先驱决策者，还要有先进的科学的指导理论，博弈论就是能够为寡头企业定价策略提供正确指导的科学理论．本文将利用博弈论的相关理论建立模型，分析企业在同样的产品性质下的价格定制策略．

1 模型的建立

假设市场上有两个生产同类产品的企业，企业1 和企业2 生产的产品具有一定的替代关系，生产的产品分别记为A 和B．一个寡头企业不仅影响自己的决策，而且影响其它寡头企业的决策，甚至改变整个市场的运行状态．产品价格、销售量分别记为pi,qi(i=1, 2)，则寡头企业1 和企业2 的线性需求函数可设为：

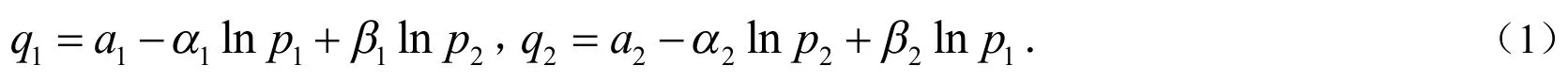
假设企业i(i=1, 2)成本函数形式为cipi，其中ci(i=1, 2)为企业技术水平对价格的敏感系数，则寡头企业i的利润函数表达式为：

整理可得：

因为市场上各企业占据了不同的市场信息，市场信息表现为不完全性，对于寡头垄断者的企业也是如此，在有限的信息下，他们在市场竞争中只能对价格的调整策略作出合理的决策．当两个企业的价格调整策略差不多时，认为他们是采用了有限的决策方式，主要就是通过市场上的利润反馈信息来对价格进行调整．下一期的价格调整信息是由这一期的市场利润和价格信息分析得出的．两个企业采用上述规则进行决策时，也就是说如果边际利润为正，市场上产品的需求量就会增加，相反，如果边际利润为负，市场上产品的需求就会减少．下列式子中v1和v2为价格调整速度，价格的调整策略可以表述为：

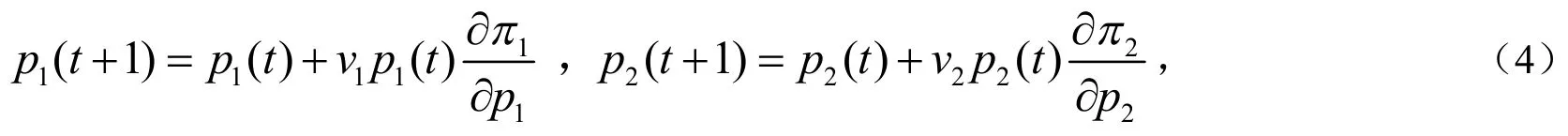
其中pi(t+ 1)和pi(t)分别表示第t+ 1期和第t期的价格．第t期，原寡头企业的边际利润函数为：

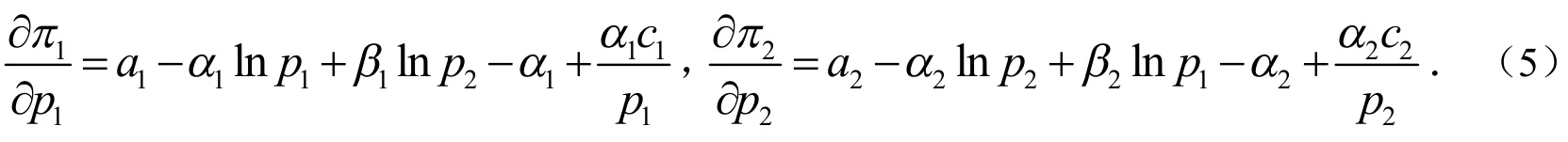
令∂π1∂p1=0，∂π2∂p2=0时就能得到企业1 和企业2 的反应方程：

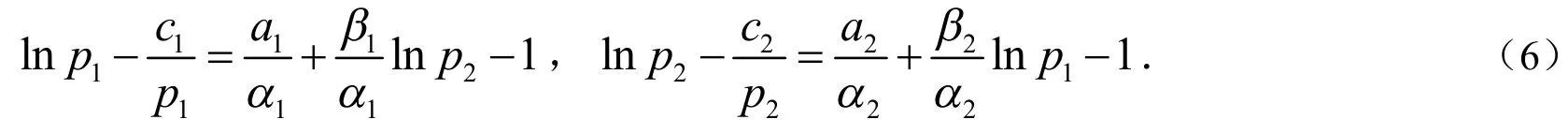
依据以上分析，得出如下基于不同预期的双寡头投资动态调整模型：

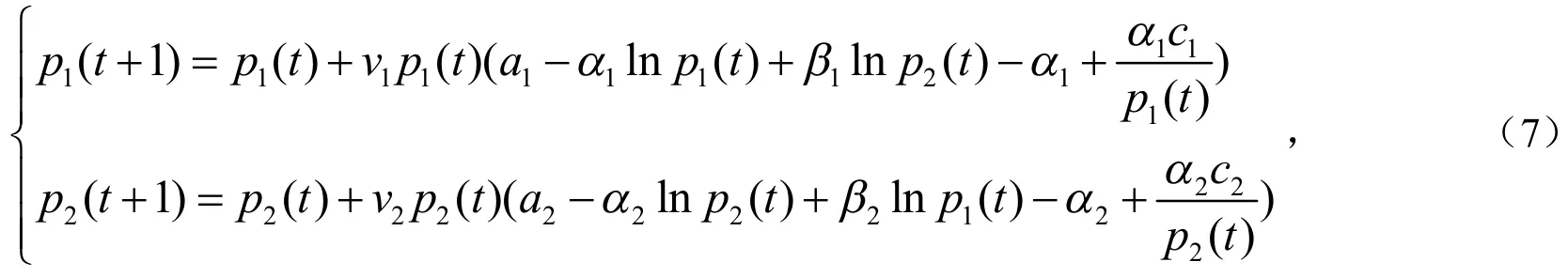
其中a1＞0和a2＞0分别表示产品的市场容量；α1＞0和α2＞0分别表示企业产品A 和B 对自身价格的敏感度；β1＞0和β2＞0分别表示企业产品A 和B 对对方产品价格的敏感度．在两个企业同时决策的情况下，假定两企业的边际成本分别为c1和c2，没有固定的成本．

2 模型分析

产品A 产品B 存在着一定的替代关系，但不是相同性质的产品，此时α1,α2,β1,β2均为有限的正实数．考虑反应方程：

由隐函数定理得，当D≠ 0时，反应方程组能够确定唯一的一个函数：p1(α1,α2,β1,β2)，p2(α1,α2,β1,β2)，所以，可以确定唯一的一组均衡价格p1，p2．

3 数值模拟

为了更好地了解系统的动力学特性，在这部分，主要通过模拟系统在不同参数范围下的复杂动力学行为来定性地分析系统的动力学特性．

3.1 调整速度v1和v2对系统稳定性的影响

图1 是系统寡头企业的商品售价p1和p2关于参数v1的分岔图和相应的最大Lyapunov 指数图．通过不断调整其它参数，尝试着用Matlab 绘制一些图形．取一组参数不变：a1=0.4，a2=0.3，α1=0.9，α2=0.9，β1=0.05，β2=0.7，c1=0.4，c2=0.5，v2=0.2，绘制系统（7）关于v1的单参数分岔图，如图1（a）所示．从图1（a）中看出，当参数0＜v1＜2.42时，系统是很稳定的，当系统处于稳定的区间时，市场表现为稳定有序，有利于社会的稳定发展，企业之间的相对竞争力度较小，各企业相对稳定存在；当参数2.42＜v1＜2.9时，系统就出现了混沌现象，当混沌现象发生时市场就会进入到一种混乱无序的杂乱状态，在这种情况下，无论是企业自己还是他们的竞争者都无法避免受混乱状态的影响，尤其对市场上的一些根基并不稳固的小厂家来说，生存是很困难的，市场的不稳定影响的就不只是市场了，整个社会都会受其影响，这个时候，寡头企业1 的管理者就应该控制价格的相关调整策略和他们产品的价格调整速度，尽量不要因为眼前的利益发动价格战，进而产生市场的混乱．

根据判断系统状态的最大的Lyapunov 指数，得到相对于图1（a）的最大Lyapunov 指数如图1（b）所示．最大Lyapunov 指数的不同表示系统的状态不相同，当最大Lyapunov 指数小于0时，系统处于稳定状态，最大Lyapunov 指数大于0时，系统处于混沌状态．

图2 是系统寡头企业商品售价p1和p2关于参数v2的分岔图和相应的最大Lyapunov 指数图．通过不断调整其它参数，固定一组参数不变：a1=0.2，a2=0.2，α1=0.8，α2=1,β1=0.3，β2=0.2，v1=0.1，c1=0.2，c2=0.3，绘制系统（7）关于v2的单参数分岔图，如图2（a）所示．从图2 中可以看出，当参数0＜v2＜1.36时，系统处于稳定周期，市场表现为稳定有序盈利，有利于社会的稳定发展，企业之间的相对竞争力度较小，各企业相对稳定运营；当参数1.36＜v2＜1.71时，就变成了混沌状态．图2（a）的最大Lyapunov 指数如图2（b）所示．

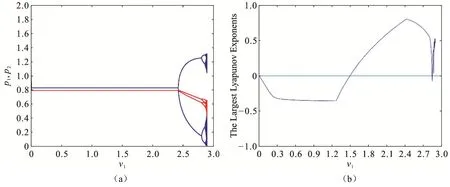
图1 系统（7）关于参数v1的分岔图和相应最大Lyapunov 指数图Fig 1 Bifurcation Diagram and Corresponding Maximum Lyapunov Exponent Diagram about Parametersv1of System (7)

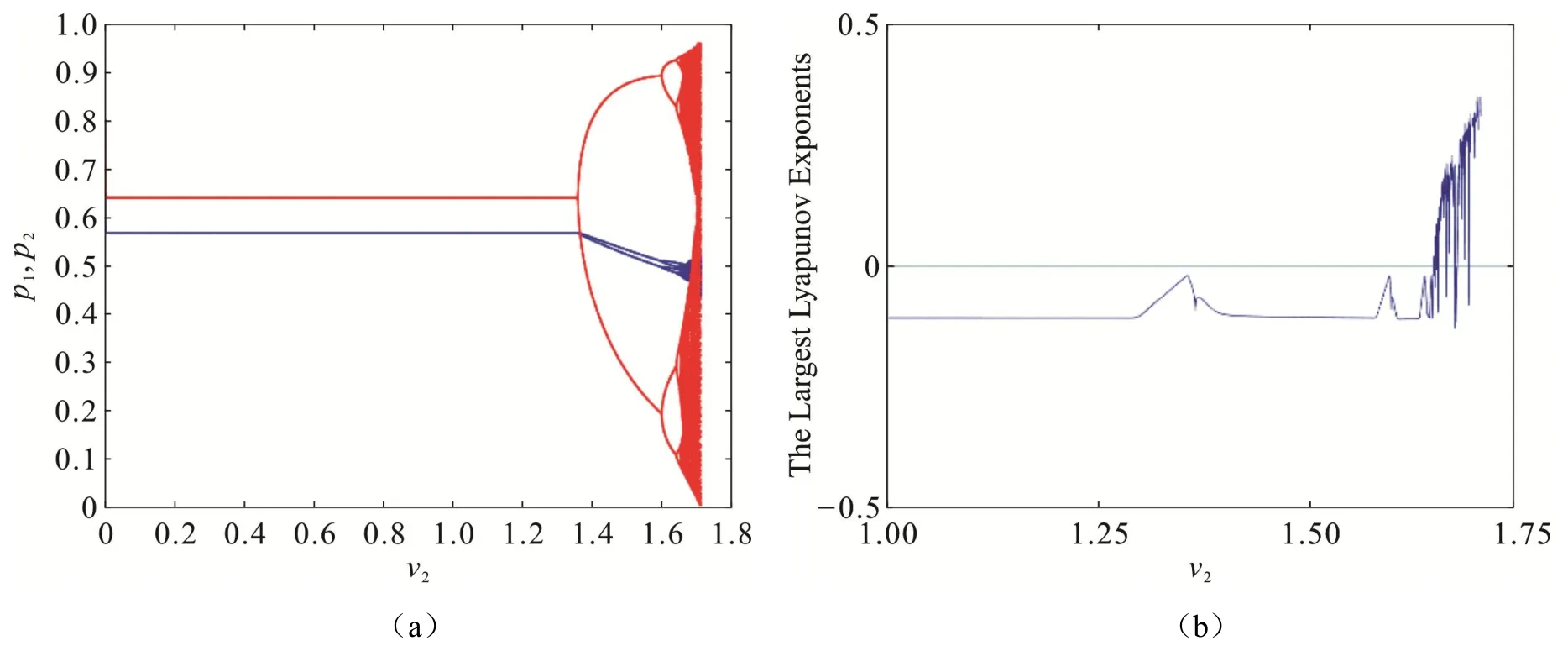
图2 系统（7）关于参数v2的分岔图和相应最大Lyapunov 指数图Fig 2 Bifurcation Diagram and Corresponding Maximum Lyapunov Exponent Diagram about Parametersv2of System (7)

3.2 敏感度1β和2β对系统稳定性的影响

下面讨论寡头厂商A（B）所生产的产品对寡头厂商B（A）生产的产品的替代率β1（β2）对系统稳定性的影响．

图3 是系统寡头厂商商品售价p1和p2关于参数β1的分岔图和相应的最大Lyapunov 指数图．通过不断调整其它参数，取一组参数不变：a1=1 ，a2=0.5，α1=2 ，α2=0.5，β2=0.5，v1=0.2，v2=0.2，c1=0.2，c2=0.1，绘制系统（7）关于β1的单参数分岔图，如图3（a）所示．可以看出，当参数0＜β1＜6.42时，系统是很稳定的，当系统处于稳定的区间，市场表现为稳定有序；当参数6.42＜β1＜6.79时，就变成了混沌状态，当混沌现象发生时市场就会进入到一种混乱无序的杂乱状态，在这种情况下，无论是厂商自己还是他们的竞争者都无法避免受混乱状态的影响，尤其对市场上的一些根基并不稳固的小厂家来说，生存是很困难的，市场的不稳定影响的就不只是市场了，整个社会都会受其影响，在这个时候，寡头厂商A 管理者应尽力控制产品替代率，尽量不要因为眼前利益就发动价格战，进而造成市场混乱．根据判断系统状态的最大Lyapunov 指数，得到相对于图3（a）的最大Lyapunov 指数，如图3（b）所示．最大Lyapunov指数的不同表示系统的状态不相同，当最大Lyapunov 指数小于0时，系统处于稳定状态，最大Lyapunov 指数大于0时，系统处于混沌状态．

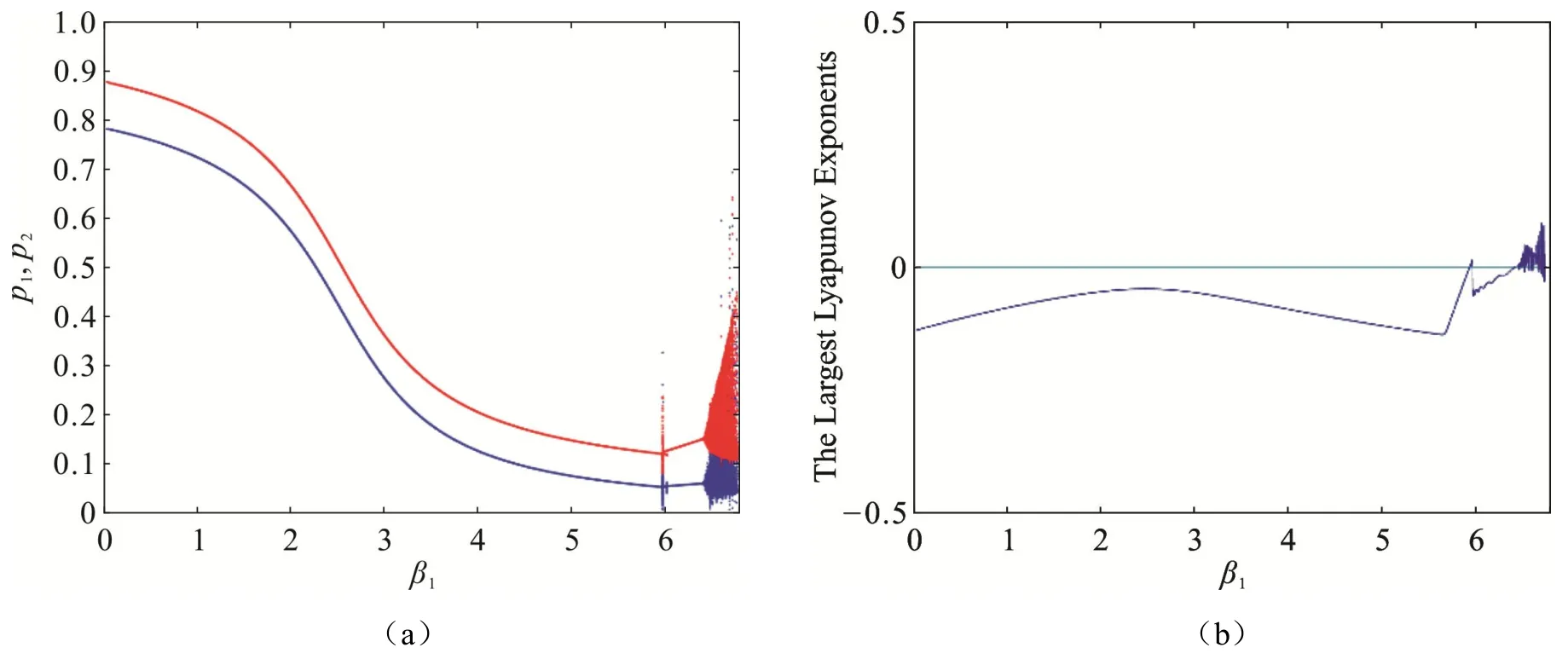
图3 系统（7）关于参数 1β的分岔图和相应最大Lyapunov 指数图Fig 3 Bifurcation Diagram and Corresponding Maximum Lyapunov Exponent Diagram about Parameters 1βof System (7)

图4 是系统寡头厂商商品售价p1和p2关于参数β2的分岔图和相应的最大Lyapunov 指数图．通过不断调整其它参数，固定一组参数不变：a1=0.6，a2=0.3，α1=0.5，α2=1.5，β1=0.5，v1=0.2，v2=0.3，c1=0.1，c2=0.1，绘制系统（7）关于β2的单参数分岔图，如图4（a）所示，图形的形状与图3 类似．从图中可以看出当参数0＜β2＜4.17时，系统是很稳定的，当系统处于稳定的区间，市场表现为稳定有序；当参数4.17＜β2＜4.22时，系统表现为混沌状态，当混沌现象发生时，市场就会进入到一种混乱无序的杂乱状态，在这种情况下，无论是厂商自己还是他们的竞争者都无法避免受混乱状态的影响，尤其对市场上的一些根基并不稳固的小厂家来说生存很是困难，市场的不稳定影响的就不只是市场了，整个社会都会受其影响，在这个时候，寡头厂商B 管理者应尽力控制产品替代率，尽量不要因为眼前利益就发动价格战，进而产生市场的混乱．图4（a）的最大Lyapunov 指数如图4（b）所示．

图4 系统（7）关于参数 2β的分岔图和相应最大Lyapunov 指数图Fig 4 Bifurcation Diagram and Corresponding Maximum Lyapunov Exponent Diagram about Parameters 2βof System (7)

3.3 边际成本c1和c2对系统稳定性的影响

接下来讨论寡头厂商A（B）的价格敏感系数c1（c2）对系统稳定性的影响．

图5 是系统寡头厂商商品售价p1和p2关于参数c1的分岔图和相应的最大Lyapunov 指数图．通过不断调整其它参数，取一组参数不变：a1=3 ，a2=3 ，α1=4 ，α2=4 ，β1=0.8，β2=0.8，v1=0.4，v2=0.4，c2=0.2，绘制系统（7）关于c1的单参数分岔图，如图5（a）所示．从图中可以看出当参数0＜c1＜0.21时，系统是很稳定的，当系统处于稳定的区间，市场也就稳定了；当参数0.21＜c1＜0.318时，系统处于混沌状态，在混沌状态下，市场也就变得混乱了，各厂商都会受其影响，这个时候厂商A 就应该控制敏感系数c1，避免市场发生混乱．图5（a）的最大Lyapunov 指数如图5（b）所示．

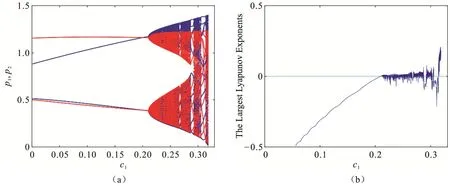
图5 系统（7）关于参数c1的分岔图和相应最大Lyapunov 指数图Fig 5 Bifurcation Diagram and Corresponding Maximum Lyapunov Exponent Diagram about Parametersc1of System (7)

图6 是系统寡头厂商商品售价p1和p2关于参数c2的分岔图和相应的最大Lyapunov 指数图．取其它参数不变：a1=3 ，a2=3 ，α1=4 ，α2=4 ，β1=0.8，β2=0.8，v1=0.4，v2=0.4，c1=0.2，图形的形状与图6 类似．

从图6 中可以看出，当参数0＜c2＜0.21时系统是很稳定的，当系统处于稳定的区间时，市场也处于稳定状态；当参数0.21＜c2＜0.318时，系统处于混沌状态，在混沌状态下，市场也就变得混乱了，各厂商都会受其影响，这个时候厂商B 就应该控制敏感系数c2，以避免市场发生混乱．图6（a）的最大Lyapunov 指数如图6（b）所示．

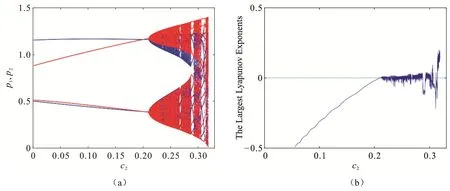
图6 系统（7）关于参数c2的分岔图和相应最大Lyapunov 指数图Fig 6 Bifurcation Diagram and Corresponding Maximum Lyapunov Exponent Diagram about Parametersc2of System (7)

3.4 对系统（7）混沌吸引子和相图的模拟

当参数v1的取值为4.5、4.4、4.3、4.2、4.1、4.0、3.9、3.8 时，系统（7）的吸引子和相图见图7．从图7 中得出，系统（7）表现混沌状态时，对应图（a）和图（b）中的混沌吸引子．

4 结 语

本文建立了一个寡头垄断博弈模型，分析了价格调整对寡头厂商利益以及整个市场的影响．数值模拟结果表明，一旦价格调整率超过稳定范围，整个市场将陷入混乱，寡头厂商自身利润也将减少．寡头垄断厂商或当前寡头垄断厂商应采取较低的价格调整率，以实现利润最大化．从上文可以得出，在寡头市场价格调整时会出现分岔甚至混沌现象，这对社会发展非常不利，有关部门应该规范市场，从而让市场和社会健康持续地发展下去．

所有寡头垄断者初始状态的微小差异都会对分析结果产生很大影响．为了稳定市场，寡头垄断者应慎重选择博弈的初始条件．当市场处于混乱状态时，寡头垄断者可以使用延迟反馈控制来控制混沌．

在有限的理论下，博弈模型是建立在销售量仅与价格有关的条件下，实际上影响销量的因素很多，如产品质量、市场需求等，这些问题需要进一步分析．

图7 系统（7）关于参数v1变化时的混沌吸引子、相图Fig 7 Chaotic Attractors and Phase Diagram about Parametersv1of System (7)