应用相似三角形的性质推证数学中的“并联”规律

◎秦宇峰

如果两个三角形相似，那么三边对应成比例，对应高之比等于对应边之比。物理在电路图中，若两个灯泡并联，一个电阻为R1，另一个电阻为R2，则有R总是R1、R2的调和平均数。其实在数学中，还有许多结论也符合并联规律。如：

1.已知：AB‖CD，AD、BC相交于E，过E作EF‖AB，交BD于F，AB=a，CD=b。求证：

总结：如果三条线段平行且构成如图的形状，那么中间线段是两边线段的调和平均数。

2.已知AB⊥BD，CD⊥BD，AD、BC交于点E，EF⊥BD，AB=a，CD=b。求证

证明：∵AB⊥BD，CD⊥BD，EF⊥BD，

∴AB‖CD‖EF

以下的证明过程同第一题。

总结：如果三条线段都垂直于同一条线段且构成如图的形状，那么中间线段是两边线段的调和平均数。

3.已知：在△ABC中，AD⊥BC，BC=a，AD=b，EFGH是正方形，E在AB上，H在AC上，FG在BC上，EH交AD于点M。求证

总结：在一个任意三角形中，如果它的内接正方形的一边在三角形的一边上，那么这个正方形的边长是三角形这一边与高的调和平均数。

4.已知：在Rt△ABC，AD⊥BC，∠BAC=90°，AB=a，AC=b，BC=c，EFGH是正方形，E在AB上，H在AC上，FG在BC上，EH与AD交于点M。求证

总结：在一个直角三角形中，如果它的内接正方形的一边在斜边上，那么这个正方形的边长等于三边之积与两直角边的积加上斜边的平方的和的商。

练习：

5.已知：在Rt△ABC，∠C=90°，BC=a，AC=b，D在AC上，E在AB上。求证

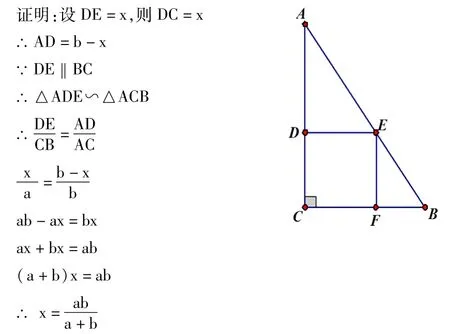
总结：在一个直角三角形中，如果它的内接正方形的两边在直角边上，那么这个正方形的边长是两直角边的调和平均数。

这些题的结论相同或接近，一条线段是另外两条线段的调和平均数。记住在什么条件下可以得到什么结论，非常有助于我们解题，可以缩短思维回路，尤其针对选择题或填空题，会起到意想不到的快捷与方便。