深度学习视角下高中数学教学策略
☉江苏省常熟外国语学校 马晓丹
现代教学理念认为,高中数学教学不但要注重问题解答的正确与否,而且也要促使学生理解问题解答过程中所蕴含的数学思想和方法,也就是说要关注学生在学习过程中的各种情感体验.而深度学习非常注重数学问题的来龙去脉和数学知识的内在逻辑意义,对于培养学生的发散思维、开发智力、积累数学活动经验、引导学生应用批判的眼光审视问题具有举足轻重的作用,因此,在高中数学教学中探究基于深度学习视角下的教学策略具有重要意义.
一、基于深度学习视角下高中数学教学策略
1.创设情境,弄懂“来龙”
为了帮助学生建立新旧知识之间的联系,促使学生掌握复杂的、深层次的非结构化知识,有效体现深度学习的关联性、连贯性等特点,教师应联系学生的生活、学习经验,结合原有学生的认知结构创设适当的教学情境,其中情境的创设要能引发学生的交流与思考,要有助于学生形成猜想和发现问题.
以引入“任意角的三角函数”为例,为能够有效激发学生的深度学习,笔者创设了如下现实生活中学生所熟悉的情境:要求学生观察汽车车轮旋转(前进、后腿)与里程表指针摆动之间的关系,然后启发学生思考,假设车轮半径为单位1,如何简化里程表的计算方法;假设任取车轮上的一个定点,如何描述该点相对于车轴的运动变化情况,从而帮助学生引出任意角、弧度制等教学内容.
2.注重反思,看透“本质”
在传统的课堂教学中,有相当一部分数量的学生仅是相关知识的记忆者,并没有从本质上理解为什么要这样解题,也较难接受一些新的观点,而在深度学习的视角下,教师应让学生应用批判的眼光审视新的问题,弄清数学问题的来龙去脉,并及时反思该类问题的结构、方法及证明的思维过程,反省此题与其他题目之间的联系与区别,也就是要准确把握数学问题的本质属性.
一是在涉及数学问题的探索、发现或者证明的过程中,实施心理接受式教学策略,即帮助学生从心理上接受问题的正确性.例如,在组织学生学习“等差数列前n项和”的知识时,如果只是将公式直接呈现给学生,那么只能导致学生机械记忆,如果应用“倒序相加法”推导出等差数列前n项和的公式,并通过证明的形式实施心理接受式教学策略,则更有利于学生记忆和理解,也能够提高学生分析问题和解决问题的能力.
二是鼓励学生从多个角度分析领悟内化数学问题中所蕴藏的内涵,教会学生应用批判的眼光感受命题的应用价值.
例如,在传统证明基本不等式的教学过程中,教师通常会采用构建指数函数、半圆、梯形等方式证明基本不等式,但为了帮助学生养成批判性地认识事物、学习知识,引导学生从直观图形中发现隐藏的基本不等式,笔者呈现了如下全新的证明方式.
已知⊙A、⊙B的直径分别为a、b,⊙A、⊙B相切,如图1所示,作出两圆的公切线CD,连接两圆的圆心AB,形成四边形ABDC,并且过点D作DE,使得AE=BD,所以,在Rt△DEC中,根据直角三角形中任意直角边小于斜边这个学生已经掌握的知识,从而引导学生总结得出基本不等式.

图1
3.挖掘本质,灵活“去脉”
为了达到灵活运用所学知识的目的,逐步加深理解所学知识,教师应鼓励学生将所学知识进行应用和推广,将所学的理论知识迁移运用到实践中去.
首先,实施强化策略,提高运用知识的熟练度及准确性,尽管关注解决问题所需要的公式及外在线索属于浅层次的教学策略,但对于知识的直接应用并不可省.例如,教师可以将焦点放在寻求解决问题的核心论点和概念上,适当拓宽命题的适用范围.
其次,实施变式策略,为了实现学生对于知识的迁移与知识的建构,教师应在学生的最近发展区内,引导学生在新的情境中对关键要素进行解读和判断.例如,在组织学生探究“余弦定理”时,为了防止学生形成思维定式,教师应将a2=b2+c2-2bccosA进行变形,从而得到
再次,实施发展性策略,即结合命题的形式特点,善于使用追问的策略,使学生处于“愤悱”的状态.例如,在“基本不等式”的教学中,由于两项、三项是成立的,笔者引导学生再次探究四项是否成立,如果是n项,上述结果还是否成立,在此过程中,逐渐引导学生实现深度学习,开发智力.
二、基于深度学习视角下的高中数学教学实践
仅有相关理论是不够的,而高中数学学习本身就是理论与实践相结合,因此,为了检测基于深度学习下的高中数学教学策略在实际应用中的有效性,笔者以“平面向量基本定理”为例进行了深入探究.
1.问题“来龙”
为了锻炼学生的逻辑思维能力,帮助学生得出本节课程所要探讨的核心问题,清楚、准确、简练地表达平面向量的基本定理,笔者通过以下问题串的形式进行复习引入:
(1)你能否正确叙述出向量共线定理.
(2)在平面内任一向量能否可以由一非零向量表示?是否可以用两个不共线的向量表示?
2.问题“实质”
为了帮助学生对平面向量基本定理产生内化的认知过程,引导学生结合图形感受实数对的唯一性,笔者设计了如下问题情境.
如图2所示,已知e1、e2是平面内两个不共线的向量,试求任一向量a能否用e1、e2来表示.

图2
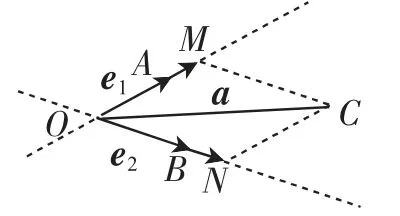
图3
然后,以小组为单位,探讨出e1、e2、a之间的关系,并通过平移的方式描绘出这三个向量的位置关系,如图3所示,要求学生再次观察上述图形,并引导学生联想向量线性运算中的平行四边形法则,思考能否应用平面内两个不共线的向量表示平面内的任意向量.在此基础上,通过直观图解、介绍正交分解等概念,进一步组织学生探究任一向量a与两个不共线的向量e1、e2之间的关系,总结出平面向量基本定理,共同验证“向量分解的唯一性”.
同时,为了进一步加深学生对概念的理解,有效体现“基本”的含义,教师还应通过追问的形式启发学生思考,促使深度学习.如平面向量基本定理中的基底e1、e2是否唯一?若基底选取不同,则表示同一向量的实数λ1、λ2是否相同?
3.问题“去脉”
为了体现数学在现实生活中的巨大价值,有效帮助学生建立起跨学科之间的联系,笔者结合所学知识,创设了如下物理情景:如图4所示,已知斜面与水平面的夹角为θ,某一质量为M的物体静止地放在斜面上,试求斜面对物体M的摩擦力f.
然后要求学生通过力的分解进一步体现平面向量基本定理的现实意义,思考向量共线定理与平面向量基本定理有什么区别与联系,能否举例说明平面向量基本定理在现实生活中还有哪些具体表现?并在此基础上猜想空间向量具有哪些性质?最后,通过如图5所示的网络结构帮助学生完善知识结构,感受平面向量基本定理的数学意义.
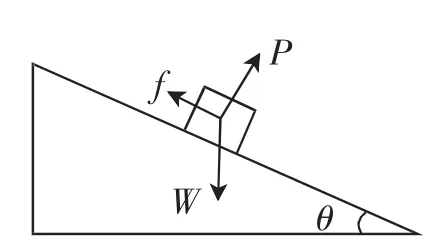
图4
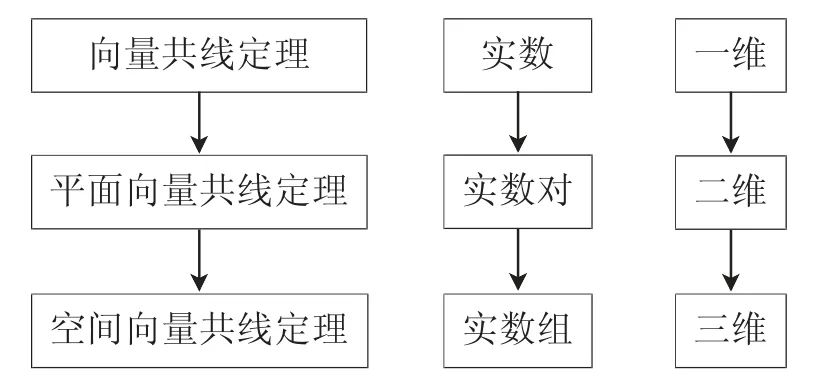
图5
综上所述,深度学习是实现核心素养落地的重要途径,在高中数学教学实践中,教师应结合学生已有的知识经验和生活实际,利用数学知识之间的内在联系,通过追问的形式充分挖掘问题的来龙去脉,促使学生在反思中看待问题、发展思维,只有这样,才能从本质上理解数学知识的内涵和外延,才能不断提高数学教学的质量与水平.

