例谈利用切线解决不等式问题

☉湖北省通山县第一中学 万小勇

导数在不等式中的应用是高考的热点，常见的命题角度有利用导数证明不等式和利用导数解决不等式恒成立中的参数的范围问题.对于这些问题的解决，一般采用分类讨论法或分离参数法.通过对大量相关试题的处理发现，有些题目处理起来比较烦琐，那么有没有其他的办法解决这类问题呢？下面通过例题谈谈利用切线的方式解决这类问题.

题型1：利用切线证明不等式

例1已知f（x）=ex（x+1），g（x）=-x2+2x+1.证明：f（x）≥g（x）.

图1

证明：显然f（x），g（x）都过点（0，1），考虑f（x），g（x）在（0，1）处的切线，对f（x）求得切线方程为y=2x+1，对g（x）求得切线方程为y=2x+1，要证f（x）≥g（x），不妨证明f（x）≥2x+1≥g（x），先证明f（x）≥2x+1，记h（x）=ex（x+1）-2x-1，则h′（x）=ex（x+2）-2.

当x＞0时，ex＞1，x+2＞2，所以h′（x）＞0；

当x＜0时，ex（x+2）＜2ex＜2，所以h′（x）＜0.

所以h（x）在（-∞，0）上递减，在（0，+∞）上递增.

所以h（x）≥h（0）=0，即ex（x+1）≥2x+1.

再证明2x+1≥g（x），令t（x）=（2x+1）-（-x2+2x+1）=x2≥0.

上式恒成立，所以ex（x+1）≥2x+1≥-x2+2x+1.所以f（x）≥g（x）.

题型2：利用不等式中的一次函数特征，直接考虑转化为曲线在某点处的切线，解决不等式问题

例2设函数f（x）=ex-e-x，若∀x∈［0，+∞），恒有f（x）≥ax成立，求实数a的取值范围.

图2

分析：对于此题可以考虑构造函数g（x）=f（x）-ax，求g（x）min≥0，显然需要分类讨论，当然也可以通过分离参数来解决，但如果我们注意到f（x）=ex-e-x≥ax（x≥0）的几何意义是：曲线y=ex-e-x（x≥0）恒在射线y=ax（x≥0）的上方，那么就可以考虑利用切线为界线来处理.

解：因为f′（x）=ex+e-x，则f（x）在x=0处的切线方程为y=2x.

易证f（x）≥2x（x≥0）恒成立，则要f（x）≥ax成立，只需f（x）≥2x≥ax成立，所以a≤2.

题型3：通过构造一次函数，进而考虑曲线在某点处的切线来解决不等式问题

例3已知函数f（x）=sinx-xcosx（x≥0），若∀x∈［0，+∞），不等式f（x）≤ax3恒成立，求实数a的取值范围.

解析：因为f（x）=sinx-xcosx（x≥0），又由f（x）≤ax3得所以记则g（x）≤ax的几何意义为g（x）对应的曲线恒在射线y=ax（x＞0）下方.考虑g（x）在x=0处的切线.

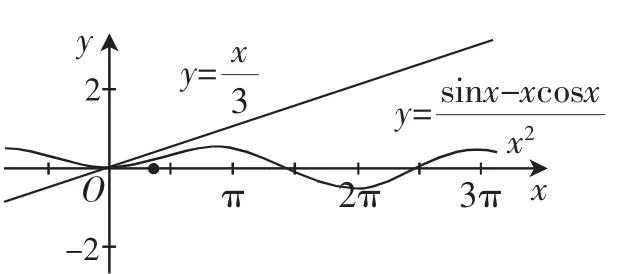
图3

由上观之，在上述问题的处理中，考虑以切线为临界位置，不等式左右两侧对应的曲线以切线为界，借助于切线，从而使问题变得简洁，为我们处理不等式证明或利用不等式恒成立解决参数问题提供了一个不错的思路.

【回顾高考】

利用这种解题策略来看看在高考函数与导数题中如何应用.

题1（2017年全国卷Ⅱ，文）设函数f（x）=（1-x2）ex.

（1）讨论f（x）单调性；

（2）当x≥0时，f（x）≤ax+1，求a的取值范围.

解析：（1）略.

（2）考虑f（x）在x=0处的切线，因为f′（x）=ex（-x2-2x+1），所以f′（0）=1.所以f（x）在x=0处的切线方程为x-y+1=0.

由图像（图4）知f（x）≤x+1，接下来证明这个不等式.记h（x）=ex（1-x2）-x-1，则h′（x）=ex（-x2-2x+1）-1，令t（x）=ex（-x2-2x+1）-1，则t′（x）=ex（-x2-4x-1）＜0，所以t（x）在［0，+∞）上单调递减，所以t（x）≤t（0）=0，所以h′（x）≤0，所以h（x）在［0，+∞）上单调递减.所以h（x）≤h（0）=0.所以ex（1-x2）≤x+1.所以要使f（x）≤ax+1恒成立，显然只需x+1≤ax+1恒成立.所以a≥1.

图4

题2（2008年全国卷Ⅱ）设函数

（1）求f（x）的单调区间；

（2）如果对任意x≥0都有f（x）≤kx，求实数k的范围.

解析：（1）略.

故当x∈［0，arccos3k）时，h′（x）>0，因此h（x）在［0，arccos3k）上单调递增.

当x∈（0，arccos3k）时，h（x）>h（0）=0，即sinx>3kx.