重要不等式变式的推广及应用*
2019-10-11 05:48四川内江师范学院数学与信息科学学院杨诗棋
中学数学杂志 2019年19期
☉四川内江师范学院数学与信息科学学院 杨诗棋
☉四川内江师范学院数学与信息科学学院 宋元妹
☉四川内江师范学院数学与信息科学学院 刘成龙
(a-b)2≥0是中学阶段最基本、最重要的不等式.由(a-b)2≥0出发可以得到一系列变式,比如[1]:等.这些变式应用广泛,是证明分式不等式的一把利剑.当然,这些变式也存在一些局限:证明的对象仅仅限于一次或二次.为突破次数的限制,有必要对这些变式进一步“升级”.文中仅对进行推广,并运用推广处理一些不等式的证明,以此抛砖引玉.
一、变式的推广
推广:设a,b∈R+,n∈N且n≥2,则,当且仅当2a=b时取等号.
证 明:则(2a)n≥2nabn-1-(n-1)bn,两边同除2nbn-1可得
二、推广的应用
例1(美国《大学数学杂志》1991年第4期征解题)设xi∈R+(i=1,2,…,n),求证xn(x1+x2+…+xn-1+xn).
证明:原问题等价于xn-1+xn,
当且仅当x1=x2=…=xn时等号成立.


当且仅当a1=a2=…=an时等号成立.
例3设ai,bi∈R+,i=1,2,…,n,n∈N*,且,求证
证明:原问题等价于
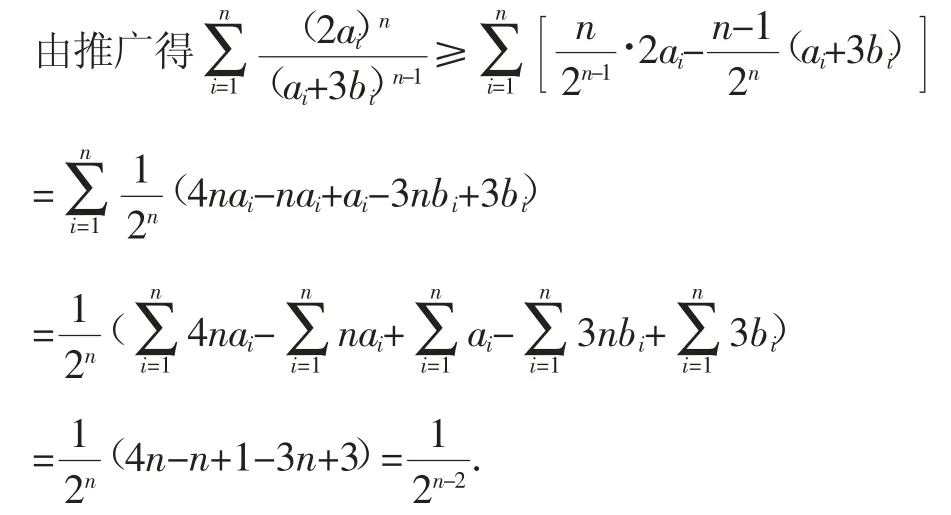
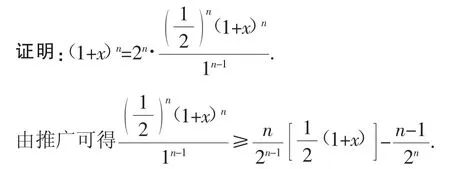
例4(伯努利不等式)x>-1,n为正整数,则(1+x)n≥1+nx.
例5(权方和不等式)设ai,bi>0,i=1,2,…,n,k∈R+,则
证明:令s=(a1+a2+…+an)-1,t=(b1+b2+…+bn)-1,则原不等式等价于

猜你喜欢
教育实践与研究(2022年18期)2022-10-21
山西大同大学学报(自然科学版)(2022年1期)2022-03-17
科教创新与实践(2021年27期)2021-09-22
今日农业(2020年18期)2020-12-14
中学数学研究(江西)(2020年7期)2020-07-22
数学大世界(2020年5期)2020-06-22
中学生数理化·七年级数学人教版(2018年12期)2019-01-31
东方教育(2017年7期)2017-07-03
中国信息技术教育(2015年18期)2015-11-03
当代县域经济(2015年12期)2015-03-20

