如何在解题教学中渗透学法指导

☉江苏省江阴高级中学 沈敏忠

很多高中学生都会为自己的数学学习准备几本好的资料，将资料上的练习题做上一遍就可以提高数学成绩是这部分学生的普遍认知，然而这种认知和行为却往往不能为其带去良好的学习效果，实际上，将大量的时间和精力置于盲目解题却又不反思、总结的行为并不能令其数学成绩得到有效提升.

笔者结合自己的教学实践、高中数学的学科特点进行了学习方法渗透的研究与思考，具体做法如下.

一、培养学生独立思考的习惯

重视学生主体并培养学生独立思考的习惯能够有效促进学生的积极参与和认知结构的完善，学生静心思考和独立解题能够有效地增强其数学学习的自信.

例1已知α，β∈，且，求证：

分析：学生在解决此题时，如果不能对题目进行独立的思考和分析，在答题时不假思索地运用常规思路求解sin（α+β）或cos（α+β），并结合α+β的取值范围进行证明，但题中的条件等式只有一个，从而求解三角函数值是行不通的，解题受阻自然产生.因此，变换思维角度来求解是必须的，先证α+β≥，再证α+β≤，或者运用反证法令问题得解.

证法1：首先，由已知等式得sin2α+sin2β=4sinαsinβ，即sin（α+β）cos（α-β）=cos（α-β）-cos（α+β），cos（α+β）=cos（α-β）［1-sin（α+β）］≥0.因为α+β∈（0，π），所以α+β≤；其次，由已知等式及均值不等式可得所以cotαcotβ≤1，即tanαtanβ≥1.所以又因为，所以α≥，即α+β≥综上可得

证法2（反证法）：因为，所以α+β∈（0，π）.设，若，则，由正、余弦函数的单调性可得，所以，与已知矛盾.同理可证，当＜α+β＜π时，与已知同样矛盾.因为α+β∈（0，π），所以

这一道有一定难度的题目的解题教学不仅对反证法的解题思路进行了巧妙的复习，还使学生在新问题的独立思考中获得了分析问题、解决问题的能力.学生养成独立思考习惯的同时也大大提升了自身的数学素养.

二、培养学生一题多解、多解归一的思考意识和习惯

引导学生在解题中进行一题多解、多解归一的思考能够有效地发展学生的智力和解题能力，学生的数学学习变得生动活泼的同时也大大减少了题海练习，数学学习的视野也会因此更加开阔.从不同方向对同一道数学题进行审视往往能够得到不同的解法，因此，教师在解题教学中应抓住一切有利时机对学生进行有针对性的启发，使学生在已有知识的基础上尽可能地提出各种不同的新构想，使学生能够逐步养成追求更好、更简、更巧的解题方法的意识与习惯，基础知识之间的纵横联系与沟通也因此变得更为紧密，学生也会在解题能力发展的同时获得更为广阔的解题思路.

例2已知f（x）=，a，b为相异实数，求证：|f（a）-f（b）|＜|a-b|.

从探求解题方法的角度对这道不等式证明题进行思考可以获得以下思路：

思路1：常规方法，首先进行平方，将绝对值符号去掉，然后作差比较，最后运用配方法进行证明.

思路2：作商比较法，首先运用共轭根式的知识将分子进行有理化，然后利用放缩原理进行证明.

思路3：三角代换法，观察式子的结构特征并联想函数，令x=tanα，然后再转化成三角不等式进行证明.

思路4：构造复数证明，结合函数的特点，以及复数的模构造复数z=1+xi，然后利用复数的三角不等式进行证明.

思路5：考察表达式f（x）=可视作点P（x，1）到点O（0，0）的距离，当a≠b时，由点P1（a，1）、P2（b，1）与原点确定的△OP1P2中任一边大于其余两边之差即可令问题得到证明.

思路6：解几证法，方程f（x）=表示双曲线y2-x2=1的上支，为双曲线上两点（a，f（a））、（b，f（b））连线的斜率的绝对值，则问题即转化为估计双曲线的上支的任一弦所在直线的斜率，双曲线y2-x2=1的渐近线斜率是±1，则得证.

解决本题可以从代数和几何两个角度入手，引导学生联想一题多解模式并使学生学会从多角度观察、思考和联想，能使学生在已有知识的基础上进行融会贯通并获得更多的解题办法.符合学生认知心理与认知规律的这种引导不是解题方法的简单罗列，也不是解题思路的强行灌输，而是引导学生自主探索、自我发现的有益思维过程.

三、培养学生及时小结和纠错的习惯

各种原因都可能导致学生在解题时出错，错误自然在所难免，但一错再错的现象却值得教师关注，这是学生混淆概念、忽视隐含条件、特殊代替一般、忽视特例、逻辑不够严密等问题造成的，因此教师应该在教学中对学生不断地进行针对性的训练和培养，使学生能够逐步养成及时小结和纠错的习惯，并因此达成有效防范错误的目的.

例3若是第二象限的角，则m的取值范围为（ ）.

A.m=8 B.3＜m＜9

C.m=0或m=8 D.-5＜m＜9

错解：θ是第二象限的角，由和-1＜解得3＜m＜9，故选B.

这是一个典型错误，其实只要在解题后对其进行检验，很快就能发现这一解答是错误的.取m=5，则sinθ=此时.这是没有考虑sin2θ+cos2θ=1这一隐含条件而导致的错误，本题应选A.

合理“设置错误”以帮助学生及时发现错误和纠正错误也是极有意义的教学手段，这能使学生在错误的发现、辨析和纠正中抓住问题的本质，使学生能够对问题形成全方位、多角度的思考和分析并获得事半功倍的学习效果.不仅如此，学生还能因此逐步养成不断反思的好习惯.

四、培养学生写“数学小论文”的习惯

很多数学概念与结论都给人特别抽象的感觉，但事实上，很多数学问题都是从现实生产、生活中得来的.教师应使学生能够明白这种意义并运用已有知识解决超出教材范围的问题.

例4一扇形铁板AOB的半径是R，圆心角是，在该扇形中切割下一内接矩形PQRS，矩形PQRS的各顶点均在扇形的弧或半径上，则该矩形的最大面积是多少？

分析：解决本题首先应弄清楚内接矩形有如图1、图2所示的两种情况并分别作出处理，再最终求出其最值.由题意可知，首先可以构造函数，然后选取如图所示的自变量θ并建立矩形面积关于θ的三角函数.图1中矩形的面积很快可以求出，面积，可得当时，其面积可取最大值；图2中矩形面积可得当时，其面积取得最大值.因为，因此如图1所示的内接矩形的最大面积更大，为这一结论得出之后，教师应该启发学生进行以下思考：条件发生变化时可得出什么结论呢？你在这一结论中可得到什么启示？引导学生首先提出问题并在此基础上进行数学小论文的创作.

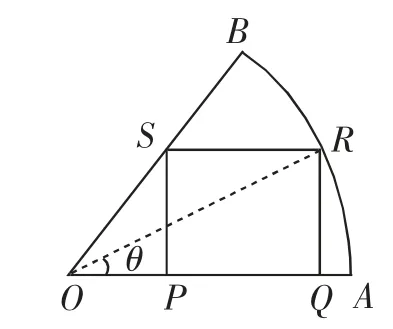
图1

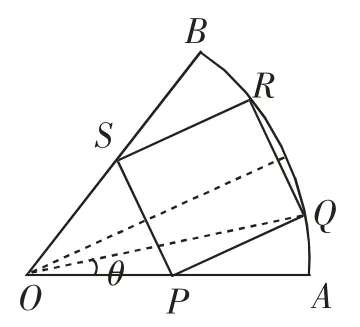
图2

总之，教师应对教与学这一双边活动进行更多的思考，将学法指导渗透进教学的各个环节中去并因此促成学生更多的领悟思考，使学生能够在掌握更多学习方法的过程中获得更多终身受益的能力的领会和提升.