基于直观想象的数学高考*
——以2019年全国高考数学选择题为例
☉重庆市永川中学 盘如春
☉北京师范大学教师教育研究中心 桑国元
☉北京师范大学数学科学学院 曹一鸣
一年一度的普通高考刚刚结束,今年的高考数学试题到底怎么样呢?是否达到了有利于高校选拔人才、有利于在中学数学教育教学中激发学生学习数学的热情,提高对数学价值的认识,提升数学素养,对中学的素质教育有很好的导向和促进作用.作为一名数学教育工作者,应该认真思考、及时总结.
我们一线的教师都还记得,2018年8月,教育部考试中心主任姜钢、党委书记刘桔,在《中国教育报》发表署名文章——《牢记立德树人使命,写好教育考试奋进之笔》.文章的核心观点是:要用党的十九大精神统领高考命题工作,全面落实立德树人要求.这是对2019年高考命题的“最新定调”和顶层设计.“新定调”对高考命题工作具有非常重要的指导作用,对考生的备考更具有方向性的指引.
由此我们认为,高考命题要坚定正确的政治方向,紧紧围绕高考的核心功能,上好“立德树人一堂课”、做精“服务选才一把尺”、树好“引导教学一面旗”,做到科学设计考试内容,优化高考选拔功能,强化能力立意与素养导向.各学科命题都要体现十九大的新精神、新论述,体现高考的“加强社会主义核心价值体系教育”和“增强学生社会责任感”的育人功能和政治使命,并坚持把创新思维和学习能力考查渗透到命题全过程,落实“重思维、重应用、重创新”的命题要求,使高考由“解答试题”转向“解决问题”.
高考是个宏大、系统的工程,命题是一个专业、精致的系统,今年的高考是如何在“新定调”的基础上,落实“重思维、重应用、重创新”的呢.现结合《普通高中数学课程标准(2017年版)》(以下简称《标准》),本文仅从“直观想象”核心素养的维度来分析、解读,以期抛砖引玉.
直观,是指通过对客观事物的直接接触而获得的感性认识.直观想象是指借助几何直观和空间想象感知事物的形态与变化,利用图形理解和解决数学问题的过程.这也正是《标准》中对直观想象核心素养的定义.在“初、高中数学直观性教学的差异性研究”一文中,我们对直观想象作了更进一步的研究,认为直观不仅可以从几何图形这一显性符号处获取研究对象,还可以从更一般的、抽象的数学符号处获取研究对象,正如当我们看到π就想到圆周率,看到就想到积分一样,这显然也是一种直观,只是相对于图形直观而言,这是一种更高级、更抽象的直观.为此,继续借“初、高中数学直观性教学的差异性研究”一文的研究成果,从图形直观、符号直观、情境直观、模型直观的角度来解读直观想象这一核心素养在今年高考试题中的呈现方式.
一、图形直观
题1(全国卷Ⅰ理科4)古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是,著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是若某人满足上述两个黄金分割比例,且腿长为105cm,头顶至脖子下端的长度为26cm,则其身高可能是( ).
A.165cm B.175cm C.185cm D.190cm
此题有强烈的实物情境,在试卷中,已给出了实物图,如何从图中所给出的众多数据中,快速、准确地找出各数据间的关系,是解决此题的关键.为此,可以试着由问题的叙述,画出示意图,借用图形直观来表达数学问题.
如图1所示,设头顶、咽喉、肚脐、足底分别对应点A,B,C,D,身高为x,故考虑到题中还有条件,腿长为105cm,头顶至脖子下端的长度为26cm,由于要估计身高,这就要建立一个与身高的关系.通过图形,可以直观地看到,肚脐与腿间还有一段距离,咽喉与脖子下端还一段距离,如何利用这两段未知的距离来估计身高,这是问题的关键.

图1
由图1可知,AB<26,CD>105.
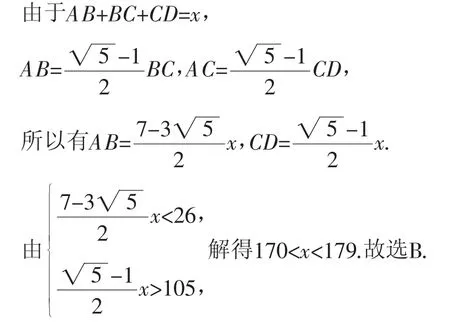
当然,有的学生以生活经验,参照日常接触的人,直接选B,这姑且算作是直觉吧,需另当别论.
在高中学习阶段,由于学生的心智水平与学识所限,学生的思维常以图形直观为主,借助图形直观认识事物的位置关系、形态变化与运动规律,再利用图形描述,分析数学问题,建立形与数的联系.为此,教师要善于利用学生的这一认知规律,以图形直观为突破口,充分发展学生的理性思维,提升学生解决问题的能力.这正是图形直观的作用所在.
二、符号直观
题2(全国卷Ⅱ理科4)2019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆,我国航天事业取得又一重大成就,实现月球背面软着陆需要解决的一个关键技术问题是地面与探测器的通讯联系.为解决这个问题,发射了嫦娥四号中继星“鹊桥”,鹊桥沿着围绕地月拉格朗日L2点的轨道运行.L2点是平衡点,位于地月连线的延长线上.设地球质量为M1,月球质量为M2,地月距离为R,L2点到月球的距离为r,根据牛顿运动定律和万有引力定律,r满足方程:设,由于α的值很小,因此在近似计算中,则r的近似值为( ).
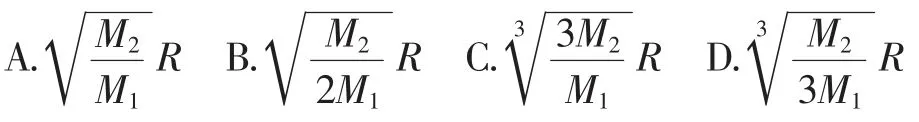
此题正如许多考生的评论,怀疑自己是否拿错了试卷,这分明是一道物理试题怎么出现在数学试卷中?但我们稍加思考会发现,此题仅借用物理知识这一背景,试题的解答与物理知识没有任何关系.注意到题中的条件与结论都与α这一符号无关,但题中又引入了这一符号,在这一符号直观的启发下,我们自然联想到先将条件化为关于α的关系,再做计算,得到如下的解答.
数学直观是一种相对的直观,对于还未掌握的概念而言,已经掌握的概念就是直观的.数学符号也是如此.希尔伯特就曾经说过“符号本身就是数学思考的对象”.布鲁纳也认为:“数学中的符号使得原理的创造及数学体系的扩充成为可能”.符号是目前人类对知识最有效,同时也是最强力的压缩和加工方式.
本题正是在符号直观的引领下,兼顾条件与结论,对问题进行计算推理,最终解决问题,从而在高考中体现考查直观想象这一核心素养.在教学中,教师不能仅从核心素养的条文或原则出发,空洞地大谈核心素养,而是要在领会核心素养本质的基础上,在教学中,细化核心素养的各要素,找到落实核心素养各要素的途径与方法.
三、情境直观
题3(全国卷Ⅱ理科12)设函数f(x)的定义域为R,满足f(x+1)=2f(x),且当x∈(0,1]时,f(x)=x(x-1).若对任意x∈(-∞,m],都有f(x),则m的取值范围是( ).
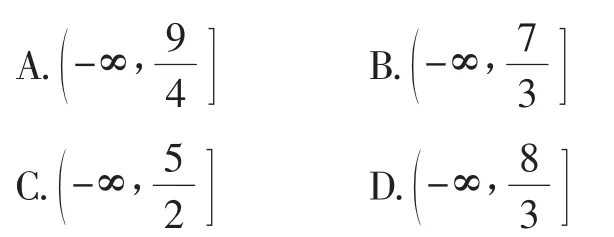
有同学拿到这个题不知从何入手,究其原因是对条件f(x+1)=2f(x)不知如何用?当然更深层的原因是对条件f(x+1)=2f(x)表达的意义不明白.
但同学们对f(x+1)=f(x)这一情境是明白的,它是一个周期函数,并且周期T=1,此时我们就要借用这一知识情境,思考如何处理f(x)前面多一个倍数2的问题.这样f(x+1)=2f(x)就可以直观地理解为后一段函数图像上点的纵坐标是前一段函数图像上相应点纵坐标的2倍,即函数图像每向右移动一个单位,所得图像的纵坐标扩大至原来的2倍,作出函数图像,借助图形直观,可求得m的取值范围.
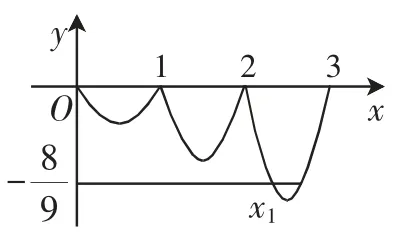
图2
根据第三段与x轴交点的横坐标是2,3,得第三段的解析式f(x)=4(x-2)(x-3).
在这一解题过程中,用到了直观想象中的多种直观,情境直观(由f(x+1)=2f(x)得出函数的特征是“周期类”函数这一知识情境,并在这一情境直观的启示下,作出这一“周期类”函数的图像),图形直观,从而顺利解决此题.这也体现了“直观想象是发现和提出数学问题、分析和解决数学问题的重要手段,是探索和形成论证思路、进行数学推理、构建抽象结构的思维基础”.
四、模型直观

图3
题4(全国卷Ⅰ理科6)我国古代典籍《周易》用“卦”描述万物的变化.每一“重卦”由从下到上排列的6个爻组成,爻分为阳爻“——”和阴爻“——”,如图3就是一重卦.在所有重卦中随机取一重卦,则该重卦恰有3个阳爻的概率是( ).

此题在中学数学学习中是常见的一类“模型”问题,即古典概型问题.之所以说它是一类“模型”,就是我们已经有了解决此类“模型”问题的基本经验和策略,学生只需要把所求问题转化为已有经验的数学“模型”,在原有模型直观的认知引导下,按已有解题经验或策略求解即可.
这就是我们所说的模型直观,这是一个学习者最为重要的一种学习方式,学习就是既要学,又要习.学就是模仿,在模仿中建立起解决此类问题的一种心理图式,即学得的经验;习就是在新的问题情境中,通过模型识别,寻找已学得模型对应的经验,解决问题.当然这里的习不是对原有模型简单的重复,而是一种再加工、再创造,唯有这样,一个学习者才能不断成长,突破模型,建立新的模型,走向创新.这正体现了高考“重思维、重应用、重创新”的考查目的.
分析、研究高考试题,是我们每一位一线教师应该做的基本工作.通过分析、研究高考试题,不仅能帮助我们一线教师把握高考动向,服务于考生,做好自己的本职工作,提升成绩,更重要的是研究高考试题背后所蕴涵的信息,如学科本质、核心素养、人文精神、价值取向等,唯有如此,教师才能以更高的视角、更理性的态度、更专业的方法,肩负起为中华民族伟大复兴培养人才的光荣使命.

