航空专用离心喷头雾化性能试验与影响因子研究

杨风波 薛新宇 蔡 晨 周晴晴 孙 竹

(农业农村部南京农业机械化研究所， 南京 210014)

0 引言

多旋翼植保无人机喷雾作业过程中，药液雾滴是在旋翼下洗气流、飞行迎风气流及自然风等耦合风场胁迫下输运到作物冠层，多旋翼植保无人机依靠旋翼的强大下洗气流将雾滴吹送到作物冠层，助力雾滴穿透稠密的作物冠层也促使叶片翻动，提高叶片附着率[1-3]；航空植保作业过程中飞行迎风气流和自然风迫使雾滴运动轨迹变化，产生药液雾滴飘移、并导致沉积均匀性降低，且出现了使得航线偏离的航空施药领域典型性问题[4-6]。目前，精准施药正在快速发展[7]，科研工作者应明确喷头喷雾参数和雾化性能参数之间的耦合关系，为制定合理作业方案、规划合理作业线路、减小雾滴飘移，提出精准作业方案提供有力支撑。

FORD等[8]研究了单个雾滴的杀伤范围，证明了单个雾滴都有其药效控制领域范围，这个范围称为杀伤面积或者杀伤半径，这个研究成果彻底否定了大容量的喷雾方式。WASHINGTON[9]在研究百菌清和代森锰锌对香蕉夜斑菌的防治效果时，发现雾滴体积中径(VMD)为250 μm时，百菌清雾滴杀伤半径为1.02 mm，通过控制雾滴中径，进而实现喷雾覆盖密度的联动变化，可以获得病、虫、草害的最佳防治粒径[10]。研究表明雾滴粒径和防治效果、防治范围直接相关，也说明了量化喷雾参数和粒径之间关系的重要性。而离心雾化喷头雾滴谱较窄，雾滴粒径易控制且不易堵塞喷孔，在航空植保低空低量施药模式下应用前景广阔[11-13]。鉴于此，本文针对航空专用离心喷头，研究喷雾参数与关键雾化参数的关系。

笔者在文献[14-15]中针对SLK-5六旋翼植保无人机建立了施药飘移预测模型，研究了前飞气流速度、下洗气流、雾滴粒径等因素对雾滴运动规律的影响，受当时研究条件限制，统一了喷头的工作参数，但并未展开详细研究。在田间实际作业过程中喷头的喷雾参数和雾滴粒径、初速度等直接相关，鉴于此，本文探索喷雾参数影响下航空专用离心喷头的粒径参数Dv50及喷幅，为后期四旋翼植保无人机施药飘移、沉积预测研究提供各喷雾参数下对应的雾滴初始属性。

1 航空专用离心喷头喷雾试验

1.1 离心喷头喷雾系统参数标定

CN1215型航空专用离心喷头如图1所示，包括离心驱动电机、喷盘及喷管。离心驱动电机的驱动轴固定在喷盘上以驱动喷盘转动，离心驱动电机的驱动轴为中空管轴，中空管轴的一端与喷盘的流道相通，中空管轴的另一端与喷管相连通；喷盘上具有多条流道，每条流道以喷盘的中心点为转动中心相对于径向方向偏移预定角度，并且每条流道呈弧形曲线；喷盘上的每个流道出口处均设置三角形尖齿，以克服雾滴粘性力，雾滴能被顺利甩出。先打开供液系统供液，待液流入喷头后，开启喷头供电系统，经过雾化后，雾滴群经过弧形曲线流道被甩出，如图1所示。

图1 CN1215型航空专用离心喷头Fig.1 CN1215 aviation special centrifugal nozzle

喷雾试验台由供液系统、支撑台架、升降杆(高度0.6～1.5 m范围内可调)和横杆(伸出长度0.5～1.6 m可调)组成。其中，供液系统由4路小型离心泵(额定电压12 V，最大流量400 mL/min，测试时只开启1路供液，如图2所示)、直流稳压电源(型号为QJ-3005S Ⅲ，电压可调范围0～30 V，电流测量范围0～3 A，如图3所示)、压力计(量程0～1 MPa)、水池和软管组成。

图2 供液系统离心泵Fig.2 Liquid supply system centrifugal pump

图3 直流稳压电源Fig.3 DC regulated power supply

雾滴粒径测试系统由激光粒度分析仪(型号：DP-02，测量范围0.1～1 500 μm，珠海欧美克仪器有限公司)、植保专用风洞及激光粒度分析系统组成。植保专用风洞内部提供封闭的无风扰动环境，激光粒度仪根据光的散射原理对雾滴进行测试，最后，激光粒度分析系统进行统计分析推算雾滴颗粒的大小。输出以下测试结果：遮光比、粒度特征参数(Sauter平均直径SMD、Dv50、边界粒径Dv10、Dv90)、粒度微分分布图和累积分布图。本文只取Dv50，为后期四旋翼植保无人机施药飘移、沉积数值计算提供喷雾初始边界。

工作过程中，喷雾系统的工作参数直接影响喷雾参数(供液流量及喷头转速)。针对离心泵供液流量、喷头转速这两个试验参数，展开喷雾系统工作参数标定，确定试验参数下对应的离心泵转速、喷头供电电压，为后续测试试验打下基础。根据试验设计方案，标定了18组工况下的系统工作参数，系统工作参数标定结果如表1所示。考虑实际情况，离心泵转速单位精确到1 r/min，喷头供电电压精确到0.1 V。

1.2 离心喷头喷雾参数测试

CN1215型离心喷头的Dv50测试方案如图4所示，制作了铝合金升降支撑平台，该平台上下、前后、左右6个自由度可调，将DP-02型激光粒度分析仪安装在铝合金升降支撑平台安装面上，方便后期的调姿对中。在NJS-1型植保直流闭口式风洞相对的两扇玻璃窗口上钻一对平行的孔，调节激光粒度仪的位姿，使得激光粒度仪的发送、接收端口均与植保专用风洞玻璃窗开孔处平齐并相互对中。将激光粒度仪打开并预热15 min，打开雾滴粒径测试软件，将系统自动对中调节，使背景光在0环的光柱最高，第1环高度小于0环的1/4，到12 环光柱高度依次降低；滤除背景光，按照表1的18个测试方案进行供液流量及喷头转速调试后，开始喷雾，等雾形稳定之后进行测量，系统测量、统计完成之后停止喷雾，测量获得雾滴平均微分分布，最后根据本文的研究目的，只取Dv50。

表1 喷雾系统参数标定Tab.1 Spray system parameter calibration

图4 雾滴粒径测试方案Fig.4 Droplet size measurement scheme

离心喷头喷幅测试方案如图5所示。喷头离地高度0.8 m，在喷头下方8个方向上(东、东南、南、西南、西、西北、北、东北)分别布置雾滴收集盒，离心喷头在无风条件下沉降区的中心部位无雾滴，所以中心区没有布置雾滴收集盒，鉴于雾滴收集称量任务较多，采用9.3 cm×9.3 cm的方形塑料盒；另外，该型离心喷头在沉降区雾滴分布并不是完全均匀的，所以喷幅(Dv50对应值)最终称量后取8个方向的平均值为准。按照表1的18个测试方案编号进行供液流量及喷头转速调试，在实验室内无风条件下进行喷雾，喷雾10 min后，停止。用干毛巾、布料擦拭雾滴收集盒，然后称取每个雾滴收集盒内雾滴质量，根据每个方向的雾滴量分布情况，以喷头的铅垂点为圆心，计算Dv50对应的喷幅距离(即沉积量累计为该方向的50%)，最后每组工况取8个方向喷幅的均值。18个工况Dv50对应的喷幅如表2所示。

图5 对应喷幅测试方案Fig.5 Corresponding spray amplitude test scheme

编号离心泵供液流量/(mL·min-1)喷头转速/(r·min-1)体积中径DV50/μm对应喷幅/cm1100800011739.6182100900010941.85031001000010540.9204150800013339.5255150900012141.10661501000011339.9907200800013043.8038200900011844.73392001000011143.24510250800012844.26811250900012244.640122501000011742.96613300800012946.31414300900012048.546153001000011248.17416350800012349.75517350900011850.127183501000011548.825

2 代理数学模型建模方法

代理模型是通过数学模型逼近输入变量与响应变量的方法[16]。而根据逼近输入、输出变量函数形式的不同，数学模型建立方法主要有响应面法、Kriging函数法、神经网络法等，综合建模效率及应用范围，神经网络均具有优势，该方法既有较高的建模拟合效率，也具有更广的应用领域，更适合实际工程问题的建模[17-18]。

2.1 响应面模型

响应面(RSM)模型是最常用的近似模型，目前，应用较多的RSM模型有二阶[19]、三阶[20]、四阶模型[21]；一般来讲,二阶、三阶、四阶模型中四阶的精度最高[21]。

采用四阶RSM构造近似数学模型，不考虑三次及以上交叉项[22]，其函数构造形式为

(1)

式中n——设计变量个数

a0、ai、aii、aiii、aiiii、aij分别为常数项、一次项、二次项、三次项、四次项、二次交叉项系数。

在式(1)中，各项系数通过最小二乘回归分析求解，使得样本值与预测值误差平方和最小，则四阶响应面系数向量可表述为

a=(xTx)-1xTF

(2)

式中，x是c维样本空间设计变量向量，x=(x1,x2, …,xc)T，且有x∈Rc。

2.2 Kriging模型

本文以普通克里金(Kriging)模型插值方法为例来说明Kriging插值的过程[23-24]。

样本点的估计表达式为

(3)

只要得到了加权系数W=(w(1),w(2),…,w(n))的表达式，就可以得到参数空间中的任意样本设计点y的估计值。Kriging模型的重要假设是将未知函数视为一个随机过程，该随机过程可以表示为

y(x)=f(β,x)+H(x)

(4)

式中f——全局趋势模型β——回归系数

H——随机分布的误差

将随机过程的方差记为σ2，可用协方差描述不同位置点随机变量的相关性，其协方差可描述为

Cov(H(xc),H(xd))=σ2Z(xc,xd)

(5)

式中，xc、xd为设计变量空间任意两个输入，Z为相关函数(只与空间距离相关)，有线性函数、指数函数、三次样条函数、高斯函数等多种形式。基于上述假设，Kriging模型寻找最优加权系数W，使得均方差最小，并且满足无偏差条件。鉴于本文影响因数与目标函数非线性关系较强，采用指数函数及高斯函数作为相关函数。

2.3 神经网络模型

2.3.1模型结构

和径向基神经网络(Radial basis function neural network，RBFNN)[25-27]一样，椭球基神经网络(Ellipsoidal basis function neural network，EBFNN)是一种可靠的前馈式神经网络方法[28]，也是高斯径向基神经网络的推广[29]。椭球基神经网络采用全协方差矩阵代替径向基神经网络中的对角型协方差矩阵，显著提升了网络的分类处理能力。神经网络是由输入层、隐层和输出层组建的3层前馈网络，其中输入层主要负责接收自变量，隐层负责对输入变量进行变换，输出层负责输出应变量，神经网络的最终输出是将几个隐节点的输出进行线性加权得到的[30-31]。

c维样本空间设计变量向量x直接被输入到隐层各个节点中，则隐层第k个EBFNN节点的激活函数(基函数)为

(6)

式中，ck=(ck1,ck2, …,ckc)T∈Rd和Σk=(σst)c(s,t=1,2,…,c)分别是第k个隐层基函数节点的均值向量和全协方差矩阵，γk是用来控制第k个隐层基函数离散度的平滑参数。

而隐层基函数参数ck、Σk平均算法和样本协方差由估计得出，即

(7)

(8)

式中Ωk——第k类训练样本矢量集

nk——Ω中的矢量数目，k=1, 2, …,K

输出层Yj(x)的第j个节点关于输入向量x的函数形式为

(9)

式中Sj 0——偏差项

Sjk——连接第k个隐层基函数节点和第j个输出节点的权重，权重值由奇异值分解(SVD)方法求解

具体为：设训练样本数量为N，式(7)可以用矩阵形式表示为Y=ΦS，其中Y是一个N×M阶的矩阵，Φ是一个N×(K+1)阶的矩阵，S是一个M×(K+1)的矩阵。则权值矩阵S是矩阵方程ΦS=D的最小二乘解，这里D是包含期望输出矢量N×M阶的目标矩阵。

2.3.2损失函数与参数迭代

采用误差平方和函数作为损失函数来评判EBFNN的拟合精度，则拟合目标矩阵D与EBFNN对应输出的损失函数为

(10)

为充分利用训练样本中输入输出关系对EBFNN中关键参数的影响，采用梯度下降训练算法获取损失函数与均值向量ck、全协方差矩阵Σk、偏差项Sj 0、权重Sjk的迭代关系。

2.3.3参数选择与模型结构

结合第1节中的离心喷头喷雾试验，EBFNN模型参数选择如下：输入层的样本数量为18，样本维数为2；隐层的神经元数量为18；输出层导出18组结果，样本维数为1；训练数据集合的数量为18，模型构建最大迭代次数为50。输入节点到隐层节点通过两个控制单元连接，分别是隐层基函数节点的均值向量ck和全协方差矩阵Σk；隐层节点到输出节点通过各隐层基函数的对应权重wjk控制。

3 离心喷头喷雾参数代理数学模型建立与分析

3.1 喷雾参数代理数学模型对比分析

将表1、2作为样本输入，分别基于四阶RSM模型、Kriging模型以及EBFNN模型构建粒径Dv50及其对应喷幅的代理数学模型。另外，评估代理数学模型误差精度的方法有：均值误差、最大误差、均方根误差、决定系数R2，4种方法的误差分别见表3、4。

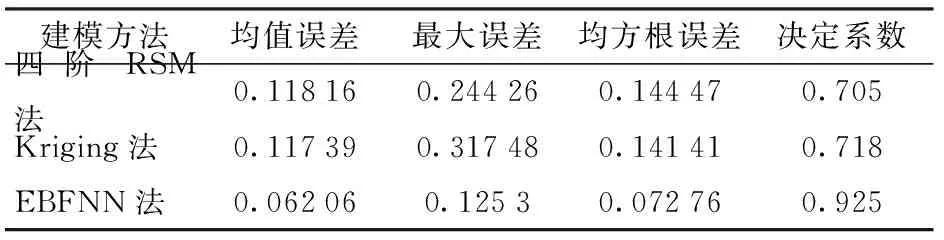
表3 3种代理模型对粒径的拟合精度对比Tab.3 Accuracy comparison of three agent models for particle size

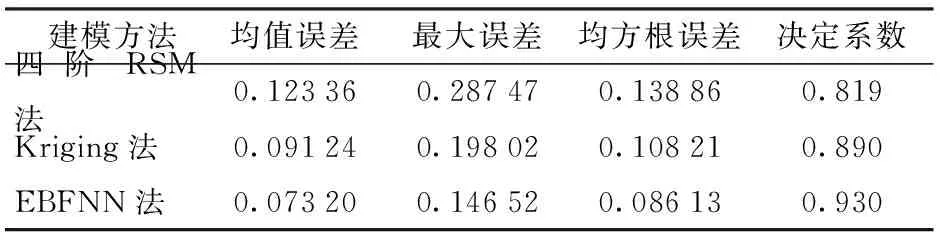
表4 3种代理模型对喷幅的拟合精度对比Tab.4 Accuracy comparison of three agent models for spray width

最后，用决定系数R2评估代理数学模型预测值与试验值之间的符合程度

(11)

式中Oi——输出试验值

O′i——隐式代理模型输出预测值

R2越接近1，表明隐式代理模型精度越高。选取18个样本点进行样本点分析。

结合表3及表4可以看出，3种代理数学模型中，Dv50及对应喷幅这两个响应的均值误差、最大误差、均方根差、决定系数差异较为明显，四阶RSM、Kriging法的3个误差参数较为接近，但EBFNN法的误差明显更小。总体来看，四阶RSM法的拟合精度最差，Kriging法稍好，EBFNN法的拟合精度明显最好。结果表明Dv50及对应喷幅两个响应目标92%以上的响应值均可以由EBFNN模型进行预测解释。

3.2 基于代理数学模型的喷雾参数分析

3种数学模型对Dv50的拟合误差精度如图6所示，从图中可以看出，四阶RSM、Kriging模型拟合精度较差，拟合点在中斜线两侧散布，而EBFNN模型对样本的拟合点较为集中地分布在中斜线两侧，综上结果可得出，EBFNN最适用于CN1215型离心雾化喷头Dv50的响应建模，可以进行粒径Dv50的分析、预测及智能决策。

图6 雾滴体积中径(Dv50)的代理数学模型Fig.6 Agent mathematical model of droplet volume diameter (Dv50)

图7 喷头流量及转速对雾滴雾化粒径的影响规律Fig.7 Effect of nozzle flow rate and rotation speed on particle size of droplet

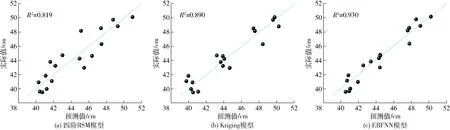
图8 对应喷幅(Dv50)的代理数学模型Fig.8 Agent mathematical model for corresponding spray amplitude (Dv50)

基于构建的CN1215型离心雾化喷头雾化粒径Dv50的EBFNN隐式代理数学模型，绘制出Dv50对试验因素离心泵流量、喷头转速的响应曲面，如图7所示。从纵向的视角来看，在泵的流量一定(全流量范围)的工况下，随着转速的逐渐增大，离心喷头的Dv50一直减小；从图7a也可以看出，泵的供给流量越小，在转速增大的过程中，离心喷头Dv50减小的速率更大；另外，在区间1(140～225 mL/min，8 000～8 400 r/min)、区间2(250～300 mL/min，8 000～8 200 r/min)内部，离心喷头Dv50处于高值域，明显大于其它区间。此外，从横向的视角来看，在喷头转速一定的情况下，随着泵的供给流量逐步增大，离心喷头粒径Dv50均呈现出先增大、后减小、再增大、再减小的趋势，在试验测量的范围内变化过程中，粒径Dv50会出现两个波峰；另外，从图7a可以看出，三维视图的响应面呈一定的螺旋状，对应图7b可以看出，在喷头转速较小的区域，粒径Dv50值的第1个波峰明显高于第2个波峰，且随着喷头转速的逐步提高，粒径Dv50值的第2个波峰逐步逼近第1个波峰、并逐步高于第1个波峰。

3种数学模型对雾滴体积中径Dv50对应喷幅的拟合误差精度如图8所示，从图中可以看出，从模型预测值和实际测量值的聚集度和决定系数R2来看，精度从高到低分别为EBFNN、Kriging、四阶RSM，EBFNN最适用于CN1215型离心喷头喷幅的响应建模，可以进行喷幅的分析、预测及决策。

基于构建的CN1215型离心喷头雾化粒径Dv50对应喷幅的EBFNN隐式代理数学模型，绘制出喷幅对试验因素离心泵流量、喷头转速的响应曲面，如图9所示。从横向来看，在喷头转速一定的情况下，随着泵的供给流量逐步增大，离心喷头喷幅均呈现出先减小、后增大、再减小、再增大且波峰呈阶梯状的上升趋势，对于测试范围内所有喷头转速，当泵的供液量为350 mL/min时喷头喷幅达到最大(除去喷头转速为9 900～10 000 r/min的区间，此区间喷幅达到最大值后又开始下降)。另外，从纵向的视角来看，在泵的流量一定(全流量范围)的工况下，随着喷头转速的逐步增加，离心喷头喷幅呈现出较弱的先增大后减小的趋势，当泵的供液量处在330～350 mL/min范围内，离心喷头喷幅增大到最大值后趋于稳定。

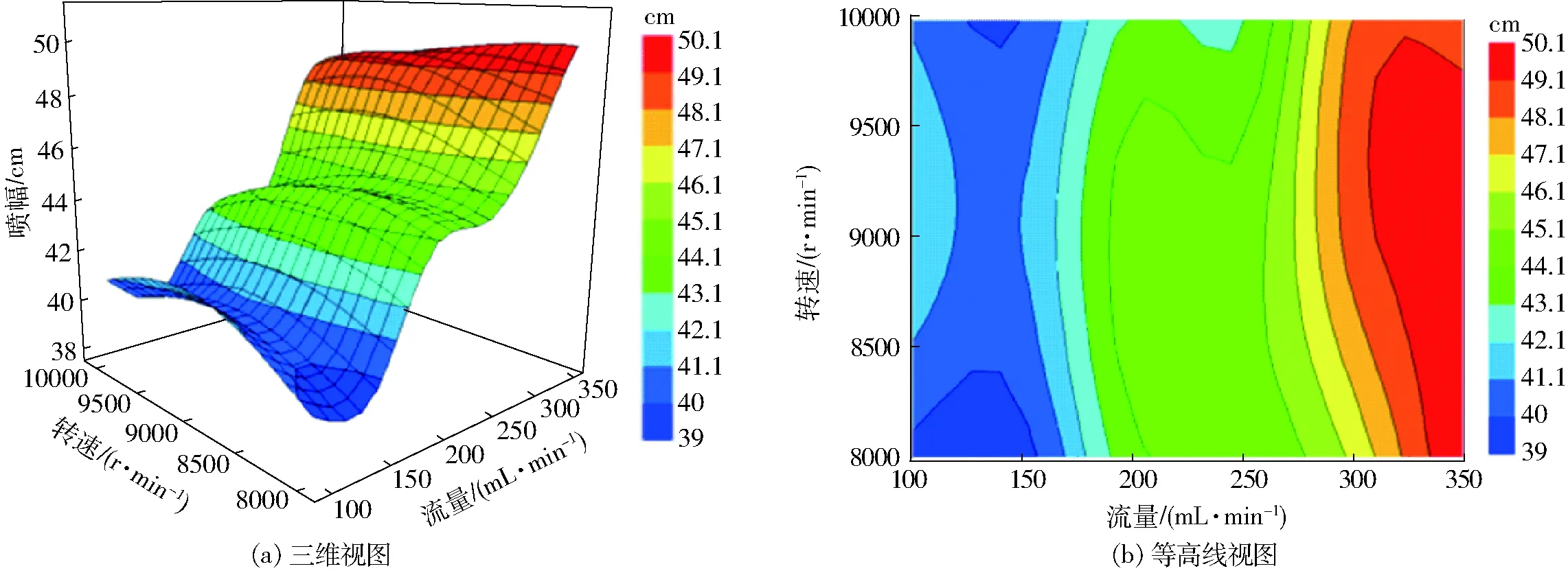
图9 喷头流量及转速对喷幅(Dv50对应值)的影响规律Fig.9 Effect of nozzle flow rate and rotation speed on spray amplitude (Dv50)

3.3 航空离心雾化喷头雾化性能参数预测

定义输入变量泵供液量为a(100～350 mL/min)、定义喷头的转速为b(8 000～10 000 r/min)，定义输出变量粒径Dv50为c1(μm)、定义对应喷幅为c2(cm)；基于粒径Dv50及喷幅的EBFNN模型，编写粒径Dv50及对应喷幅的预测界面，如图10所示。

图10 离心喷头雾化参数预测界面Fig.10 Centrifugal nozzle atomization parameter prediction interface

从图10可以看出，在测试范围内，输入任意组合的泵供液量a、离心喷头转速b，就能获得离心喷头雾化参数粒径Dv50及对应的喷幅。基于雾化参数的EBFNN模型，可以根据工作参数迅速预测雾化参数，这对变量施药系统的研发、施药飘移模型的建立提供了输入、响应参数的关系及建模初始边界(雾滴初始切向速度(由雾滴喷幅转化得到)、雾滴初始粒径Dv50)，为精准施药实施策略的制定提供了可靠支撑，如图11所示。

图11 离心喷头雾化参数预测策略Fig.11 Atomization parameters prediction strategy for centrifugal nozzle

4 结论

(1)针对CN1215型离心喷头喷雾参数(包括喷雾流量、喷头转速)，标定了供液系统的工作参数(包括离心泵的转速、喷头供电电压)，为不同工况下雾化参数的快速试验测试提供了支撑。

(2)搭建了离心喷头雾化粒径Dv50及对应喷幅的测试平台并按照试验方案展开了具体测试；分别采用四阶RSM、Kriging及EBFNN法建立了离心喷头Dv50及对应喷幅两个雾化参数表征因子与供液系统喷雾参数的响应关系的代理数学模型；对代理模型均值误差、最大误差、均方根误差、决定系数进行比较分析，结果表明，EBFNN拟合精度明显最优，适合CN1215型离心喷头雾化参数的数学建模。

(3)3种代理模型对Dv50的决定系数R2分别为：0.705、0.718、0.925，3种代理模型对Dv50对应喷幅的决定系数R2分别为：0.819、0.890、0.930。基于EBFNN模型，建立了响应曲面，分析了喷雾参数对雾化参数Dv50及对应喷幅的影响规律。当喷头转速一定时，随着供给流量逐步增大， Dv50均呈现出先增大、后减小、再增大、再减小的趋势；喷幅均呈现出先减小、后增大、再减小、再增大的阶梯状上升趋势。当泵的流量一定时，随着喷头转速的逐步增加， Dv50一直减小，而喷幅呈现出较弱的先增大后减小的趋势。