变速条件下农业机械路径跟踪稳定控制方法

段贤强 陶建峰 覃程锦 蔡道清 李彦明 刘成良

(上海交通大学机械与动力工程学院， 上海 200240)

0 引言

农业机械(简称农机)自动导航是精准农业技术体系的核心技术之一，广泛应用于耕作、播种、施肥、喷药、收获等农业生产过程[1]。近年来，控制技术、传感器技术、信息技术以及微处理器技术的高速发展极大地推动了农机装备智能化的进展，使得农业机械的自动导航控制技术受到了国内外学者广泛的关注[2-3]。

目前，农机自动导航跟踪控制方法主要有PID控制[4-6]、纯追踪模型[7-11]、智能控制[12-14]和模型预测控制[15-19]等。PID控制是一种对误差量进行线性组合反馈控制的方法，应用较为广泛。例如，文献[4]采用PID控制方法，在速度恒定时，农机直线跟踪精度较高，但在速度改变时，需要重新整定PID参数。基于纯追踪模型的控制方法是一种几何方法，其优点是无需对系统进行建模。文献[7]采用基于Kalman滤波和纯追踪模型的方法进行农机的自动导航，在固定前视距离和行驶速度的前提下，具有比较高的跟踪精度。然而，前视距离是影响控制精度与稳定性的主要参数，固定的前视距离的纯追踪模型控制方法对于农机速度变化非常敏感，在速度变化时，可能出现控制不稳定的情况。文献[11]采用模糊控制自适应调整前视距离参数，在两种不同速度下实现了农机的稳定控制。模糊控制方法不依赖于被控对象的物理模型。文献[12]建立模糊控制器对拖拉机转向进行控制，实现了对直线路径的跟踪。文献[13]采用基于遗传算法的自适应模糊控制方法，提高了系统的跟踪精度，但对于不同速度下的稳定性未进行研究。模型预测控制方法是基于农机的运动学或者动力学模型，预测农机未来一段时域的运动，根据评价函数，最优地选择控制量，其预测与控制效果依赖于数学模型的精度，即模型的精度与控制的实时性之间存在矛盾。文献[16]将非线性模型预测控制应用于拖拉机的自主导航，实现了泥泞田地中复杂路径的跟踪，但跟踪精度还有待提高。文献[20]提出了一种与行驶速度无关的农机路径跟踪方法，对农机的速度变化具有一定的鲁棒性，但在转向系统时间常数较大时可能存在振荡现象。

分析上述文献发现，当前农机路径跟踪控制在不同速度条件下仍存在稳定性和鲁棒性较差的问题。因此，为提高农机路径跟踪控制在不同速度条件下的稳定性和鲁棒性，本文提出基于链式系统模型和小范围稳定性分析优化的路径跟踪控制方法。以水稻穴直播机为实验平台进行直线路径跟踪对比实验和农机作业实验，以验证所提控制方法控制效果。

1 系统建模

1.1 农机运动学建模

自动导航控制车辆的物理模型一般为运动学模型和动力学模型。在低速时，车辆平台运动学约束影响较大，而随着速度的增加，动力学特性对运动规划与控制的影响就越明显[21]。由于农机一般为低速行驶，所以本文建立运动学模型。以待跟踪目标直线AB为X轴，垂直目标直线为Y轴建立田地XOY直角坐标系(图1)，以农机后轮轴线中点C为车身坐标点，根据运动学关系，建立运动学模型为

(1)

式中x、y——车身坐标点C横、纵坐标，m

θ——航向角，逆时针为正,(°)

δ——前轮转角，逆时针为正,(°)

v——车辆速度,m/s

l——车辆轴距,m

图1 田地坐标系Fig.1 Coordinate of field

1.2 前轮转向系统建模

农机前轮自动转向系统采用步进电机驱动，其电机转速与控制器输出成正比，故可以将前轮自动转向系统看作一阶惯性系统，为

(2)

式中δt——目标前轮转角,(°)

T——一阶惯性系统时间常数

转向曲率γ与前轮转角δ的关系为

(3)

当前轮转角δ较小时，则式(3)可以简化为

γ=δ/l

(4)

由式(2)与式(4)可得农机转向曲率速率为

(5)

式中γt——期望转向曲率

根据式(1)、(3)、(5)，可得前轮转角较小时农机运动学模型为

(6)

2 路径跟踪控制

2.1 转向控制方法

由式(1)可知，农机运动学模型是一个非线性模型，根据文献[22]所提的链式系统，将非线性的农机运动学模型转换为线性的链式系统，从而得到前轮转向控制方法。链式系统的一般表达式为

(7)

式中xn——状态量u1、u2——系数

为使链式系统为线性，将状态量对时间的导数用各个状态量对x1的导数替代，记为

(8)

则式(7)可改写为

(9)

农机运动学模型式(1)为三阶系统，链式系统和线性的链式系统的三阶式为

(10)

(11)

令x1=x，x2=y，根据式(1)和式(10)可得

(12)

(13)

由式(12)、(13)，可得

x3=tanθ

(14)

再根据式(8)和式(10)，可得u2和u3为

(15)

(16)

式(11)表示的链式系统为线性系统，将误差项进行线性组合，可得到控制律为

u3=-kyx2-kθx3

(17)

式中ky、kθ——位置偏差与航向偏差的比例系数

根据式(14)、(16)、(17)，可以得到期望前轮转角为

δt=arctan(lcos3θ(-kyy-kθtanθ))

(18)

2.2 小范围稳定性分析

在小范围速度条件下，将前轮转角为小角度的农机运动学模型式(6)在平衡位置y=0,θ=0处进行泰勒展开，保留一阶项，可得

(19)

式中φy、φθ、φγ——γt关于y、θ、γ在平衡位置y=0,θ=0处的导数

其中，农机行驶速度v由机器速度限制与工作要求确定。

由式(3)与式(18)可得

(20)

对式(20)分别求对y、θ、γ的导数,并代入平衡位置y=0,θ=0，可得

(21)

将式(21)代入式(19)，可得系数矩阵

(22)

由式(22)可得系统多项式为

(23)

式中I——单位矩阵

化简得

(24)

由Routh稳定判据得

(25)

式中a0、a1、a2、a3、A1——Routh判据系数

农机在平衡位置小范围稳定的条件为

(26)

2.3 转向控制优化

由稳定性条件式(26)知，当参数一定时，该方法在农机行驶速度小于固定值时才能够稳定，但在实际应用中，农机行驶速度是根据工作要求变化的，若采用上述方法，可能出现不满足该稳定性条件的情况，为提高农机在平衡位置小范围的稳定性，将线性链式系统转向控制律式(17)进行优化，优化后的控制方法为

(27)

(28)

式中v0——整定参数时的行驶速度

速度为v0时，稳定性条件式(26)成立，有

(29)

则优化后的期望前轮转角为

(30)

同样，按照Routh稳定判据可知，优化后农机在平衡位置小范围稳定的条件为

(31)

由式(31)稳定条件可知，在v≤v0时，由式(29)可得

(32)

则稳定性条件成立。

在v≥v0且v0≥1时，知稳定性条件

(33)

成立。

综上，优化后的控制方法满足小范围稳定性条件，农机在平衡位置小范围稳定条件与农机行驶速度无关。

2.4 系统仿真

为验证上述转向控制方法优化策略的有效性，在Matlab/Simulink仿真环境下，建立农机运动学与前轮转向系统模型，进行直线跟踪实验，对优化前后的农机控制方法进行仿真实验。

仿真初始条件设置如下：初始横向偏差为0.2 m，航向角偏差为0°，采样时间为100 ms，速度v=1.0 m/s，分别调整优化前后转向控制方法的参数ky、kθ，使得优化前后的转向控制方法在控制的快速性、稳定性和超调量等方面均表现良好。在速度v=0.5 m/s和v=1.5 m/s条件下，分别进行优化前和优化后控制方法的仿真实验，得到优化前后的转向控制方法的横向偏差与前进距离之间的关系。

在不同速度下，优化前控制方法的农机行驶路径横向偏差与前进距离之间的关系如图2所示，在速度v=0.5 m/s和v=1.0 m/s时，优化前控制方法具有收敛速度快、没有超调量和稳定等优点，但当速度增加至v=1.5 m/s时，优化前控制方法不再收敛。

图2 优化前不同速度下横向偏差Fig.2 Lateral deviation at different speeds before optimizing

优化后控制方法的仿真结果如图3所示，在不同行驶速度下，优化后的控制方法均能快速地收敛至平衡位置，并保持稳定。该仿真实验结果与理论分析结果一致，本文所提出的转向控制方法的优化方法能在速度增大时保持控制的稳定性。

图3 优化后不同速度下横向偏差Fig.3 Lateral deviation at different speeds after optimizing

3 实验与结果分析

3.1 实验平台

图4 实验平台Fig.4 Experiment platform

为验证所提出的控制方法，将洋马VP6E型水稻穴直播机(图4)进行自动化升级改造后作为实验平台，在原有结构基础上，增加自动转向系统、速度控制系统、高精度北斗定位系统、前轮转角测量传感器和车身姿态传感器等。

图5 不同速度横向偏差曲线Fig.5 Lateral deviation curves at different speeds

定位系统采用北斗高精度差分定位系统(RTK-GPS)，能以最高10 Hz的频率更新定位信息，其定位精度可达2 cm，航向精度可达0.1°。车身姿态传感器采用BW-VG525型动态倾角传感器，该传感器是一款高性能的惯性测量设备，其动态测量精度为0.1°，静态测量精度可达0.01°，最大输出频率为100 Hz，该传感器用于测量车身的横滚角与俯仰角，完成对车身定位数据的修正；前轮转角传感器采用MCGJ485B型绝对值角度传感器，测量精度为0.2°，主要对前轮转角数据进行测量。速度控制系统采用在现有油门结构基础上增加电动推杆-拉线的方式实现。通过以上自动化升级改造，搭建了基于ARM控制器的农机位置、航向、前轮转角信息的获取和方向盘与油门的自动控制导航平台。

3.2 实验结果与分析

采用上述的农机实验平台进行路径跟踪实验，验证所提出的控制方法。根据实验平台RTK-GPS实时采集的定位数据，得到期望路径与实际位置之间的误差，作为路径跟踪实验的跟踪误差。

3.2.1直线跟踪对比实验

实验平台在较为平整的水田中分别以3种不同速度(v=0.8 m/s、v=1.0 m/s和v=1.2 m/s)进行本文控制方法和PID控制方法直线路径跟踪对比实验，由于无需播种作业，则播种机具处于提升状态。根据PID控制方法可以得到期望前轮转角为

(34)

在速度v=1.0 m/s时，根据经验法，整定本文控制方法和PID控制方法,本文控制方法参数设定为ky=2，kθ=4，PID参数为kp=5,kd=1,ki=0.03，实验时为防止积分项绝对值过大，设定其最大为200，并且仅在其绝对值小于0.15 m时进行累加。实验时，通过高精度差分定位系统设定AB点，确定目标跟踪直线，农机行驶至目标直线附近，使得农机初始横向偏差为0.5 m，开启导航控制系统，农机沿着目标直线行驶至目标位置后关闭导航控制系统。分别采用本文控制方法和传统PID控制方法在上述3个速度下重复该实验。实验结果如表1所示。

表1 不同速度下横向偏差对比Tab.1 Comparison of lateral deviation at different speeds

在不同速度下的横向偏差与行驶距离的关系如图5所示。结果表明，在速度为0.8 m/s和1.0 m/s时，本文控制方法与PID控制方法均能保证控制结果收敛，且本文控制方法的横向偏差的平均绝对误差小于PID算法的平均绝对误差；在速度为1.2 m/s时，本文控制方法的控制结果收敛，平均绝对误差和最大绝对误差无明显增大，而PID控制不稳定。

3.2.2农机作业实验

农机在实际工作环境下不仅需要简单的点到点的直线跟踪，而且还需要按照规划路径遍历农田，根据水稻穴直播机按行播种的作业特点，采用梭行法遍历农田，得到农机作业规划路径,如图6所示。

图6 农机作业规划路径Fig.6 Agricultural machinery operation planning path

在作业时，设定农田的四顶点确定待作业农田，根据该实验平台的转弯半径，设置地头宽度，采用梭行法进行农机行驶路径的规划，农机行驶至目标路径起点，使播种机具处于下降状态，启动自动导航控制，农机自动完成目标路径的跟踪。农机作业跟踪路径如图7所示，实际作业路径如图8所示。

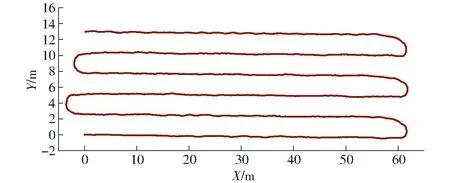
图7 农机作业路径Fig.7 Agricultural machinery operation path

图8 农机实际作业路径Fig.8 Agricultural machinery actual operation path

本文控制方法在各行的直线跟踪控制效果如表2所示，速度和横向偏差随时间变化关系如图9和图10所示。其中，横向偏差在每次换行转弯时发生突变；上线距离是指开始直线跟踪位置与农机横向偏差绝对值第1次小于6 cm时位置的距离；表2中实验数据均是上线后的统计结果。对比表1和表2可知，农机作业实验结果在平均绝对误差方面较直线跟踪实验结果增大较多，经过分析发现，主要有3个原因：

表2 各行直线跟踪结果Tab.2 Line tracking results

图9 速度变化曲线Fig.9 Velocity variation curve

图10 横向偏差变化曲线Fig.10 Lateral deviation variation curve

(1)直线跟踪对比实验和农机作业实验的初始误差不同。直线跟踪对比实验时，初始误差均为50 cm，而农机作业实验时，每次地头转弯初始误差均大于50 cm。

(2)直线跟踪对比实验和农机作业实验的实验环境不同。直线对比实验在水田中进行实验时，为保证本文控制方法与PID控制的实验环境条件相同，选择在较为平整的水田中重复多次实验；而田间作业实验则需要遍历整个田地。

(3)直线跟踪对比实验和田间作业实验时播种机具的状态不同。直线对比实验时，播种机具由于无需播种，则处于空闲状态，即提升状态；田间作业实验时播种机具处于工作状态，即下降状态，二者状态的不同导致机器负载变化也是影响作业精度的因素之一。

实验结果表明，在农机实际工作环境下，行驶速度0.4～2.0 m/s范围变化时，本文控制方法依然具有稳定性，平均绝对误差均值为0.047 m，最大绝对误差为0.128 m。进一步验证了本文控制方法对速度变化具有鲁棒性，并且具有较高的控制精度，适用于农机复杂的实际工作环境。

4 结论

(1)针对农机路径跟踪控制方法在不同速度下的稳定性问题，提出了一种基于链式系统模型和小范围稳定性分析的路径跟踪控制方法。通过理论分析和仿真实验，验证了其在不同速度条件下均能保持稳定性。

(2)采用水稻穴直播机在水田中开展了本文方法与PID控制方法的直线跟踪对比实验和农机作业实验。验证了本文控制方法在3种不同速度下稳定性优于常用的PID控制方法；农机行驶速度在0.4～2.0 m/s范围内变化时，本文方法能够保持稳定，平均绝对误差均值为0.047 m，最大绝对误差为0.128 m，适用于复杂的农机作业环境。