关于不定方程 x3+1=158y2*

李小丽，罗 明

(重庆师范大学 数学科学学院，重庆 401331)

0 引 言

关于不定方程x3±1=Dy2(D>0)已有不少研究工作，当D无6k+1形的素因数时，其全部解已由柯召、孙琦、曹珍富等[1]得到;当D有6k+1形的素因数时，方程的求解比较困难，目前方程x3+1=Dy20D>100还未被解决完。此处运用Pell方程、递归数列方法证明了当D=158时不定方程x3+1=Dy2仅有整数解(-1,0),(293,±399).

表1 X3+1=Dy2的整数解

引理1[2]不定方程4x4-3y2=1 仅有整数解(x,y)=(1,±1),(-1,±1).

引理2[2]不定方程x2-3y4=1 仅有整数解(x,y)=(±2,±1),(±7,±2),(±1,±0).

定理1 不定方程

x3+1=158y2

(1)

仅有整数解(-1,0),(293,±399).

证明因为(x+1,x2-x+1)=1或3，故不定方程式(1)给出了下列4种可能的分解：

情形Ⅰx+1=158a2，x2-x+1=b2，y=ab.

情形Ⅱx+1=2a2，x2-x+1=79b2，y=ab.

情形Ⅲx+1=474a2，x2-x+1=3b2，y=3ab.

情形Ⅳx+1=6a2，x2-x+1=237b2，y=3ab.

以下分别讨论这4种情形所给出的式(1)的整数解的情况.

情形Ⅰ解x2-x+1=b2得x=0,1，代入式x+1=158a2均不成立，所以该情形无不定方程(1)的解.

情形Ⅱ若2|a，则x+1≡0(mod 8)，即x≡-1(mod 8)，由x2-x+1=79b2有3≡7b2(mod 8)不可能，故2|a，所以x≡1(mod 8)，1≡7b2(mod 8)不可能.故该情形无不定方程式(1)的解.

情形Ⅲ由x+1=474a2和x2-x+1=3b2可得(2b)2-3(316a2-1)2=1.因为方程X2-3Y2=1的全部整数解由式(2)给出：

(2)

其中,316a2-1=yn.

当2|n时，2|yn与式(2)矛盾，故2| .

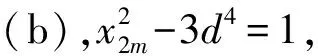
情形Ⅳ由x2-x+1=237b2,得237(2b)2-(2x-1)2=3，把x+1=6a2代入,得(12a2-3)2-237(2b)2=-3.

(3)

因此有12a2-3=xn=585un+9 006vn，也即是4a2=195un+3 002vn+1.

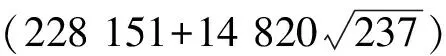
un+2=456 302un+1-un，u0=1,u1=228 151

(5)

vn+2=456 302vn+1-vn，v0=0,v1=14 820

(6)

zn=195un+3 002vn

(7)

zn+2=456 302zn+1-zn

(8)

(9)

un+2k≡-un(moduk)，un+2k≡un(modvk)

(10)

vn+2k≡-vn(moduk)，vn+2k≡vn(modvk)

(11)

zn+2k≡-zn(moduk)，zn+2k≡zn(modvk)

(12)

同理可证明：对递归数列取mod 23，其剩余类序列周期为8，当n=2(mod 8)时，4a2=Zn+1=21(mod 23)不成立，所以n=0,4,6(mod 8).

对递归数列取mod 97，其剩余类序列周期为8，当n=6(mod 8)时，4a2=Zn+1=83(mod 97)不成立.所以n=0,4,8,12(mod 16).

对递归数列取mod 17，其剩余类序列周期为16，当n=8,12(mod 16)时，4a2=Zn+1=10,11(mod 17)不成立，所以n=0,4(mod 16).

对递归数列取mod 113，其剩余类序列周期为16，当n=4(mod 16)时，4a2=Zn+1=74(mod 113)，不成立，所以n=0(mod16).

对递归数列取mod 67，其剩余类序列周期为22，当n=4,6,16(mod 22)时，4a2=Zn+1=43,66(mod 67)不成立，所以n=0,2,8,10,12,14,18,20(mod 22).

对递归数列取mod 109，其剩余类序列周期为22，当n=2,8,12,14,18,20(mod 22)时，4a2=Zn+1=96,14,53(mod 109)不成立，所以n=0,10(mod 22).

对递归数列取mod 397，其剩余类序列周期为22，当n=10(mod 22)时，4a2=Zn+1=203(mod 397)不成立，所以n=0(mod 22).

对递归数列取mod 73，其剩余类序列周期为12，当n=4,8(mod 12)时，4a2=Zn+1=43,56(mod 73)不成立，所以n=0(mod 12).

对递归数列取mod 103，其剩余类序列周期为13，当n=2,7,9,12(mod 13)，4a2=Zn+1=47,48,27,12(mod 103)不成立，所以n=0,1,3,4,5,6,8,10,11(mod 13).

对递归数列取mod 1 249，其剩余类序列周期为13，当n=1,5,8(mod 13)时，4a2=Zn+1=461,326,560(mod 1 249)不成立，故n=0,3,4,6,10,11(mod 13),即n=0,4,6,10,16,24(mod 26).

对递归数列取mod 22 699，其剩余类序列周期为26，当n=4(mod 26)，4a2=Zn+1=11 348(mod 22 699)不成立，故n=0,16,24,32,36(mod 52).

对递归数列取mod 112 100 717，其剩余类序列周期为52，当n=32,24(mod 52)时,4a2=zn+1=88 979 086,110 902 062(mod 112 100 717)不成立，所以n=0,16,36(mod 52).

对递归数列取mod 231 919，剩余类序列周期52，当n=16(mod 52)时，4a2=Zn+1=100 948(mod 231 919)不成立，所以n=0,36(mod 52).

对递归数列取mod 467，其剩余类序列周期为52，当n=36(mod 52)时，4a2=Zn+1=288(mod 467)不成立，所以n=0(mod 52).

递归数列取mod 31，其剩余类序列周期为10，当n=6,8(mod 10)时，4a2=Zn+1=30(mod 31)不成立，所以n=0,2,4(mod 10).

对递归数列取mod1 201，其剩余类序列周期为5，当n=4(mod 5)时，4a2=Zn+1=1007(mod1 201)不成立，所以n=0,2(mod 10).

对递归数列取mod1 147 921，剩余类序列周期10，当n=2(mod 10)，4a2=Zn+1=30 026(mod 1 147 921)不成立，所以n=0(mod 10).

所以n=0(mod 34 320).

如果n≠0，则可写n=2×2t×3×5×11×13×k，其中2|〗k，t≥3,对k分两种情况讨论:

1)当k≡1(mod4)，令

反复运用式(12)，可得zn≡z2m(modu2m)，再由

4a2≡z2m+1≡195u2m+3 002v2m+1(modu2m)，得：

表2 36um-3vm模190的结果

2)当k≡3(mod 4)，令

反复运用式(12)，可得zn≡-z2m(modu2m),再由4a2≡z2m+1≡-195u2m-3 002v2m+1(modu2m)

同式(13)计算得到：

根据m的取值对{38um+3vm}取mod 3,7,11，有

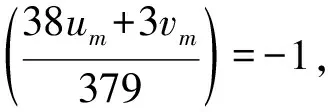
当n=0时，有4a2=z0+1=196，得a=7，由x+1=6a2，x2-x+1=237b2，y=3ab，得到式(1)的另一组解(x,y)=(293,±399).

综合几种情形的讨论结果，知式(1)仅有整数解(-1,0),(293,±399).

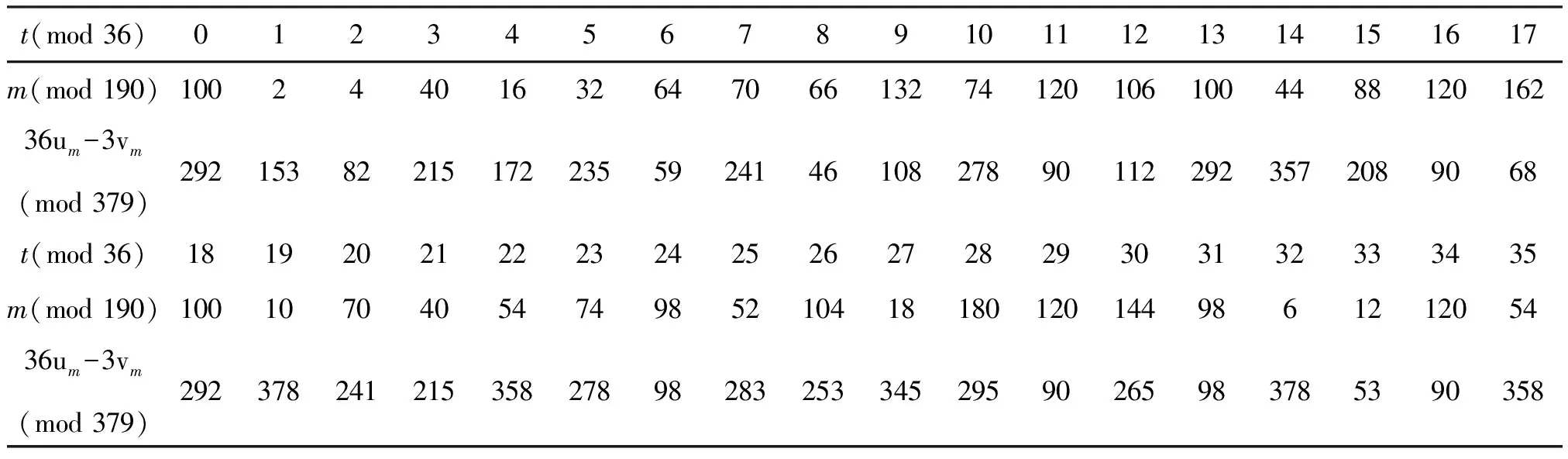
表3 36um-3vm模190的结果