组合核支持向量机个人信用评估模型*

张 玥，赵 凯，黄全生

(安徽工程大学 数理学院，安徽 芜湖，241000)

0 引 言

为了扩大国内市场需求，银行信用贷款、蚂蚁花呗等个人信用借贷平台如雨后春笋般不断推出，个人信用消费行为日趋增多，个人信用评估也开始受到政府和企业的重视。个人信用评估方法研究的重要性被人们发现,对降低商业银行的信用风险损失以及提高银行的工作效率、刺激普通消费者对信用贷款申请的积极性、推动我国经济的增长有非常重要的现实意义。

传统信用评估模型一般可以分为3类：专家评分模型[1]、统计模型[2]和人工智能模型[3]。数据的爆炸式增长、广泛可用和巨大数量使得真正的大数据时代到来。对于这些数据,人们不仅希望能够从中提取出有价值的信息,更需要发现对决策有效支持的更深层次的规律。因此,随着观念的转变,人们也把目光从传统数据挖掘转向机器学习。支持向量机(SVM)的概念在1963年被提出，在人脸识别、文本分类、手写识别和生物信息等方面得到广泛的应用[4-7]。其中核方法是近年来行业研究的重点。

在本研究中，使用向量机中的直方图交叉核、热核特征核、杰卡德距离核和余弦广义距离核[8-11]对个人信用数据的离散类型和连续类型进行并行处理，在此基础上，在预判环节对核函数进行了整合，其中权重由各个核函数对训练样本的分类精度决定。使用了德国商业银行信用卡业务客户的个人信息中的数据来测试模型，并与其他数据挖掘和机器学习的方法进行了比较。

1 核支持向量机个人信用评估模型

1.1 核支持向量机

支持向量机是一种基于核的学习方法，不同的核函数对支持向量机的性能有着不同的影响[12]。随着核函数在模式识别领域的理论和实践上发生的革命性的变化，特别是在图像分类方面，核函数在解决分类问题上起的重要作用被人们所认可。实际上，由几种常见线性的或非线性的基础模型拓展出的核函数，在核支持向量机分类模型中有着大量的应用。

如何获得一种有效的核函数选择方法成为核支持向量机研究领域的一个重要课题。由于不同的核函数具有不同的几何测量特性，选择合适的核函数可以满足支持向量机的泛化能力。然而，传统的核支持向量机核函数存在很大的局限性和盲目性。

国内外有很多学者通过实例考证这一情况[13]。如王晓慧、李云飞[14]将支持向量机方法与判别分析法、C5.0法和KNN法进行分析比较,发现支持向量机个人信用风险评估模型具有比较高的评估精度；肖文兵等[15]对支持向量机个人信用评估模型以及最优参数的选取进行了分析研究,并将基于支持向量机的模型与其他分类方法比较分类识别效果,结果显示在合理设置参数的情况下,支持向量机具有更好的预测效果。

现设采用n个指标参与评估,已有样本m个(X1,…,Xm),Xi=(xi1,…,xin),评价值yi,i=1,2，…,m,yi只取-1或1,1代表不违约,-1代表违约。

如表1所示，列举了几种不同性能的核函数。在实际支持向量机解决问题时,核函数的形式以及其参数决定了分类的复杂程度,它体现了支持向量分类器的性能。如何选择相关核函数取决于分类任务自身的数据分布, 对问题要有一定的先验知识;否则, 只能凭借经验或者凑试法, 来选择误差最小的核函数。

1.2 整合核方法

在个人信用评估模型中，客户的个人信用数据有很多种属性，这些属性有离散类型的，比如年龄、性别等；也有连续类型的，比如收入、存款等。在面临这种包含不同数据类型的样本时，在核函数的选择方面进行了特殊的处理：根据处理不同类型数据的核函数能力不同，让不同的核函数分别对离散类型数据和连续类型数据进行并行处理。从前人的研究成果中发现，直方图交叉核与热核特征核更适合处理离散数据，余弦广义距离核和杰卡德距离核更适合处理连续数据。处理过程如图1所示。

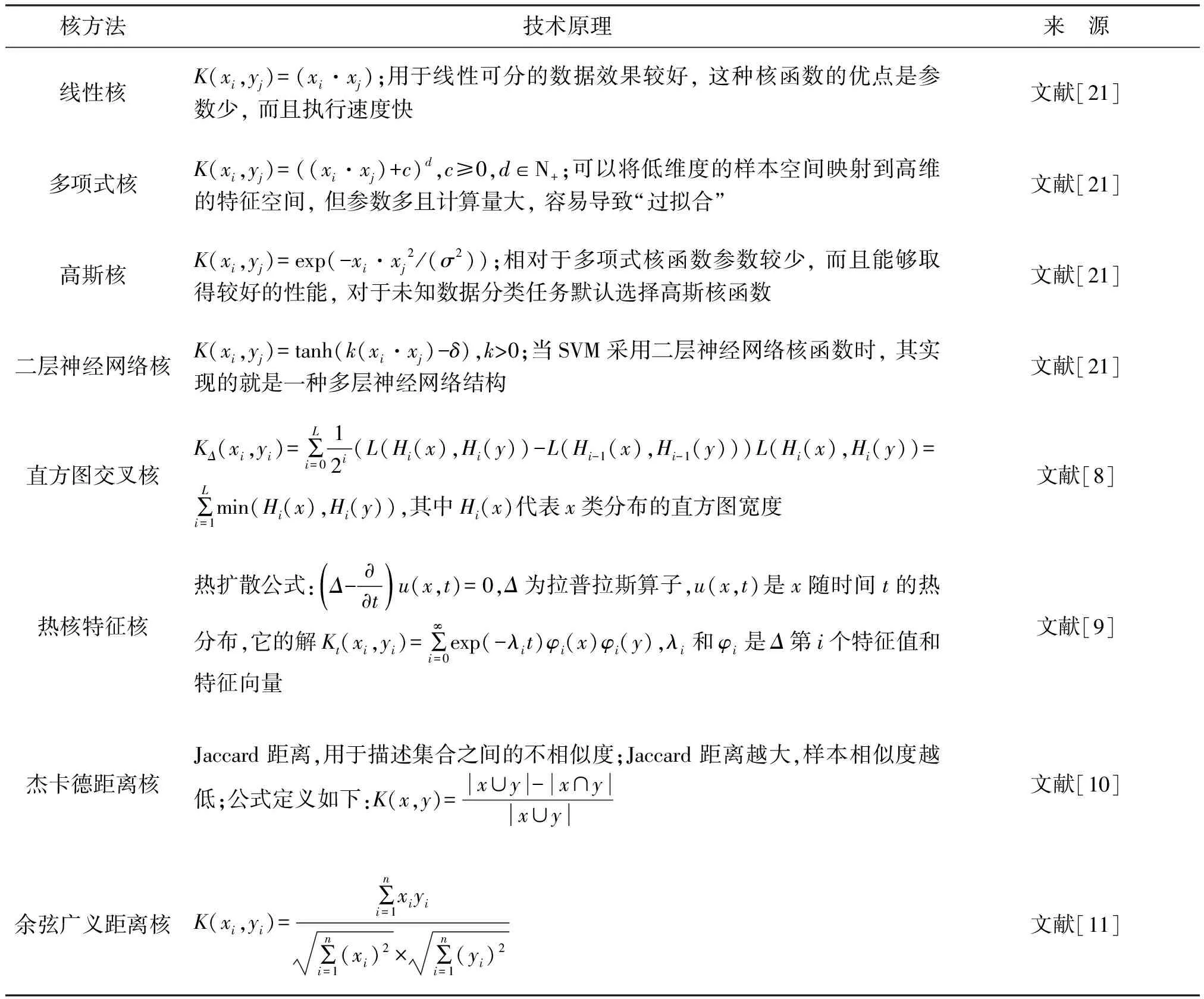
表1 核方法

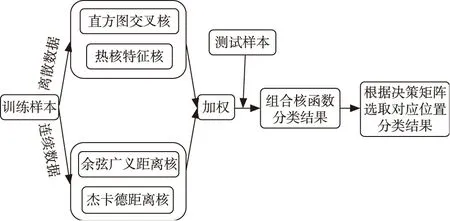
图1 模型流程图

首先用4个核支持向量机对训练样本进行分类，分类准确度分别为w1、w2、w3、w4，那么权重W为

接着定义表决矩阵V：

其中n代表核支持向量机的个数，m代表测试样本数。v(i)是单位矩阵的第i行，i的秩由类的数量决定。例如，对于个人信用评估“好”、“坏”两类系统，b(i.j)是1，2中的元素，有2×2的单位矩阵。b(i.j)的元素构成了V。最终决策方程Dj是加权向量W和表决矩阵V的点积：

2 实 验

2.1 数据预处理

数据来源于德国商业银行的客户信息共15万条客户记录，每条记录有9个属性项，对其进行分类处理，如表2所示。

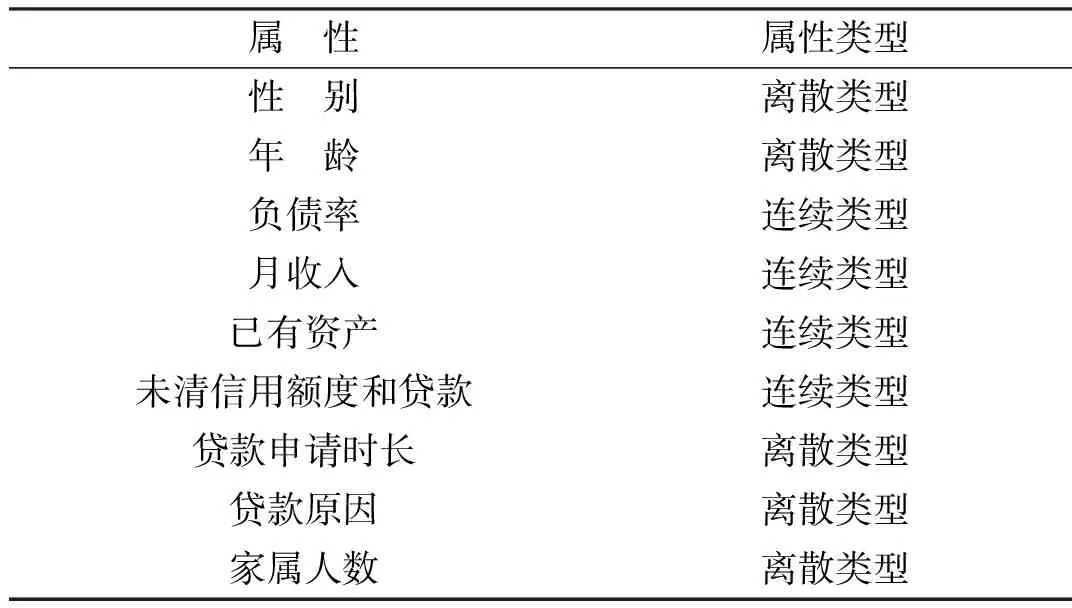
表2 数据类型的预处理

2.2 实验结果

实验是在Matlab2016a上实现的，参数配置如图2所示：

图2 实验配置

2.2.1 寻找最优参数

但是在实际应用中，却面临着几个重要的超参数的调优问题。如果调得不好，会影响分类效果。所以首先对需要选择参数的直方图交叉核与热核特征核进行参数选择。

从图3、图4和图5中可以看出:对于直方图交叉核的两个参数在(0.4,0.4)的时候效果最好，而热核特征核的参数在(1.4)的时候效果最好。所以选取它们作为核参数。

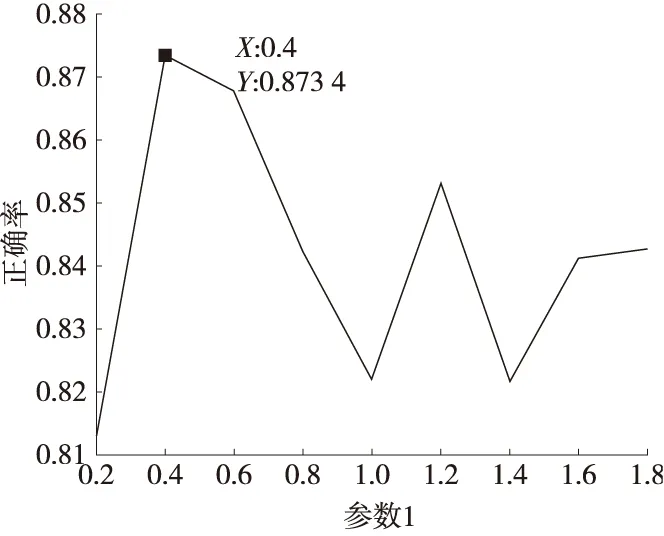
图3 直方图交叉核参数与正确率

图4 直方图交叉参数与正确率

图5 热核特征参数与正确率

2.2.2 4种核方法与整合核方法抽样实验

如图6所示，采用随机抽样的方法，分别抽取10次，每次递增总样本的10%作为训练样本。用4种核方法以及整合后的方法对其进行了实验。从图中可以看出整合后的核方法在对客户信用信息数据集上的实验中获得了比单一核方法更高的预测准确率。随着测试样本取样数量的递增，整合核方法预测准确率也比较稳定，能够保持较高的准确度，并且它的准确度相较于其他3种算法随折变化的波动相对平稳。

图6 加权前4种核方法与加权后整合方法分类正确率结果对比

2.2.3 5种数据挖掘与机器学习方法交叉验证

表3所示是采用5次交叉验证的方法对5种方法的预测准确率的实验结果。在表1中可以通过数字发现，支持向量机整合核方法5次交叉验证的预测准确率均值最高，高达93.72%，支持向量机方法的平均准确率次之，而贝叶斯分类方法、决策树方法和关联规则方法的平均准确度比较低，其中关联规则方法的平均准确度才67.32%；并且支持向量机整合核方法的标准差也是这5种算法中最小的，贝叶斯分类方法和关联规则方法的标准差甚至高达10.81%和12.89%。从这些数据中不难发现，对核函数进行了整合的支持向量机整合核方法不管是准确率还是稳定性都会有明显的提升。其中支持向量机整合核方法不但是分类效果最好的，而且是稳定性最高的。这说明，所提整合方法起到了显著的效果。

表3 交叉验证结果

从实验中可以得出，组合核支持向量机模型确实可以提升算法的分类正确率。在对离散数据和连续数据的处理上，对比不同核函数的分类性能找到了合适的核函数。相比于传统的支持向量机核函数的选择，选择的核函数具有稳定、高效、全面的特点，而且，核函数的加权方法也至关重要。所以说，在支持向量机模型中，核函数的应用是否合适，也是影响个人信用评估准确率的重要因素。

3 结束语

提出了一种新的基于支持向量机的个人信用评估模型，通过对支持向量机直方图交叉核、热核特征核、杰卡德距离核和余弦广义距离核的组合处理，对原始个人信用评估数据中的离散数据和连续数据分别处理，找到最适合的参数，挑选合适的核方法来达到分类精度的提升。并且构造了投票矩阵，根据每种核函数对训练样本的分类准确度对每种核函数进行了科学的加权。在实际应用中，模型具有科学性、先进性，并且拥有良好的适应性，可以获得满意的分类结果。通过实际数据实验，获得了良好的分类结果，同时证明了支持向量机自适应组合核加权模型在信用评分系统中具有良好的性能。因此，基于支持向量机的个人信用评估模型确实可以帮助银行或贷款人做出正确的决策。当然，模型还有着广阔的提升空间，学习更先进的理论知识来完成对模型的升级，是接下来需要努力的方向。