基于小波变换的双端输电线路行波故障定位*
孔垂祥, 杨 岸, 祝龙记
(安徽理工大学 电气与信息工程学院,安徽 淮南 232001)
0 引 言
高压输电线路作为电力系统的重要组成部分之一,担负着传输电能的重要职能。高压输电线路发生故障后,迅速准确地进行故障定位,既可以减轻寻线负担,又可以缩短供电恢复时间,减少因停电造成的经济损失,对电力系统运行的可靠性和经济性具有重大意义[1]。
现有的故障定位方法主要有故障分析法[2]和行波法。故障分析法是一种通过检测电气量求解电压平衡方程的定位方法,在原理上可以消除过渡电阻的影响,但在数据同步以及线路不均匀换位方面容易造成定位出现误差。行波法定位精度高且计算原理简单,不受线路参数、故障电阻和故障类型的影响,但在检测故障行波到达检测点时间和行波波速不确定性方面容易造成定位精度降低[3-7]。张媛媛等[8]提出一种利用双端正序电气量故障定位方法,改善了传统方法计算复杂的弊端,但没有考虑两端非同步角对定位造成的误差;胡斌等[9]提出一种基于行波固有频率和VMD(变分模态分解)的定位方法,具有良好的模态稳定性,但其定位精度受线路参数和行波反射信号衰减影响较大;周会峰[10]利用故障初始行波、反射波和对端母线反射波到达各测量点时间消除波速对定位的影响,但当反射波衰减至无法测量时会导致定位失败。
综上所述,为了消除过渡电阻、行波波速和线路参数等因素对故障定位精度的影响,本文提出一种基于小波变换的双端输电线路行波故障定位方法。该方法先将采集到的故障电流行波信号进行相模变换,再对得到的线模分量进行小波变换,得到行波波头首次到达各测量点的时刻,然后进行故障定位,最后通过MATLAB仿真验证了该方法的准确性和有效性。
1 电流行波信号分析
高压输电线路发生故障的同时,会产生向线路两端传播的故障暂态电流行波,准确快速地检测出行波波头是行波定位法的关键。小波变换具有较好的时域和频域局部化性能,这一特点使其在非平稳领域解析具有明显优势,因此小波变换成为检测行波信号波头的有效工具[11]。
1.1 基于小波变换的电流行波信号波头检测
设任意函数f(t)是一个平方可积函数,记作f(t)∈L2(R),φ(t)是一个基小波函数,将函数f(t)在基小波函数下进行展开,则函数f(t)的小波变换为
(1)
式(1)中,a>0,a为伸缩尺度因子;τ∈R,τ为位移尺度因子。
检测点采集到的电流行波信号是一种具有突变性质的非平稳信号,突变点标志着电流行波信号到达检测点。小波变换的模极大值与电流行波信号突变点是一一对应的且模极大值对应电流行波信号到达检测点的时刻。本文采用MATLAB中的db-4基小波对电流行波信号进行小波变换,识别电流行波信号波头到达检测点的时刻。小波变换的模极大值定义如下:
设f(x)为原始信号,在x0的某一领域,对一切x∈(x-δ,x+δ),有:
(2)

1.2 电流行波信号模量的选取
当三相输电线路发生故障时,各相之间存在的电磁耦合作用会影响故障定位的精确性。为了将三相不独立的行波分量转换为相互独立的行波分量,文中采用Karrenbaur变换对行波分量进行解耦。Karrenbaur变换矩阵为
(3)
式(3)中,i0、iα、iβ分别是电流0模分量、α模分量、β模分量,ia、ib、ic分别是三相线路的A相、B相、C相相电流。其中0模分量受零序电阻和零序电感影响比较大,β模分量在电流行波信号传播过程中衰减较大,故本文选取α模分量进行故障定位。
2 双端输电线路故障定位方法
双端输电线路如图1所示,M、N分别为两侧电源端的检测点,MN距离为L。P为M、N两端之间的一个检测点,到M、N两端的距离分别为L1、L2。故障电流行波波头首次到达M、N、P端的时间分别为tM、tN、tP,故障点与测量点P的距离设为x。行波波速在同一输电线路中是恒定不变的,故设行波波速为v。为保证各端同步采集信号,需配备高精度的GPS同步时钟和无线通信GPRS[12-13]。

图1 双端输电线路示意图
假设故障点发生PN端,此时tM>tN,由图1可列方程:
(4)
(5)
对式(5)解方程可得:
(6)
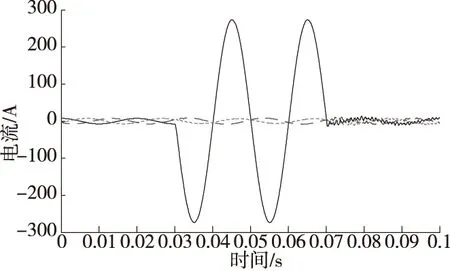
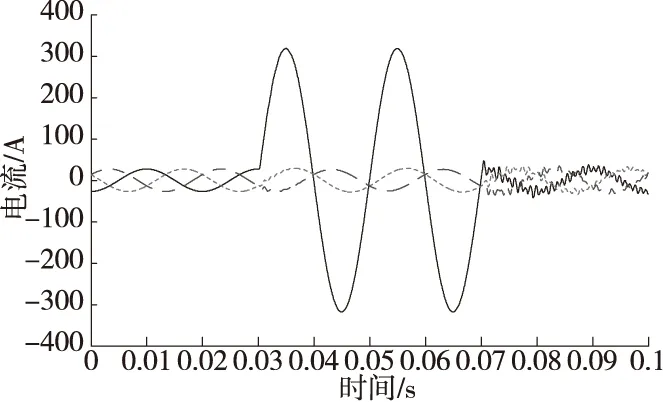
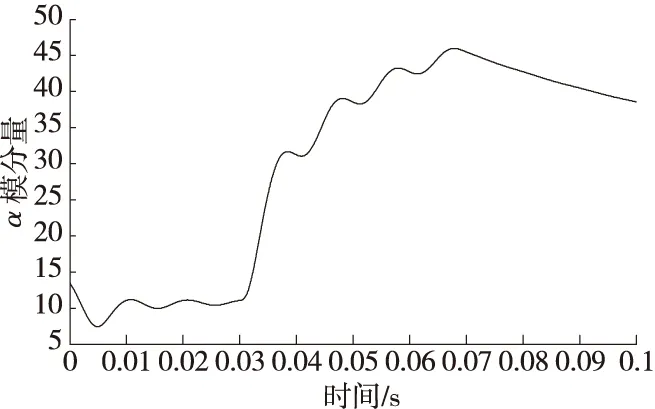
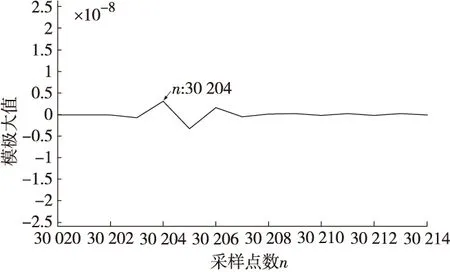
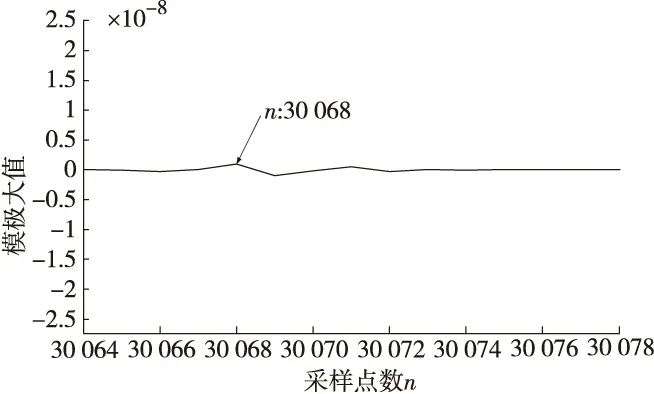
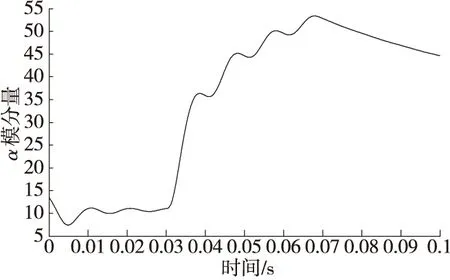
同理,当故障发生在MP之间时,此时tM (7) 当故障发生在P点时,此时tM=tN,此时x=0。 可见,该方法只需要检测出电流行波波头到达各测量点的时刻即可实现故障定位,与电流行波波速无关。双端输电线路故障定位流程如图2所示。 图2 故障定位流程图 为检验所提方法的正确性,以在PN两个检测点之间发生A相接地故障为例,在MATLAB中搭建如图1所示的输电线路仿真模型。仿真参数设置如下:仿真时长0.1 s,故障发生时间为0.03~0.07 s,采样频率为1 MHz,L1全长40 km,L2全长70 km,MN两端三相电源电压等级为220 kV,过渡电阻为300 Ω,输电线路参数如表1所示。 表1 输电线路参数 当故障距离P端为20 km时,在M、P、N端检测到的电流信号分别如图3中的(a)(b)(c)所示。 (a)A相短路时M端电流信号 (b)A相短路时P端电流信号 (c)A相短路时N端电流信号 图4 测量点M的α模电流行波分量和小波变换结果 图5 测量点P的α模电流行波分量和小波变换结果 图6 测量点N的α模电流行波分量和小波变换结果 由图4—图6可知,故障初始行波到达各测量点时间tM=0.030 204 s,tP=0.030 068 s,tN=0.301 70 s。代入式(6)计算后,故障与P测量点的距离x=20 km,测距误差为0。 继续对不同故障类型、过渡电阻和故障距离进行了仿真验证,仿真结果如表2—表4所示。 表2 故障距离20 km不同故障类型下的定位结果 表3 故障距离20 km不同过渡电阻下的定位结果 表4 MP段发生故障时不同故障距离情况下的故障定位结果 表2—表4充分表明,该方法不受故障类型、过渡电阻和故障距离的影响,具有良好的适用性,测距误差在1%之内,可以高精度地实现故障定位。 提出了一种基于小波变换的双端输电线路行波故障定位方法,与传统方法相比,该方法消除了行波波速和线路弧垂对故障测距的影响,通过对α模电流行波信号进行小波变换检测初始行波到达各测量点的时间,大大提高了定位精度。大量的仿真结果表明,该方法在不同故障情况下都具有良好的适用性,满足电力系统中故障定位的要求。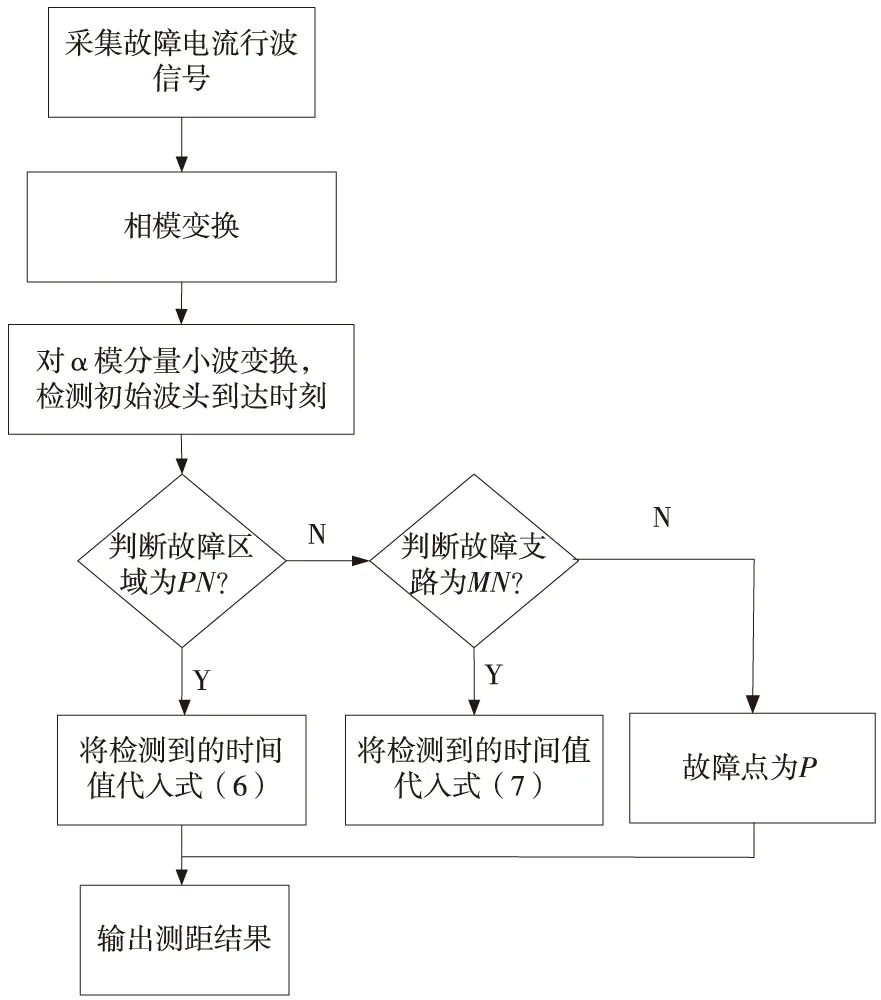
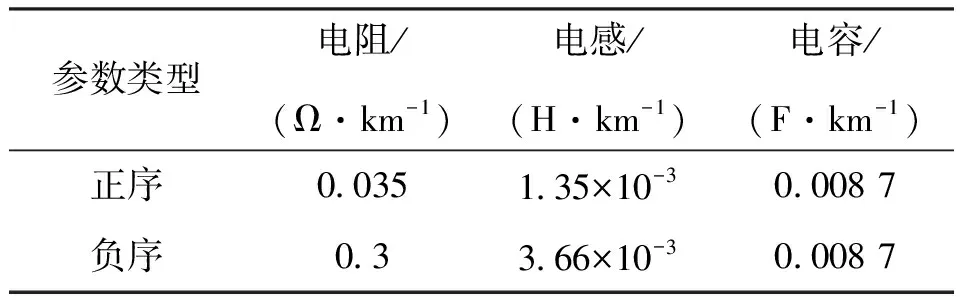
3 仿真分析






4 结 论

