椭圆轨道卫星对地全球覆盖电推进控制
马 雪,刘羽白,雷拥军,田科丰,陆栋宁,辛优美
(1. 北京控制工程研究所,北京 100094;2. 空间智能控制技术重点实验室,北京 100094)
0 引 言
大部分环绕中心天体的航天器轨道都是偏心率近似等于零的圆轨道,航天器在一个轨道周期内轨道高度相等,以匀角速度运行。然而,一些航天任务需要将卫星运行至偏心率不为零的椭圆轨道上,以满足某些特定的对地需求。例如美国的KH系列卫星,运行在近地点260 km、远地点1000 km左右的太阳同步轨道上,主要功能为在近地点进行更高分辨率的成像。KH系列卫星的拱线经过妥善设计,例如KH-12,在标称轨道上111天内可以通过自然摄动实现近地点星下点的全球覆盖(如图1所示)。不仅如此,还携带5~7 t燃料,用以调整拱线和轨道高度,实现任意区域的近地点详查[1-2]。又例如俄罗斯的闪电轨道通信卫星,运行在远地点40000 km的12 h轨道上,主要功能为在远地点为高纬度地区进行通信覆盖[3]。此外,深空探测器由于受到捕获能量的限制或具有多目标任务的特点,往往也采用大椭圆轨道。例如水星探测器MESSAGE[4]、木星探测器JUNO[5-6]等。深空探测器上的科学载荷最佳工作区域同样位于近地点附近。事实上,在行星科学领域,科学家对行星不同纬度上的地貌和成分差异关注度较大。然而仅依靠微弱的轨道摄动作用,在航天器有限的任务期间内大多难以实现近地点对整个纬度的遍历。这就导致单一航天任务无法实现对目标天体的全球范围详查,影响深空任务的完成质量。
综上所述,椭圆轨道卫星星上载荷的工作弧段多位于近/远地点附近,因此在对地任务上不具有连续性。而针对拱线星下点覆盖的轨道设计和拱线指向控制,目前已有实际的星上应用实例,并在日益复杂的航天任务下,具有较为强烈的需求。
然而,目前利用传统的化学推进系统实现对椭圆轨道卫星拱线星下点对地变换与覆盖的人工控制的燃料消耗较大,进行轨道控制的任务次数也较为有限。所幸,随着大功率太阳能/核电推进系统的日益成熟,具有高比冲的电推力器可以采取连续小推力的控制方式,使对椭圆轨道拱线对地覆盖性能的控制更具可行性和实用性。

图1 KH-12卫星近地点星下点全球覆盖情况Fig.1 Global coverage of subastral points of KH-12’s perigee
近年来,小推力轨道控制被应用于各类轨道控制问题,例如小推力轨道闭环制导控制[7]、太阳同步轨道机动控制[8]、人工太阳同步轨道[9]、轨道相位调整等[10]、多圈小推力轨道转移[11]等。而对于卫星对地特性的轨道设计与轨道控制,也有少量的文献进行研究。文献[12-13]研究了在J2项摄动下近圆轨道的星下点机动控制问题,给出了不同形式的脉冲推力下的解析解。文献[14]给出了利用电推进实现星下点机动的控制算法。文献[15]研究了利用化学推进或电推进实现星下点机动的优化策略。文献[16]研究了回归轨道的形成条件,并给出了多脉冲下的回归轨道控制与保持策略。文献[17]利用了迭代修正方法确保了轨道设计的星下点回归性。文献[18]研究了利用连续小推力控制策略形成任意轨道要素的冻结轨道。这些研究的主要目标是实现近圆低轨道上卫星对星下点目标的接近和转移问题。而对椭圆轨道覆盖特性和拱线对地指向的控制的研究开展的较为欠缺。
为此,本文以实现椭圆轨道卫星全球覆盖的人工控制为研究目标,综合考虑了椭圆轨道卫星运行的安全性,提出了一种连续小推力下的解析控制策略,并对该策略下的燃料消耗进行了一定程度的优化。
1 自然摄动对椭圆轨道全球覆盖的影响
当卫星的运行轨道受到各种摄动的影响,轨道根数会发生缓慢变化,这势必会影响卫星对地的星下点特性,同时叠加地球自转,二者引起星下点在地面上规则运动。特别是近地点高度极低的椭圆轨道,主要受到地球非球形摄动,特别是主导项为J2项带谐项的影响。
由于地球非球形摄动属于保守力,因此长期来看轨道半长轴保持不变,但对某些特定的轨道根数存在长期影响。通过轨道分析理论,对J2项摄动对应的势函数在一个轨道周期内进行平均化,以消除与轨道平近点角相关的短周期项,可得
(1)
式中:J2为二阶带谐项常数,μ为引力常数,Re为地球半径,a为轨道半长轴,e为轨道偏心率,i为轨道倾角。由式(1),进一步推导出由J2项非球形摄动引起的平均化轨道摄动方程:
(2)
(3)
(4)
(5)
(6)

(7)
式中:ns=0.9856(°)/d为地球公转角速率。又由式(5)、式(6)相除,可知当轨道倾角确定时,升交点赤经和近地点幅角的变化规律之间的比值是一定的:
(8)
这就意味着当自然摄动存在的情况下,太阳同步轨道卫星的近地点幅角进动角速率是不可设计的。
对于椭圆轨道卫星,其近地点的星下点经纬度可列写为:
(9)
δp=arcsin(sinωsini)
(10)
远地点星下点经纬度可列写为:
λa=arctan(tan(ω+π)cosi)-G0+
(11)
δa=arcsin(sin(ω+π)sini)
(12)
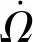

而对于轨道高度更高的高纬度通信卫星或深空探测器,也会受到多体引力摄动的影响。在基于中心天体与第三体摄动平面内的坐标系下,经过两次平均化可得到近地点幅角的变化率可表示为
(13)
式中:μs为第三体引力常数,as为第三体半长轴,es为第三体偏心率。该类摄动对拱线变换的影响通常更为缓慢。
而对于其他复杂的轨道摄动,或是未知中心天体的特性,也可通过轨道测量,以数值的形式表现,同样可以用作第2节中对拱线控制的自然摄动补偿项中。
综上所述,若对卫星远/近地点星下点的对地覆盖特性加以人工控制,其核心在于对轨道拱线,即仅对近地点幅角的变化率的控制。但在实际的控制策略的设计上,却面临很多待解决的问题和约束:
1)利用具有连续小推力特性的电推进进行轨道控制是一种节省燃料的高效控制方式,但以往的对轨道控制方式多解决的是化学推进基础上的脉冲控制,因此必须设计出一种连续小推力的近地点幅角控制策略。
2)椭圆轨道的近地点高度往往极低,在进行小推力控制时,必须防止卫星与地面相撞。同时,对于地观测卫星,近地点高度也不宜过高,以保证对地拍照的分辨率指标。因此,在进行小推力控制时必须维持相对稳定的近地点高度。
3)为节省燃料消耗,在控制律的设计上,需要考虑推力大小和方向的最优性问题。
4)由于星载计算机的计算能力有限,若需要提高自主性,需要将算法简化到能够在星上实现的程度。
2 小推力星下点全球覆盖控制
2.1 全球覆盖控制策略
在本文中,假设推力为连续控制形式,矢量和大小是可调节的。在第1节中,可以得到改变卫星近/远地点的星下点对地覆盖速率,同时受到星下点纬度和经度变化速率的共同影响。近/远地点星下点经度可受中心天体自转影响,无需控制即可实现全球遍历;近/远地点星下点纬度自然变化较慢,需要对卫星近地点幅角的变化率进行调整。因此,对近/远地点星下点覆盖速度进行控制,仅需在轨道面内施加控制力。
燃料消耗极小所对应的目标函数,与推力器的安装方式、是否采取矢量调节机构等技术细节有很强的相关性。本文设置每一轨道周期进行的目标函数为
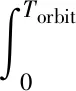
(14)
类似于推力器分别安装在径向和横向的推力指向的平方。该函数在较大程度上指征燃耗次低的情况,且形式简单更有利于得到解析解。若需要进行星上低计算量计算,更倾向于选用该种形式。对于具体推力配置,可选取相应的其他目标函数,但选取何种目标函数,均可用本文的方法进行全球覆盖小推力控制,在计算流程上没有本质区别。

(15)

(16)
其中,E(t)为卫星偏近点角。本文在式(16)中引入偏近点角E,是由于含偏近点角的轨道控制方程形式更加简洁和便于计算。
本文提出的控制方式,解决的就是满足近地点幅角变化率约束Δωtarget(式(15))的,令轨道面内控制力S(t)、T(t)在一个轨道周期内最小(式(14))的控制策略。

(17)
考虑到实际工程约束,电推力器可能由于遇到阴影,或进行其他在轨操作,有可能无法在整轨均处于连续开机状态。为安全起见,将对近地点半径不变的约束必须当成瞬时值来处理。因此,令式(17)等于0,将径向控制量S(t)向控制量T(t)表示:
S(t)=
(18)
观察式(18),S(t)的分母存在sinE项,意味着当偏近点角E=0时所需的径向控制力S(t)为正无穷,这在物理上是不可能实现的。因此需要避免奇异,使控制量变得合理可行。将横向控制加速度T(t)内加入sinE乘子,表示为:
T(t)=sinE(t)N(t)
(19)
其中,N(t)为待优化的控制函数。由此,代入式(18),可得径向控制加速度为:
S(t)=
T(t)=
(20)
此时,径向控制加速度分母已不含sinE项。将式(19)、式(20)代入式(16),得到由径向S(t)、横向T(t)控制加速度引起的近地点幅角的变化率:
(21)
因此,关于对式(14)所对应的最优径向、横向加速度S*(t)和T*(t)的求解,最终转换为对满足式(15)约束的最优N*(t)的求解。
2.2 解析控制方程
N(t)为在一个轨道周期内的时变函数。对于N*(t)的求解,最直观的方法是利用各类优化算法进行迭代以取得最优解,但该方法需要较大的计算量,对于星上计算机是不可接受的。较为可行的方法是对问题进行简化,通过牺牲少许的最优性,以期得到一个具有解析形式的最优解。直观上看,对卫星轨道实施的控制力往往具有与轨道运行周期相关的周期性,因此,本文将N(t)展开成轨道偏近点角形式的傅里叶级数,截取合适的阶次,将轨道优化问题转变为计算量较小的参数优化问题,得到N(t)的次优解。N(t)可表示为
(22)
式中:m为函数N(t)所截取的阶数。
当假定卫星具有大容量蓄电池,可以在卫星进入地影区时保证推力器能够正常工作,并且也不存在其他任务对电推力器的点火进行约束,能够实现推力器的常开点火。在此前提下,可直接对式(14)、式(15)在0~2π之间进行积分。由此,当式(22)截取的阶数够短时,可得到形式非常简单的解析解。
当N(t)仅取0阶,即N(t)为常数项时,仅存在一个待求解参数a0,可求得满足式(16)约束的解
(23)
该解仅满足式(16)的约束,但无足够的自由度对控制力进行一定程度的优化。
当N(t)仅取1阶时,N1(t)可写为
N1(t)=a0+a1cos(E(t))+b1sin(E(t))
(24)
则式(15)可表示为
a1(3e2+8e+4)]
(25)
联立式(14)和式(25),可得到由a1、b1表示的目标函数J(a1,b1)。J(a1,b1)的极小值需要求解下列方程:
(26)
由式(25)、式(26)可解出:
(27)
(28)
(29)
其中,k(e)=640+960e+496e2+256e3+236e4+28e5-61e6-17e7+12e8,g0(e)=208+216e+56e2+54e3+42e4-9e5+3e6,g1(e)=48+40e+8e3+11e4-2e5。
当偏心率为小量时,可将上式进一步简化,略去e4阶及以上小量:
(30)
(31)
(32)
如图2所示,略去4阶以上小量对系数影响很小。

图2 未简化系数与略去小量系数曲线Fig.2 The originand simplified values of and
当Nm(t)所截取的阶次每增加一阶,待求的参数也随之增加2个,需要利用到数值解法,进行迭代求解。图3为采用单纯形数值搜索方法,Nm(t)截取阶数为1~4阶时在一个轨道周期内燃料消耗与零阶N0(t)的比值。从图3中可见,随着卫星的轨道偏心率的增大,增加函数Nm(t)的阶次,即增加更多的待优化参数,越能够降低控制的燃料消耗,但随着阶次的提高,降低燃料消耗的效果越不明显。但事实上,仅截取到一阶函数进行优化,即可节省足够的燃料。此时存在解析解式(27)~ (29)。但值得注意的是,即使Nm(t)取到足够高的阶数,也并不是最优化问题式(14)~(18)的最优解。但对于有条件利用地面高性能计算机进行大量迭代计算的情况下,Nm(t)显然也可以作为最优解N*(t)的初始猜测。
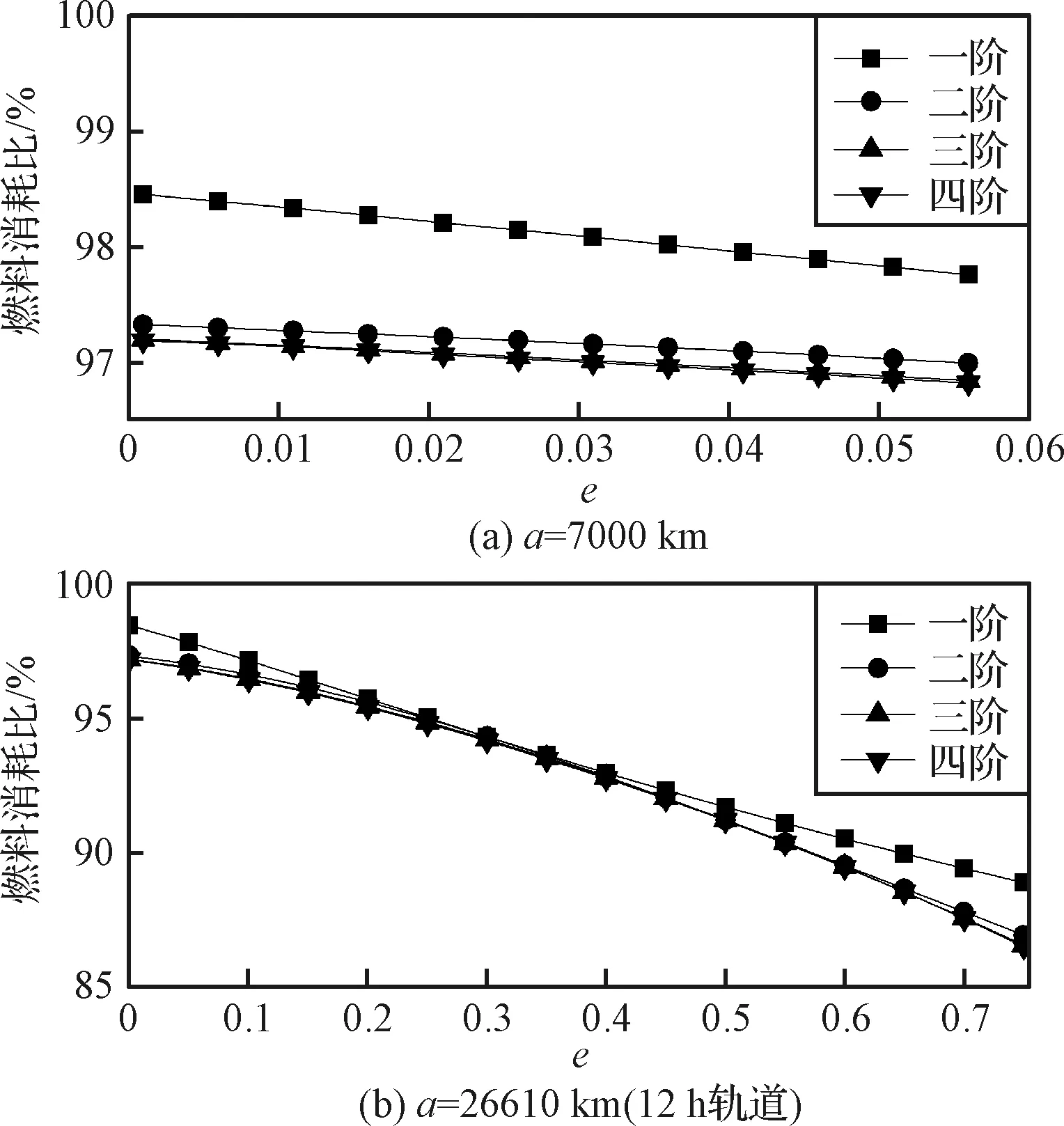
图截取阶数与零阶燃料消耗比Fig.3 The ratio of fuel consumption of to N0(t)
综上所述,本文提出的控制方式的计算步骤如下:
1)根据目标值和自然摄动计算所需的近地点幅角控制量Δω。
2)根据截取的Nm(t)阶次,计算Nm(t)的系数a0,a1,b1,…,am,bm。
3)计算轨道周期内的横向、径向控制量S(t)和T(t)。
为得到燃料消耗更小的结果,本文提出的方式仅考虑对近地点半径rp进行约束,半长轴和偏心率会发生变化。因此在每个轨道周期阶数后,要重新调用以上步骤,对下一轨道周期内的控制量S(t)和T(t)进行计算。

3 仿真校验
为对本文提出方法的正确性进行检验,本文给出了利用连续小推力策略对卫星远、近地点进行控制的三个仿真算例。算例1为低轨用于对地观测的小偏心率椭圆轨道卫星近地点星下点全球覆盖速率进行人工控制;算例2为对闪电轨道的拱线进行小推力控制;算例3为水星环绕轨道对某一纬度范围带的反复探测控制。
3.1 算例1:近地点全球覆盖控制
算例1的初始条件详见表1。对于该组轨道根数,对近地点星下点纬度(即近地点幅角)影响最大的因素是J2项非球形摄动,其自然近地点幅角变化率为-3.274(°)/d,因此近地点星下点对全球的覆盖周期为110 d。本算例的目标是使目标星下点覆盖周期缩短为60 d,即将近地点幅角的变化率控制到-6(°)/d。为此,轨道动力学模型考虑四级四阶地球非球形引力和日月第三体引力摄动,并采用四阶定步长RK法进行数值积分,仿真时长为60 d。

表1 初始条件(算例1)Table 1 Initial conditions of example 1
仿真结果如图4~图6所示。由图4可知,在整个全球覆盖小推力控制过程中,卫星近地点的星下点纬度实现了在除南、北极外[-90°,90°]区间内的周期性变化,星下点经度由地球自转影响能够密集覆盖[-180°,180°]。由图5可见,在对卫星近地点覆盖性进行人工控制期间,合并受到其他轨道摄动力的影响,卫星近地点高度的变化幅度在30 km范围内,远地点高度在50 km变化,较为稳定。图6为卫星控制力曲线,对于质量为1000 kg的卫星,轨道系X轴方向的控制力在[-0.1 N,0.1 N]以内,Z轴方向的控制力在[0 N,0.45 N]之间,每轨均呈周期性变化。假设利用太阳能电推进系统实现近地点覆盖控制,比冲为3000 s,在整个覆盖控制周期(60 d)的总燃料消耗为49.5 kg,对于紧急任务和强机动卫星来说是可以接受的量级。

图4 卫星近地点星下点纬度、经度(算例1)Fig.4 Longitude and latitude of satellite perigee (example 1)

图5 卫星远地点、近地点高度(算例1)Fig.5 Orbit altitude of satellite apogee and perigee (example 1)

图6 卫星控制力曲线(算例1)Fig.6 Control force of satellite with 60 days (example 1)
3.2 算例2:闪电轨道拱线控制
在闪电轨道上运行的卫星多为为特定纬度地区服务的通信卫星,星上载荷工作范围多为在远地点附近。算例2的初始条件详见表2。初始近地点幅角为-90°,即远地点星下点位于北纬。由于轨道高度较高,卫星近地点幅角、升交点赤经的自然漂移速率≈0。本算例的目标是使目标远地点星下点纬度由原先的63.4°(ω0=-90°)在7.5天内遍历至41°附近,即为将近地点幅角的变化率控制到6(°)/d。为此,轨道动力学模型考虑四级四阶地球非球形引力和日月第三体引力摄动,并采用四阶定步长RK法进行数值积分,仿真时长为7.5 d。

表2 初始条件(算例2)Table 2 Initial conditions of example 2
仿真结果如图4~图9所示。由图4可知,在整个过程中,卫星远地点的星下点纬度由最高的63.4°逐渐变换至41°附近。由于卫星轨道周期与地球自转存在整数关系,星下点经度主要活动于两个特定区域。由图8所示,卫星近地点高度的变化幅度在30 km范围内,远地点高度在1000 km变化,较为稳定。由图9所示,对于质量为1000 kg的卫星,对闪电轨道的控制力较大,轨道系X轴方向的控制力在[-0.5 N,0.5 N]以内,Z轴方向的控制力在[0 N,7.5 N]之间,每轨均呈周期性变化。假设利用大功率电推进系统实现近地点覆盖控制,比冲为6000 s,在仿真时长内的总燃料消耗较大,为57.0 kg,但鉴于该轨道可以改变通信卫星服务的纬度范围,燃料消耗依旧小于重新发射新的卫星。

图7 卫星远地点星下点纬度、经度(算例2)Fig.7 Longitude and latitude of satellite perigee (example 2)

图8 卫星远地点、近地点高度(算例2)Fig.8 Orbit altitude of satellite apogee and perigee (example 2)

图9 卫星控制力曲线(算例2)Fig.9 Control force of satellite (example 2)
3.3 算例3:水星环绕轨道控制
在本算例中,提供了文中算法更为灵活的应用方式。算例选为水星附近的深空环绕轨道,初始条件详见表3。本算例进行控制的目的是在30 d的探测周期内,在前15 d航天器的近地点由北极附近过渡到赤道附件,后15 d再由赤道过渡回北极。采用四阶定步长RK法进行数值积分,仿真时长为30 d。

表3 初始条件(算例3)Table 3 Initial conditions of example 3
仿真结果如图10~图12所示。近地点的星下点纬度实现了[0,75°]区间内反复变化。在对卫星近地点覆盖性进行人工控制期间,合并受到其他轨道摄动力的影响,卫星近地点高度的变化幅度在15 km范围内,较为稳定。对于质量为500 kg的探测器,轨道系X轴方向的控制力在[-0.2,0.2]N以内,Z轴方向的控制力在[-1.2,1.2]N之间,每轨均呈周期性变化。假设利用太阳能电推进系统实现近地点覆盖控制,由于距离太阳极近,系统功率很大,比冲为5000 s以上,在整个控制过程中的总燃料消耗为48 kg,对于深空探测来说是可以接受的量级。

图10 卫星远地点星下点纬度、经度(算例3)Fig.10 Longitude and latitude of satellite perigee (example 3)

图11 卫星远地点、近地点高度(算例3)Fig.11 Orbit altitude of satellite apogee and perigee (example 3)

图12 卫星控制力曲线Fig.12 Control force of satellite (example 3)
4 结 论
本文针对椭圆形对地服务航天器的星下点覆盖性控制问题,提出了基于连续小推力的控制策略,在不破坏卫星近地点高度的基础上,通过对卫星轨道拱线的旋转速率的优化控制,实现对地面星下点覆盖周期的调整,最后给出了仿真算例和结果。仿真结果表明,本文提出的方法能够有效、安全地实现对卫星近/远地点全球覆盖速度的控制和特定纬度区域的推扫,燃料消耗在一定范围之内。

