高速SpaceWire协议IP的可靠性增强方法

姜 宏，杨孟飞，刘 波，刘鸿瑾，龚 健

(1. 北京控制工程研究所，北京 100190； 2. 中国空间技术研究院，北京 100094)

0 引 言

SpaceWire[1]是由欧空局和英国Dundee大学于2000年共同制定的航天总线标准。该标准于2003年、2005年、2008年和2010年经过了多次更新和补充后形成目前较完善的标准体系。在SpaceWire标准的基础上，本文在前期工作中研制了高速SpaceWire协议IP[2]，将200 Mbps的传输速率提速到1 Gbps以上，可满足高速数据传输的需求。但是，作为一种航天数据总线，除了要满足高速传输要求外，更重要的是保证系统的可靠性。

总线系统的可靠性一方面取决于协议本身的检错和纠错能力，另一方面取决于实现环节的技术手段。本文实现的高速SpaceWire协议IP，其物理载体是SRAM型的FPGA芯片。由于空间辐照作用，这种FPGA芯片如果在空间工作极易受到单粒子翻转效应(Single event upset,SEU)的影响而导致功能失效，从而使系统可靠性显著下降。为解决这个问题，国内外学者提出了很多针对SRAM型FPGA的抗辐射加固容错技术[3-6]，从空间、时间等多个维度开展冗余设计，提高系统容错能力。在这些技术中，三模冗余(Triple modular redundancy，TMR)[7-8]是最具有代表性的。

三模冗余方法首先由冯·诺依曼于1956年提出，核心思想是将原设计克隆出三份，每一份都单独工作并输出一组信号，然后对三组输出信号进行三取二表决，最后给出表决后的输出结果。

传统TMR方法对于系统可靠性虽然有较大的改善，但是付出的资源代价和获得的可靠性之间的性价比不高。因此，研究人员提出了选择性三模冗余(Selective TMR)[9]和部分三模冗余(Partial TMR)[10]。在这类方法中，部分三模冗余(又被称为分层三模冗余[11-12])最具有代表性，其特点是以更细的粒度开展设计，将原设计切割为多个部分或阶段，对每个部分做三模冗余，从而形成一系列三模冗余子系统。虽然部分三模冗余会提高系统可靠性，但是如果划分过细，数量庞大的表决器会成为系统可靠性的薄弱点，导致可靠性不升反降，因此表决器的数量不宜过多。

TMR虽然能够在短时间内对单个故障进行容错，但是随着时间的推进会发生错误的累积，进而导致多个故障的发生，TMR方法会因此失效。于是针对SRMA型FPGA的加固设计，学者们提出了具有自刷新能力的TMR[13]，从而能够保证在很长的时间内系统可靠运行。

然而，随着航天器电子系统的通信和处理速度的不断加快，FPGA等电子元器件的工作频率越来越高，对空间辐照的影响越来越敏感，另外国内外航天器的在轨寿命有不断延长的趋势，对包括SpaceWire协议IP在内的FPGA逻辑设计的可靠性提出了更高要求。为满足之一要求，一种方法是缩短FPGA模块的刷新周期提高故障维修率，但是如果单纯提高刷新频率，会导致电子系统的功耗明显增加，并且还会使系统的实时性变差。

为此，本文提出了一种针对SRAM型FPGA的TMR新方法——增强三模冗余(Enhanced TMR，ENTMR)，该方法能够在不缩短刷新周期的前提下,有效提高高速SpaceWire协议IP设计的可靠性。

1 增强三模冗余

1.1 基本方法

在航天数据总线系统中，每个FPGA功能单元(简称单元)的故障率不是完全相同的，存在着一些可靠性薄弱点。假设系统的某个单模FPGA设计M共包含三个单元A,B,C(如图1所示)，其中A和B的输出是C的输入，并设B单元是易发生故障的关键单元(阴影线区域)。

图1 原设计功能结构Fig.1 Function structure of original design

对于图1所示的系统，传统TMR不会对关键单元进行区分，只是简单的对原设计M整体做三模冗余设计。部分TMR有两种策略：一种策略是只对关键单元做三模冗余，一般单元仍然是单模，这时虽然节省了资源，但牺牲了系统可靠性；另一种策略是对关键单元和一般单元都做三模冗余，这时对两种单元的加固方法是一样的，并未提供对关键单元的额外防护。

本文方法与TMR和部分TMR的不同点在于：不仅对一般单元做三模冗余，而且对关键单元做四模冗余[14]。对于单一信号的多模冗余，传统四模冗余与三模冗余在FPGA两次刷新之间都只能容忍1个故障，并无明显优势，因此本文在此基础上，借鉴故障顺序出现情况下的系统诊断方法[15]，提出了顺序四模冗余(Sequential quad modular redundancy，SQMR)，从而能够使关键单元容忍的故障数大于1。

图2 增强三模冗余示例Fig.2 Example of enhanced TMR

图2是增强TMR方法的一个示例，在该例子中对图1中的一般单元A和C都做三模冗余，对关键单元B做顺序四模冗余。顺序四模冗余要正常工作需满足以下前提条件：

假设条件1. 在FPGA的相邻两次刷新之间，四模(例如图2中的B1、B2、B3、B4)中两个或两个以上单元几乎同时出错的概率近似为0。

当具备上述条件后，N模冗余(NMR)容错系统能容忍的故障数t与N不必满足N≥2t+1[16]，从而当N=4时，可容忍的故障数t可以大于1，方法如下：

(1)若在FPGA的相邻两次刷新之间，四模冗余结构中只有一个单元发生故障，则显然可通过多数原理进行容错；

(2)若在FPGA的相邻两次刷新之间，有两个单元先后出错，则当第一次错误出现时，可通过4选3排除，当第二次错误出现时，又可通过3选2排除。

为了防止错误累积，增强TMR系统还包含故障检测模块和FPGA的配置刷新(Configuration scrubbing)模块。配制刷新对于提高SRAM型FPGA的可靠性非常重要，正如文献[17]所强调的，如果FPGA不进行配置刷新，当多模冗余系统工作超过一段时间后，其可靠度会低于单模系统。

1.2 ENTMR的优势

ENTMR系统中的主体部分是一般单元集，由于主体部分依然采用三模冗余方法，因此下面以传统TMR和部分TMR作为参照来说明ENTMR的优势。

在如图3所示的例子中(下划线表示该路信号出错)，在FPGA模块两次刷新之间，M1中的关键单元B1出错，M2中的关键单元B2出错，从而M1和M2的输出OC1和OC2都出错，最终导致三模冗余方法失效。

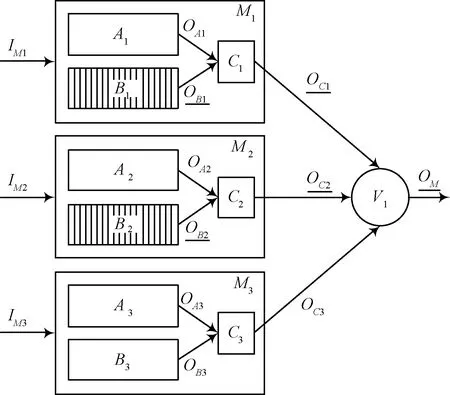
图3 三模冗余失效情况Fig.3 Fault case of TMR

如果采用部分三模冗余结构(如图4所示，下划线表示该路信号出错)，将原设计M拆分为三部分，即：每个单元就是一个细分部分，然后对各部分做三模冗余，相应的表决器有三个分别为V1，V2和V3。接下来假设关键单元B1和B2出错，则OB1和OB2出错，从而导致经表决器V2输出的OV2出错，因此部分三模冗余方法失效。

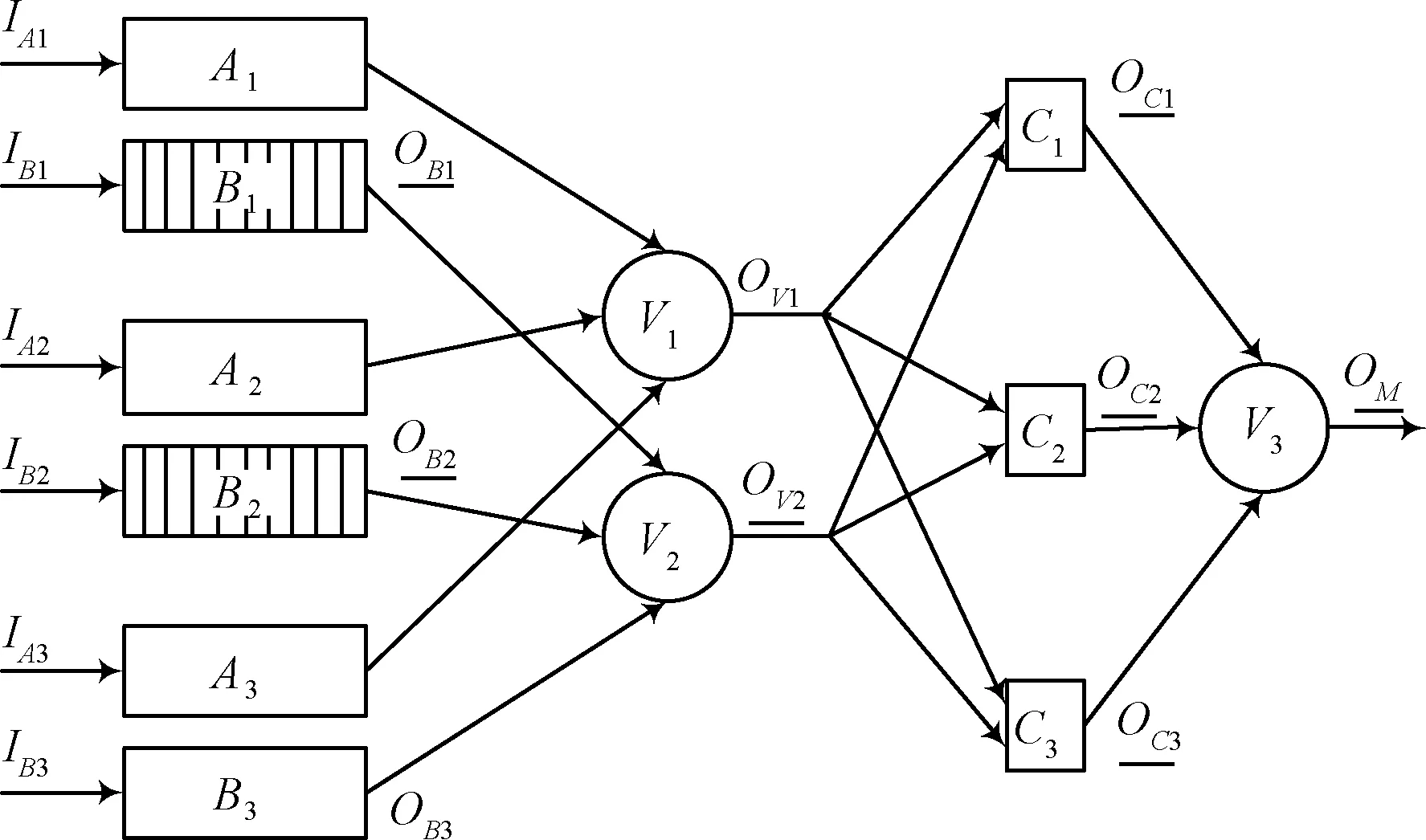
图4 部分三模冗余失效情况Fig.4 Fault case of partial TMR

由于增强TMR对关键单元做顺序四模冗余，则按照图2所示的结构，能够在B1和B2先后出错的情况下避免OB出错，从而确保OM信号正确。

1.3 表决器

ENTMR方法的实现离不开表决器设计。本文ENTMR的表决器分为两种：TMR表决器和SQMR表决器。

一般单元集内的每个单元采用TMR表决器[18]，如图2中的表决器V1，其布尔表达式为：

VTMR=AB+AC+BC

(1)

式中:VTMR为TMR表决器的输出，A,B,C为TMR结构中的三个同构单元的输出并作为TMR表决器的三个输入。

关键单元集中的每个单元采用SQMR表决器，如图2中的表决器V2，其布尔表达式为：

VSQMR=F1F2F3F4(ABC+ABD+

BCD)+F1F2F3(AB+AC+

BC)+F1F2F4(AB+AD+

BD)+F1F3F4(AC+AD+

CD)+F2F3F4(BC+BD+

CD)+……

(2)

其中，Fi(i=1, 2, 3, 4)是四个单元中第i个单元的无故障标志。若Fi=1，表示未检测出第i个单元发生故障，若Fi=0，表示检测出第i个单元发生故障。由于这些标志的存在，因此本文顺序四模冗余的表决器是一种基于标志的SQMR表决器。这些标志信号可由故障检测模块提供。

式(2)与式(1)相比虽然表面上复杂度明显增大，但是应注意到式(2)中的标志信号及相关布尔运算在带有故障检测模块的系统中原本就已存在，这里只是在表决器中引进来加以利用，并未多占资源。因此，实际上SQMR表决器新占的资源在QMR和TMR的基础上增加有限。

2 可靠性比较

本文在进行传统TMR、部分TMR和ENTMR方法的可靠性比较时考虑到传统TMR方法的可靠性不高于部分TMR方法，且ENTMR与部分TMR对于一般单元的处理方式是相同的，因此将重点放在针对关键单元的SQMR和TMR的可靠度的计算和比对上。

对于TMR系统，设系统中每个冗余单元的可靠度为Rm(t)，则系统可靠度Rst(t)为：

(3)

对于SQMR，同样假设每个冗余单元的可靠度为Rm(t)，则系统可靠度Rss(t)为：

(4)

(5)

由式(3)和式(5)可得：

(6)

为了便于分析，将式(6)中的Rm(t)用x代替，并令该式为L(x)有：

L(x)=3x2-6x3+3x4

(7)

由于L(x)在(-∞, +∞)内一阶可导，因此得到：

L′(x)=6x-18x2+12x3=6x(2x-1)(x-1)

(8)

分析式(8)可知，L(x)在x= 0.5处取得极大值，在x= 0和x= 1处取得极小值，从而当x∈[0, 1]时，0.1875 ≥L(x) ≥ 0，即：

0.1875≥Rss(t) -Rst(t) ≥ 0

(9)

式(9)是关于关键单元的顺序四模冗余和三模冗余方法的可靠度差值，同时也是ENTMR方法和部分TMR方法的可靠度的一般比较结果。但是不够充分和直观，下文将通过仿真方法给出进一步的结果。

3 可靠性仿真

前文已提到，为了提高三模冗余设计的可靠性，本文采用了自刷新机制，从而使系统具备可维修能力。

由于电子系统(包含FPGA)发生故障的统计规律近似服从指数分布，在发生故障后可通过刷新进行故障维修，并且各模块的维修时间也近似服从指数分布，因此构成了一个马尔科夫可修系统[19]。

基于马尔科夫可修系统的可靠性计算和仿真方法在电子系统中的应用已经比较成熟，下面将采用该方法首先建立增强三模冗余系统、传统三模冗余系统和部分三模冗余系统的可靠性模型，然后进行仿真分析和结果对比。

3.1 增强TMR的可靠性模型

在对系统进行可靠性建模和仿真分析时，由于包含多个关键单元和多个一般单元与包含1个关键单元和1个一般单元的方法和过程基本一致，为便于描述和计算这里只考虑原设计包含1个关键单元和1个一般单元的情况。则经冗余后，系统共包含4个关键单元和3个一般单元。在此情况下，增强三模冗余系统运行的状态空间包含如表1所示的7种状态：

表1 增强三模冗余系统状态和相关说明Table 1 System states of ENTMR and related descriptions

在表1中，0、1、2、3、4、5都是未失效状态，状态6是系统失效状态。

设关键单元Ek在单位时间的失效次数(简称为失效率)为λ1，一般单元En的失效率为λ2，某个单元的单位时间维修次数(简称为维修率)为μ，再设在很短的时间Δt内只会有一个单元发生故障，在Δt时间内只能通过刷新修复一个单元的故障(因为部分重配置过程也需要耗费一定时间)，则各个状态之间的状态转换如图5所示：

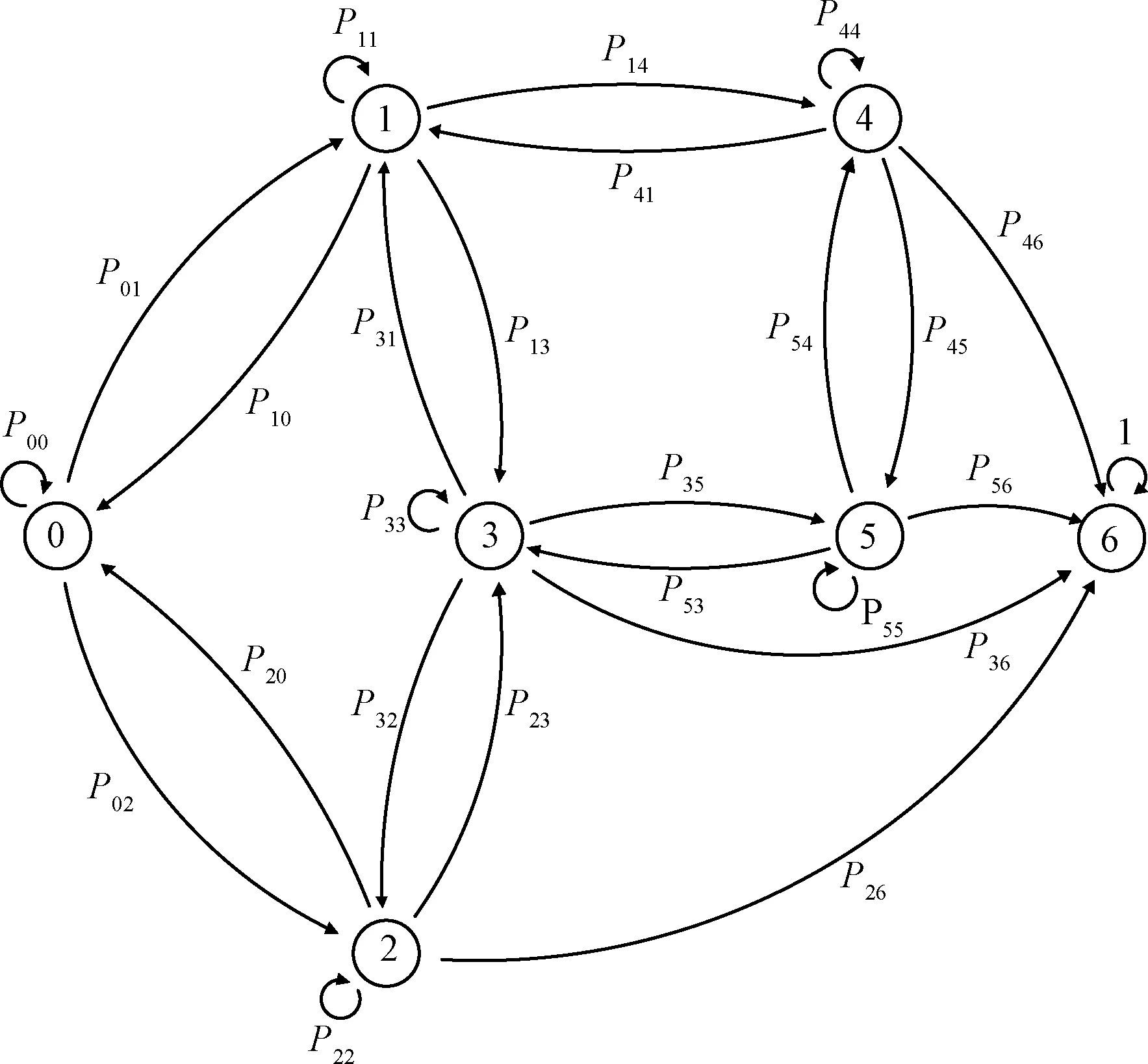
图5 增强TMR的状态转换图Fig.5 State chart of ENTMR

图5中，各状态之间的转移概率如表2所示：

表2 转移概率Table 2 Transition probability

注.由于某个单元发生故障的概率分布近似服从指数分布，且维修时间也近似服从指数分布，故当Δt很小时，某单元在t时刻失效，在t+Δt时刻被修复的概率为1-e-μΔt，近似为μΔt，某个Ek单元和En单元在t时刻正常，在t+Δt时刻发生故障的概率分别为：1-e-λ1Δt和1-e-λ2Δt近似为λ1Δt和λ2Δt。

1)状态转换图说明

在图5中，状态0为系统的初始状态，此时不论是关键单元还是一般单元都没有发生任何故障。在此状态下，当有一个Ek发生故障后，进入状态1，当有一个En发生故障后，进入状态2。

在状态1下，若有一个En发生故障，则系统进入状态3，若有另一个Ek发生故障，则系统进入状态4，若故障被修复则系统进入状态0，否则停留在状态1。

在状态2下，若有一个Ek发生故障，则系统进入状态3，若有另一个En发生故障，则系统进入状态6，若故障被修复则系统进入状态0，否则停留在状态2。

在状态3下，若又有Ek发生故障，则系统进入状态5，若又有En发生故障，则系统进入状态6，若Ek的故障被修复则进入状态2，若En的故障被修复则进入状态1，其他情况下停留在状态3。

在状态4下，若又有En故障，则系统进入状态5，若又有Ek故障，则系统进入状态6，若故障被修复则系统进入状态1，否则停留在状态4。

在状态5下，若又有En故障或Ek故障，则系统进入状态6，若有一个Ek的故障被修复则进入状态3，若En的故障被修复则进入状态4，否则停留在状态5。

在状态6下，系统以概率1停留在状态6。

2)Ek数为1的ENTMR系统可靠性计算

令增强三模冗余系统在t时和t+Δt时处于状态0、状态1、状态2、状态3、状态4、状态5、状态6的概率分别为：Pe0(t),Pe1(t),Pe2(t),Pe3(t),Pe4(t),Pe5(t);Pe6(t)，Pe0(t+Δt);Pe1(t+Δt);Pe2(t+Δt),Pe3(t+Δt),Pe4(t+Δt),Pe5(t+Δt),Pe6(t+Δt)，则由表2可列出状态转移矩阵为：

(10)

再由系数矩阵Be=Ae-I(I为7阶单位阵)可得到系统的状态微分方程组为：

(11)

微分方程组(11)的初始条件为t= 0时系统未发生任何故障，即：Pe0(0)=1，Pe1(0)=0，Pe2(0)=0，Pe3(0)=0，Pe4(0)=0，Pe5(0)=0，Pe6(0)=0。

根据式(11)及初始条件求解出微分方程组的解，并得到关键单元个数为1时的增强TMR的可靠度Re(t)为：

Re(t)=Pe0(t)+Pe1(t)+Pe2(t)+

Pe3(t)+Pe4(t)+Pe5(t)

(12)

3.2 传统TMR的可靠性模型

传统三模冗余系统运行的状态空间包含如表3所示的3种状态：

表3 传统TMR系统状态和相关说明Table 3 System states of TMR and related descriptions

在表3中，状态0和状态1是未失效状态，状态2是系统失效状态。当超过两个单元发生故障时，系统进入状态2。

设每个单元的失效率为λt，维修率为μ，同样设在很短的时间Δt内只会有一个单元发生故障，在Δt时间内只能通过刷新修复一个单元的故障。令传统三模冗余系统在t时和t+Δt时处于状态0、状态1、状态2的概率分别为：Pt0(t),Pt1(t),Pt2(t),Pt0(t+Δt),Pt1(t+Δt),Pt2(t+Δt)，由文献[20]可得到TMR系统的状态微分方程组为：

(13)

微分方程组(13)的初始条件为t= 0时系统未发生任何故障，即：Pt0(0)=1，Pt1(0)=0，Pt2(0)=0。

根据式(13)及初始条件对微分方程组求解，可得到传统三模冗余系统的可靠度Rt(t)为：

Rt(t)=Pt0(t)+Pt1(t)

(14)

3.3 部分TMR的可靠性模型

与增强TMR类似，这里也只考虑将原设计分割为2个单元时的情况。设单元1的失效率为λp1，单元2的失效率为λp2。再设部分TMR系统中由单元1构成的TMR子系统的可靠度为Rp1(t)，由单元2构成的TMR子系统的可靠度为Rp2(t)，所有故障单元的维修率都为μ。

若部分三模冗余系统包含多个TMR子系统，则只有在所有子系统都可靠的时候系统才可靠。因此，对于包含2个TMR子系统的部分TMR系统，其可靠度Rp(t)为：

Rp(t)=Rp1(t)·Rp2(t)

(15)

3.4 模型仿真及结果分析

因为方程组(11)和(13)中存在多个不确定的参数不易直接得到解析解，所以本文在开展仿真时首先根据模型设定一组参数，然后利用MATLAB软件在给定参数下求解方程组，得到方程组(11)和(13)的结果，再由(12)、(14)和(15)计算出增强TMR、传统TMR和部分TMR的可靠度数值。

对于增强TMR将原设计分割为一个关键单元(Ek)和一个一般单元(En)，对于部分TMR不区分关键单元只是将原设计分割为两个部分(这两部分的失效率分别为λp1和λp2)。现在设原设计的失效率为λt，由于整体和局部的失效率的关系为：

1-λt=(1-λp1)(1-λp2)=(1-λ1)(1-λ2)

(16)

当λ1,λ2,λp1,λp2都很小时，λp1λp2和λ1λ2相对可忽略，于是近似有：

λt=λp1+λp2=λ1+λ2

(17)

在仿真参数设置上，取λt=0.0002/h，维修率μ=0.8/h。根据式(17)将λt进行分配，设参数λ1=0.00012/h,λ2=0.00008/h,λp1=λp2=0.0001/h。

仿真时间从0开始，到180000 h结束，各个时间点分别设置为：0 h,10000 h,20000 h,30000 h,40000 h,50000 h,60000 h,70000 h,80000 h,90000 h,100000 h,110000 h,120000 h,130000 h,140000 h,150000 h,160000 h,170000 h,180000 h。

根据上述设置(参数设置1)，运行仿真后得到的可靠度数据如表4所示。

通过表4的数据可发现，随着系统运行时间的延长，三种方法的可靠度都在下降，但是增强TMR的可靠度下降速度最慢，部分TMR的可靠度下降速度约为增强TMR的3倍，传统TMR的可靠度下降速度约为增强TMR的6倍。当仿真运行到180000 h处时，增强TMR的可靠度最高，部分TMR的可靠度略低，传统TMR的可靠度最低，且增强TMR的可靠度比传统TMR高4.63%，比部分TMR高1.70%。如果航天器总体下达的任务期末的可靠度要求为0.975，则在此仿真条件下传统TMR只能按要求工作9年，部分TMR为19年，增强TMR则能轻松超过40年。

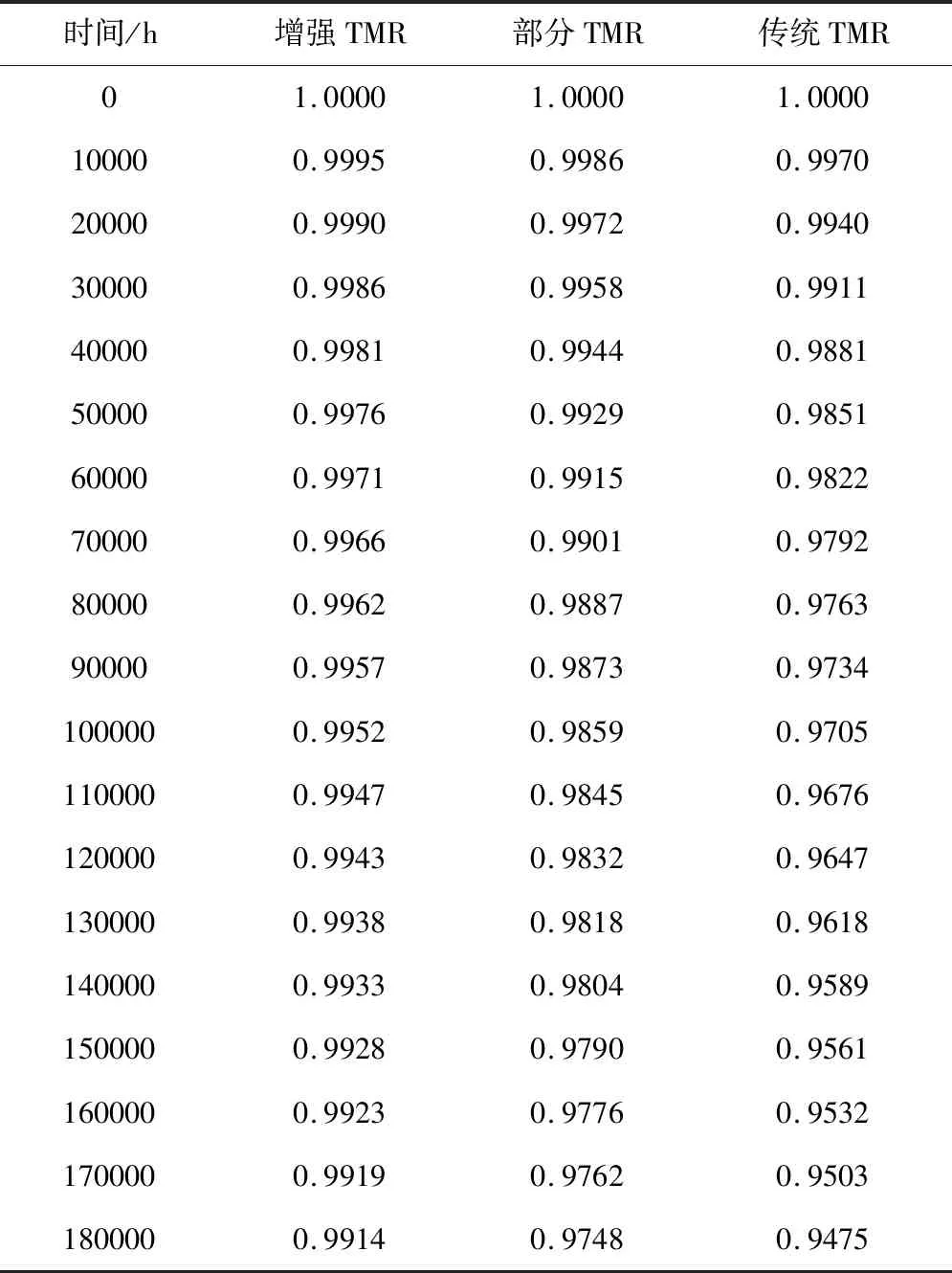
表4 三种方法的可靠度对比Table 4 The comparison of three methods

由于增强TMR和部分TMR的可靠度较为接近，为了更直观地将这两种方法的可靠度进行对比，将仿真参数按三种情况(Case1,Case2,Case3)进行设定，在运行仿真360000 h后取二者可靠度之差与部分TMR可靠度原值的比值δ(t)(δ(t)=(Re(t)-Rp(t))/Rp(t))绘制了如图6所示的点图。

图6 三种仿真参数下的δ(t)点图Fig.6 The δ(t) plots under three parameters

δ(t)值越大反映的是增强TMR系统相比部分TMR系统的可靠性优势越大。由图6可知，随着时间t的变化，δ(t)的数值不是固定不变的，而是呈现出逐渐增大趋势，这说明运行时间越久增强TMR方法的可靠性优势越显著。在Case1下，增强TMR系统的360000 h可靠度比部分TMR略高(约为1%)；在Case2下，增强TMR的360000 h可靠度比部分TMR高3%以上；在Case3下，增强TMR系统的360000 h可靠度比部分TMR高15%以上。上述结果表明：当原设计的可靠性很高时，可靠度的提高不明显，但是当原设计的可靠性较低时，增强TMR系统能获得明显高于部分TMR的可靠度。这充分说明了增强TMR方法比部分TMR更适用于空间恶劣环境。

4 结 论

本文在传统三模冗余和部分三模冗余的基础上提出了增强三模冗余方法。该方法将原设计分割为一般单元集和关键单元集，对一般单元集的每个单元做三模冗余，对关键单元集的每个单元做顺序四模冗余。通过这种混合冗余结构，使高速SpaceWire系统和薄弱单元的可靠性得到增强。

本文在提出ENTMR方法后给出了系统可靠性的计算公式和表决器的布尔表达式。在此基础上，为了对增强三模冗余系统的可靠性进行论证，首先针对典型场景(系统中包含1个一般单元和1个关键单元)建立了具有维修能力的增强三模冗余系统的马尔科夫可靠性模型，并基于该模型利用MATLAB软件开展仿真运算，获得了系统可靠度的仿真数据。然后根据传统TMR和部分TMR的马尔科夫可靠性模型开展MATLAB仿真，又获得了两组可靠度仿真数据。接下来将三组数据进行对比，得到如下结论：

1)增强TMR系统的可靠度不仅明显高于传统TMR，而且高于部分TMR。

2)在参数设置1和任务期末的可靠度要求为0.975的条件下，增强TMR系统的正常工作寿命是部分TMR系统的2倍多，是传统TMR系统的4倍多。

最后按照三种参数设置运行仿真，对增强三模冗余系统和部分三模冗余系统的可靠性进行了重点比较，仿真结果显示：当原设计的可靠性较低时，增强TMR系统能获得明显高于部分TMR系统的可靠度，在仿真参数Case3下，仿真运行到360000 h后，增强TMR系统比部分TMR系统的可靠度高15%以上，效果显著；当原设计的可靠性较高时，增强TMR系统的可靠度虽然高于部分TMR系统，但效果并不明显。上述仿真结果同时验证了式(9)的正确性。