基于粒子群优化核极限学习机的北斗超快速钟差预报

李文涛,边少锋,任青阳,梅长松,潘 雄

(1.中国地质大学(武汉)地理与信息工程学院，武汉 430074; 2.重庆交通大学土木工程学院，重庆 400074)

0 引言

在全球导航卫星系统(Global navigation satellite system，GNSS)实时导航定位中，星载原子钟的钟差预报在优化导航电文中的钟差参数、满足实时动态精密单点定位的需求、提供卫星自主导航所需的先验信息等方面具有重要的作用[1]。目前，我国自主研发的北斗系统已进入全球组网新时代，应用产业呈现快速发展，但是大多数北斗卫星上配备的国产铷钟的频率稳定性相对较差，国际GNSS监测评估系统(International GNSS monitoring & assessment system，iGMAS)提供的超快速钟差的预报产品精度较低(10 ns内)，在一定程度上限制了北斗实时精密导航定位的应用[2]。因此，北斗卫星钟差的实时精密确定与短期高精度预报已成为高精度实时导航应用中的关键技术之一。

由于卫星原子钟自身的时频特征较为复杂且外界环境容易对原子钟产生影响，从而在卫星钟差时间序列中存在着周期性变化和随机性变化[2]，许多学者常采用多项式[3]和周期项[4]模型进行预报，采用多项式模型预报钟差时，其预报误差会随着预报时间的增加而逐渐变大，周期项模型的显著周期需要根据较长的钟差序列才能较为准确地确定。由于这些非线性特性较为复杂，使得这些方法并不能很好地表示钟差时间序列的非线性特性[5]。因此，一些学者提出了人工智能方法，如BP神经网络法[2,6]和最小二乘支持向量机法[7,10]等，相比于多项式模式和周期项模型有一定的提升效果，但仍存在一些不足。

针对神经网络模型的不足，Huang[8]等提出了一种新型的单隐层前馈神经网络，称为极限学习机(Extreme learning machine，ELM)，ELM采用正则化最小二乘原理调节输出权值矩阵，使得网络的训练速度和泛化性能得到了极大的提高。但是，ELM需要预先确定隐含层节点的数目，此时有学者在ELM的基础上，提出了一种核极限学习机(Kernel extreme learning machine，KELM)模型[9]，将隐含层节点映射用核函数映射替代,通过选择合适的核参数与正则化系数，进而计算网络的输出权值矩阵。本文引入粒子群优化算法(Particle swarm optimization，PSO)[10]来选择核极限学习机所需的核参数与正则化系数，从而将PSO和KELM二者相结合，建立了基于粒子群优化核极限学习机(PSO-KELM)的预报模型，并将该方法应用到超快速钟差预报中，给出了相应的超快速钟差预报步骤，用iGMAS提供的实测北斗超快速钟差数据对算法的有效性进行了测试验证。

1 PSO-KELM基本原理

1.1 KELM算法

给定N个训练样本(xi,ti)∈Rn×Rm,i=1,2,…,N，其中xi为样本的输入，ti为样本的输出，ELM的隐含层节点数为L，激励函数为g，则其网络节点的输出为：

(1)

式中：βj为第j个隐含层节点和输出节点之间的权重值，wj为第j个隐含层节点和输入节点之间的权重值，bj为第j个隐含层节点的偏置。ELM算法随机选择隐含层节点的输入权重和偏置，基于最小二乘法原理计算输出隐含层节点到输出节点的权重值，因此该算法的学习速度非常快。

可以将式(1)写成矩阵的形式如下：

T=Hβ

(2)

式中：H为隐含层节点输出矩阵，β为输出层权重矩阵，

ELM的网络学习过程为：

1) 随机选定隐含层节点的输入权重w和偏置b；

2) 计算出隐含层节点输出矩阵H；

3)计算输出层权重矩阵β=H+T(H+为输出矩阵H的Moore-Penrose广义逆)[11]。

注.当HHT的条件数很大时，HHT为奇异矩阵，为了避免系数矩阵病态对计算结果产生影响，引入正则化系数η,H+=HT(HHT+ηI)-1，当HHT为非奇异矩阵时，H+=HT(HHT)-1，即正则化系数为0。

结合式(2)，此时，ELM模型的网络输出函数为：

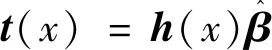
(3)

由于式(3)中的特征映射函数是未知的，可以用核函数映射代替随机映射，定义核函数矩阵为ΩELM=HHT，其中元素为ΩELM(j,i)=h(xj)·h(xi)=K(xj,xi)，相应的网络输出函数变为：

(4)

其中，核函数通常选择多项式核函数的形式[12]：

(5)

式中:p,q为多项式核函数的核参数。

1.2 PSO算法

从式(4)和式(5)可知，核参数与正则化系数的合理选择对于KELM算法的训练效果影响较大。在KELM超快速钟差预报模型中时，由于卫星钟差时间序列的非线性特性较为复杂，为了避免人为选择KELM参数的盲目性，可以利用粒子群优化算法(PSO)去选择适应钟差序列的核参数与正则化系数。

假设在d维空间中，一个粒子群由h个粒子组成，第i个粒子的速度和位置分别用Vi和Xi表示，Vi=[Vi1,Vi2,…,Vid],Xi=[Xi1,Xi2,…,Xid]，其中i=1,2,…,h，每个粒子的解就是其所在的位置。初始化时粒子的解是随机选取的，迭代时每个粒子通过确定两个极值解来更新自己：一个解称为个体极值，即粒子本身所找到的最优解；另一个解称为全局极值，即整个种群中的最优粒子解。主要迭代公式如下：

(6)

(7)

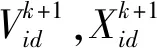
α=αmax-t(αmax-αmin)/tmax

(8)

式中：t表示当前迭代次数，tmax为最大迭代次数。

个体极值和全局极值的更新标准通常采用适应度[14]度量，其中适应度的计算公式如下：

(9)

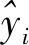
通过PSO算法确定出全局最优粒子解后，将粒子解映射为KELM最优的核参数和正则化系数，代入式(5)与式(4)中，即可得到最终的KELM预报模型表达式。

1.3 PSO优化KELM的超快速钟差预报方法

设超快速钟差数据为{x1,x2,…,xN}，用过去n个时刻的钟差值{x1,x2,…,xn}来预报n+1时刻的钟差值{xn+1}，即建立{x1,x2,…,xn}与{xn+1}的映射关系，再利用KELM模型去逼近超快速钟差预报中的非线性映射关系。随着预报历元的增加，偏离预报历元点越远的数据对模型精度的影响是逐渐减弱的，所以在实际钟差数据建模中，引入滑动窗的思想，在保持样本总数不变的情况，不断地用新的数据替换之前的已知数据作为KELM模型训练初始值。

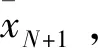
1)采用中位数粗差探测法[15]对超快速钟差进行数据预处理，剔除钟差序列中的粗差与钟跳等异常值。

2)将超快速钟差实测部分和预报部分进行分组，为了减小奇异样本对网络性能的影响，提高网络训练的速度，将数据集归一化到[0,1]之间。

3)设置相应的粒子规模、迭代次数等，对粒子的初始速度和初始位置进行随机化，初始化粒子对应核极限学习机的核参数与正则化系数，利用其训练KELM。

4)根据式(9)中的适应度函数，计算每个粒子的适应度值，不断更新个体极值和全局极值，根据式(6)和式(7)更新粒子的速度和位置，根据式(8)更新惯性系数。

5)判断每次迭代后的适应度值是否达到最优值或粒子的更新步数是否达到最大值，如果满足条件，参数优化过程终止，否则返回步骤4)。

6)将满足条件5)中对应的全局最优粒子解映射为KELM最优的核参数和正则化系数，代入式(5)与式(4)中，建立KELM超快速钟差预报模型，得到预报值，再将其进行反归一化处理，即得到最终预报值。

2 超快速钟差数据分析

iGMAS提供的超快速钟差包括观测部分(ISU-O)和预报部分(ISU-P)，各占24 h。ISU-O钟差通过对多个iGMAS分析中心解算的钟差进行综合加权所得，精度为1 ns；ISU-P钟差基于前一天的ISU-O钟差外推预报得到，并非某种单一预报模型的预报结果，精度为10 ns；最终精密钟差(ISC)通过事后处理得到，精度最高，为0.5 ns[16]。由于在获取超快速钟差与最终精密钟差的过程中，解算不同卫星钟差产品时各自所选用的参考钟不同，从而导致钟差改正中存在一定的系统性基准偏差。为了减少系统性基准偏差的影响，在对比ISU-P、ISU-O和ISC钟差之间的符合程度时，需要将各自的参考钟进行统一，一般选取钟差数据质量较高、序列连续性较好的卫星作为参考钟[17]，将其余卫星的钟差与参考钟的钟差作差，消除系统性基准偏差的影响，再将三种卫星钟差的一次差分序列对应作差，就得到ISU-P、ISU-O和ISC钟差三者的二次差分值。

采用2018年6月28日的超快速钟差数据和6月29日的精密钟差数据，选择C01卫星作为参考钟，任选三颗不同型号的BDS卫星(不妨选取C03、C06、C14)进行绘图分析。图1给出了消除系统性基准偏差后的三颗卫星的ISU-P、ISU-O及ISC钟差的二次差分值图，其中O-P表示ISU-O与ISU-P钟差之间的符合程度，O-F表示ISU-O与ISC钟差之间的符合程度，P-F表示ISU-P与ISC钟差之间的符合程度，横坐标表示6 h的历元个数。

图1 三颗卫星的ISU-P、ISU-O及ISC钟差的差异Fig.1 Differences in ISU-P, ISU-O, and ISC clock differences for three satellites

为了定量地评定ISU-P、ISU-O及ISC钟差之间的差异，可以采用二次差序列对应的均方根(RMS)值来表示三种类型卫星钟差之间的符合程度，统计平均精度结果如表1所示。

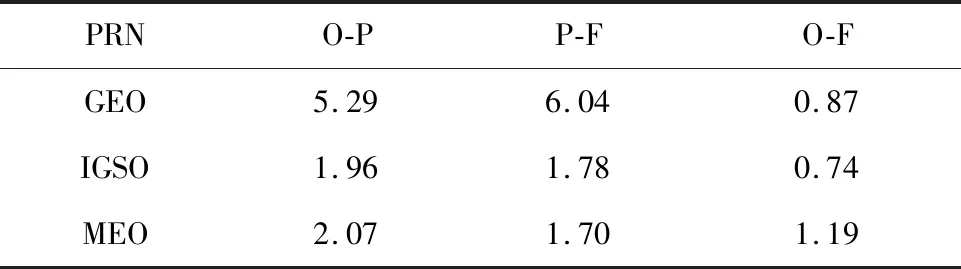
表1 不同类型的BDS卫星的ISU-P、ISU-O及ISC钟差二次差精度统计Table 1 ISU-P, ISU-O and ISC clock difference accuracy statistics of different types of BDS satellites ns

从图1和表1的结果可以看出：采用二次差法消除系统性基准偏差后，三颗卫星的O-F趋势一致，不同类型卫星的O-F的RMS值均接近亚纳秒级，而O-P、P-F的RMS值都比较大，说明超快速钟差预报部分(ISU-P)精度较低。说明ISU-P钟差与ISC钟差之间的符合程度最差，ISU-O钟差与ISC钟差之间的符合程度最好。

3 算例分析

由上述分析可以发现，iGMAS提供的ISU-P钟差精度较低，每6h更新一次。本文选取了iGMAS发布的BDS超快速钟差产品，数据采集时间为2018年6月19至6月29日(MJD 58288-58298)，选用了BDS不同型号的卫星(C01-C14)进行超快速钟差预报。

首先，进行数据预处理，统计该时间段内十四颗BDS卫星的ISU-P钟差精度；然后，使用24 h的ISU-O钟差数据，分别采用二次多项式(Quadratic polynomial，QP)、二次多项式结合周期项(Quadratic polynomial additional period，QP-Period) 及基于粒子群优化核极限学习机(PSO-KELM)模型进行6 h的短期钟差预报，并且使用ISU-O钟差进行精度验证。卫星在解算轨道和钟差的过程中，会受到轨道周期和外界环境的干扰，轨道误差和钟差会产生相互耦合的现象，导致卫星钟差结果存在着周期变化，因此，一些学者在卫星钟差预报中加入周期项改正，对BDS三种类型的卫星钟预报模型中各增加两个主显著周期项，其中GEO和IGSO卫星的主显著周期项为12 h和24 h，MEO卫星的主显著周期项为6 h和12 h[18-19]。

3.1 单天预报算例

首先，选取超快速钟差训练样本，粒子群算法初始化时，经过多次试验，设定粒子群规模为40，惯性系数范围为[0.5,1.0]，学习因子均为2，算法终止条件为收敛精度达到1×10-12或迭代次数达到800；然后，利用PSO算法选择合适的核参数和正则化系数后，代入式(5)和式(4)中，建立KELM超快速钟差预报模型进行钟差预报；最后，再将预报结果进行反归一化得到超快速钟差预报值。采用2018年6月26日的BDS超快速钟差数据进行6 h短期钟差预报，图2给出了ISU-P钟差和采用其他三种不同模型进行预报的预报残差图，横坐标表示预报6 h的历元个数，表2给出了ISU-P钟差和其他三种不同模型预报结果的精度统计，以及PSO-KELM模型预报值相对于ISU-P钟差与QP模型预报值两者的改进率。

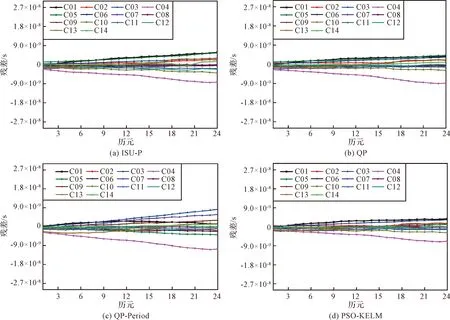
图2 不同预报模型下BDS卫星超快速钟差预报残差序列Fig.2 Super-fast clock offset prediction residual sequence of BDS satellite under different predicting models

从图2和表2可以看出：

1)有十颗卫星的ISU-P钟差精度与采用QP模型的预报精度大致接近，但是当采用QP-Period模型进行预报时，仅有三颗卫星(C01、C05、C10)的预报精度较ISU-P钟差和QP模型预报结果有所提升，这也说明了在超快速钟差预报模型中直接加入传统经验所得的主显著周期项后，预报精度不一定会得到提高。

2)通过图2中C04卫星的预报残差曲线对比可看出，采用PSO-KELM模型对该卫星进行预报的精度，相较于其他三种模型有了很大改进，预报残差的发散程度显著减小，且C04卫星预报精度达到0.65 ns，提高非常显著。

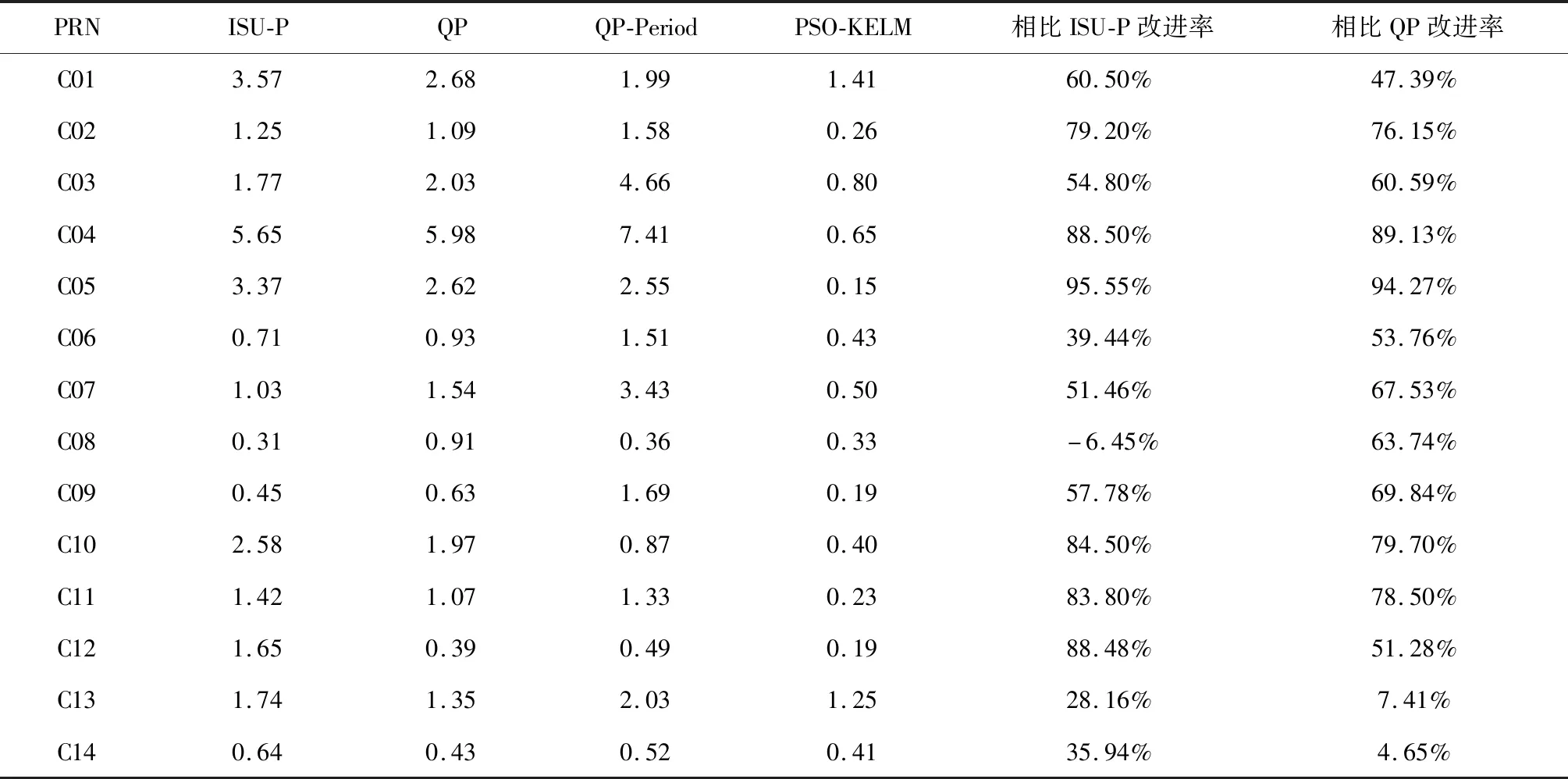
表2 BDS超快速钟差预报6 h结果单天精度统计Table 2 BDS ultra-rapid clock offset forecast 6 h results single-day accuracy statistics ns

3)采用PSO-KELM模型进行超快速钟差预报时，有十二颗卫星的RMS值都能达到亚纳秒级，说明该预报模型较好地表示了钟差时间序列的非线性特性。

3.2 多天预报算例

为了更好地说明本文方法的普适性，采用了2018年6月19至6月29日共十一天的BDS超快速钟差数据进行6 h短期钟差预报，表3给出了ISU-P钟差和采用其他三种不同模型进行预报的多天平均精度统计，以及PSO-KELM模型预报值相对于ISU-P钟差和QP模型预报值两者的改进率。

表3 BDS卫星超快速钟差预报6 h结果多天平均精度统计Table 3 BDS satellite ultra-rapid clock offset forecast 6 h results multi-day average accuracy statistics ns

由表3可以看出：

1)ISU-P钟差的精度普遍较低，有十二颗卫星的ISU-P钟差精度大于3 ns，这是因为ISU-P钟差的预报模型仅为简单的QP或QP-Period模型，经过我国十三家分析中心的预报产品加权得到再进行发布。

2)在本次实验使用的十四颗BDS卫星中，采用PSO-KELM模型较ISU-P钟差、QP模型及QP-Period模型的预报精度均有很大提高。以C07卫星为例，其多天的ISU-P钟差的平均精度在十四颗卫星中是较低的，为4.49 ns，采用QP和QP-Period模型对该卫星进行预报的多天平均精度分别为4.28 ns和4.58 ns，当采用PSO-KELM模型进行预报时，该卫星的多天平均精度为1.62 ns，较前三种预报模型的提升幅度均达到60%以上，提高较为显著。

为了更好地研究超快速钟差预报效果与卫星原子钟轨道类型的关系，表4统计了不同轨道类型的BDS卫星超快速钟差预报多天的平均精度。

表4 不同类型的BDS卫星超快速钟差预报多天平均精度统计Table 4 Multi-day average accuracy statistics of different types of BDS satellites for ultra-rapid clock offset predictionns

由表4的平均精度统计可以发现：

1)GEO卫星的ISU-P钟差精度和采用另外三种模型预报的精度都是最低的，出现这种结果的主要原因与卫星轨道的类型及卫星的发射时间有关，其中GEO卫星的发射时间较早。

2)当采用QP-Period模型进行6h的短期预报时，GEO卫星和IGSO卫星都较QP模型预报精度有所提高，但MEO卫星的预报效果相反，其采用QP-Period模型的预报精度下降，这也说明了GEO卫星和IGSO卫星的周期特性相比于MEO卫星较为显著，在MEO卫星的QP模型中加入周期项后反而造成了过拟合，使QP-Period模型对MEO卫星的预报精度降低。

3)对于不同类型的BDS卫星进行预报，采用本文所构建的PSO-KELM模型进行超快速钟差预报的精度均优于ISU-P钟差、QP模型及QP-Period模型的预报结果，并且本文方法对GEO卫星超快速钟差预报精度的改进率最大。

3.3 PSO-KELM预报值与ISC钟差符合程度分析

为了进一步地验证采用PSO-KELM模型进行BDS超快速钟差预报的可靠性，采用第2节中相同处理方法消除系统性基准偏差的影响(参考钟同样选取C01卫星)，评定PSO-KELM预报值与ISU-O及ISC钟差的符合程度。图3给出了与第2节中相同时间内的三颗不同型号卫星(分别为C03、C06、C14)的PSO-KELM预报值、ISU-O及ISC钟差的二次差分值图像，其中O-P′表示ISU-O钟差与PSO-KELM预报值之间的符合程度，O-F表示ISU-O与ISC钟差之间的符合程度，P′-F表示PSO-KELM预报值与ISC钟差之间的符合程度。

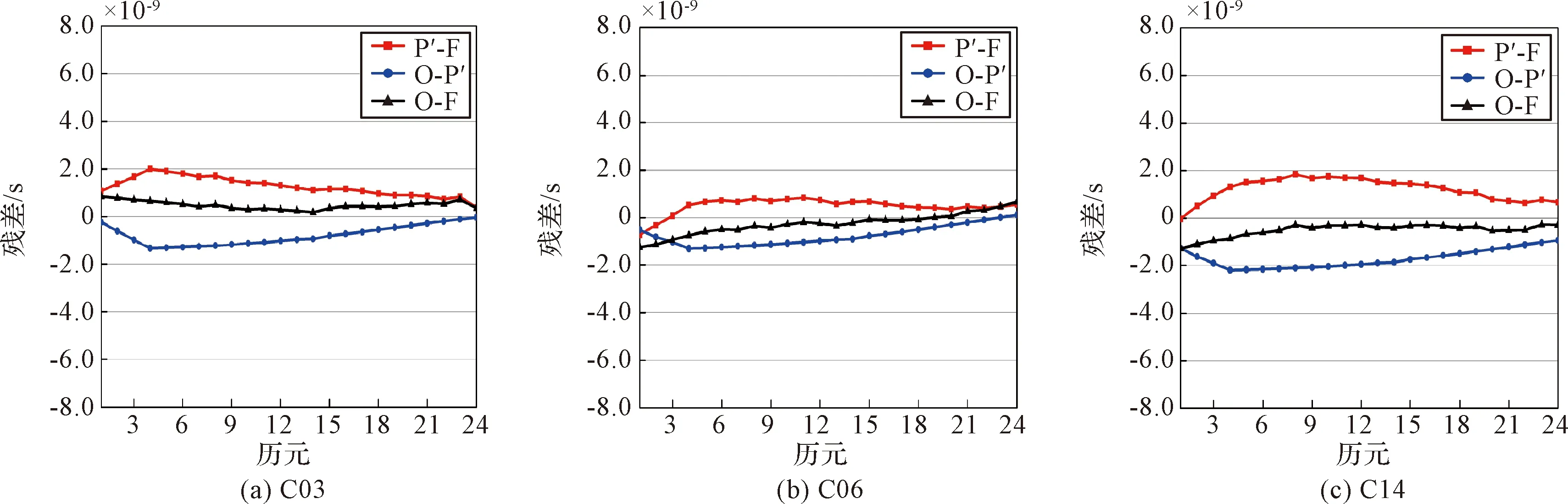
图3 三颗卫星的PSO-KELM预报值、ISU-O及ISC钟差的差异Fig.3 Differences in PSO-KELM prediction values, ISU-O and ISC clock differences for three satellites

通过比较图1和图3可以发现，选取相同的参考钟策略，消除了不同卫星钟差产品间的系统性基准偏差后，采用本文方法预报得到的BDS超快速钟差产品与ISU-O、ISC钟差之间的差异明显变小，并且卫星钟差的二次差分值图像明显收敛了许多。这说明相比于iGMAS提供的超快速钟差预报产品，采用本文模型进行超快速钟差短期预报的精度有了很大的提高，PSO-KELM预报值与ISC钟差之间的符合程度显著增强。

表5 不同类型的BDS卫星的PSO-KELM预报值、ISU-O及ISC钟差二次差精度统计Table 5 PSO-KELM prediction values, ISU-O and ISC clock difference accuracy statistics of different types of BDS satellites ns

比较表1和表5的结果可以看出，对于不同类型的BDS卫星而言，消除了不同卫星钟差产品间的系统性基准偏差后，采用本文模型进行超快速钟差短期预报的PSO-KELM预报值与iGMAS提供的超快速钟差预报产品相比，GEO、IGSO和MEO卫星超快速钟差预报部分与最终精密钟差的二次差精度分别提高了1.89 ns，0.68 ns和0.29 ns，这就说明了采用本文模型可以很好地提高BDS超快速钟差预报部分的精度，也间接检验了采用本文建立的方法进行BDS超快速钟差短期预报的有效性。

4 结 论

通过利用我国iGMAS提供的单天和多天BDS超快速钟差数据，进行6h的短期预报实验，有以下结论：

1)核参数与正则化系数的合理选择，影响着KELM超快速钟差预报模型的正确性，引入PSO算法避免了人为选择KELM参数的盲目性，能够较好地解决KELM算法的核参数及正则化系数的选择问题，提高了超快速钟差短期预报的精度。

2)采用本文PSO-KELM模型得到的BDS超快速钟差预报产品精度相比于QP和QP-Period模型精度有较大提升，相比与iGMAS超快速钟差预报产品，GEO、IGSO和MEO卫星分别提升了50.51%,46.98%,40.67%。

3)消除不同钟差产品之间的系统性基准偏差后，PSO-KELM超快速钟差预报值与最终精密钟差的符合程度显著增强，说明PSO-KELM预报模型可以应用于北斗超快速钟差的高精度预报。