UKF参数估计在航天器气动辅助变轨问题中的应用
本立言,谢祥华,张 锐
(上海微小卫星工程中心,上海 201203)
0 引 言
London[1]首次提出气动辅助变轨方式,这对于航天器轨道转移任务而言,可以节约大量的燃料,吸引了众多学者的研究。气动辅助变轨是指具有一定形状的航天器经过大气层,通过调整升力系数以及阻力系数,来降低航天器能量或者改变轨道平面。在气动辅助变轨问题中,主要热点集中于航天器在大气层内的飞行控制,Miele等[2]研究了航天器在大气层中的飞行规律,给出了9种轨道转移最优控制指标,其中比较重要的有燃料最省指标和时间最短指标。
在气动辅助变轨问题中,传统数值方法可分为直接法和间接法。直接法通过不同的离散化方法对控制量进行参数化,把原优化问题转化为带有约束的参数优化问题,然后采用非线性规划算法进行求解。这类方法目前的研究热点是伪谱法[3-6],该方法虽然具有求解精度较高、寻优参数少、收敛性好的优点,但仍然需要猜测初值,严重依赖非线性规划算法的求解能力。对于气动辅助变轨问题,控制律较为震荡[7],数值经验表明,伪谱法在求解此类问题时效率以及计算精度都出现明显的降低[8],由于伪谱法很难捕获到控制跳跃点,会出现虚拟数值振荡[9-10]。为得到精确的控制律,常用的改进算法有hp自适应伪谱法[11-13],通过划分网格和增加配点个数,来控制参数优化问题规模和提高逼近精度,但失去了全局快速收敛优势。
间接法首先根据极大值原理将最优控制问题转化为两点边值问题[14],然后利用各种数值方法求解[15-17],常用的有打靶法。尽管采用间接法可以得到精确的最优控制律,但这种方法求解过程比较复杂,需要获取目标函数或者终值误差函数对于状态变量以及协态变量的梯度矩阵,而且对初值非常敏感,由于协态变量没有明确的物理含义,因此初值难以猜测,收敛范围小,给求解问题带来了很大的困难。
针对上述研究现状,本文提出一种基于无损卡尔曼滤波(UKF) 参数估计的气动辅助变轨问题求解方法,首先将气动辅助变轨所对应的两点边值问题转化为参数估计问题,然后用UKF滤波器进行参数估计,从而得到精确解。由于UKF滤波算法基于估计理论,不依赖梯度信息,避免梯度矩阵的推导,而且克服了猜测协态变量初值的困难,降低了求解气动辅助变轨问题的难度。数值仿真结果表明,该方法求解效率高,具有良好的鲁棒性,可以很好的解决气动辅助变轨问题。
1 过程描述
气动辅助轨道变轨过程如图1所示。在初始轨道施加一个反向的速度增量ΔV1后,航天器进入转移轨道,该轨道的远地点为变轨点1,航天器于特征点2进入大气层后,在大气层内通过调整升力系数,在特征点3飞出大气层,进入转移轨道,该轨道的远地点为特征点4,在特征点4施加速度增量ΔV2,使航天器进入目标轨道,从而完成气动辅助轨道转移。记μ为地球引力常数,r1和r2分别为初始轨道和目标轨道的地心距,ra为大气层边界地心距。
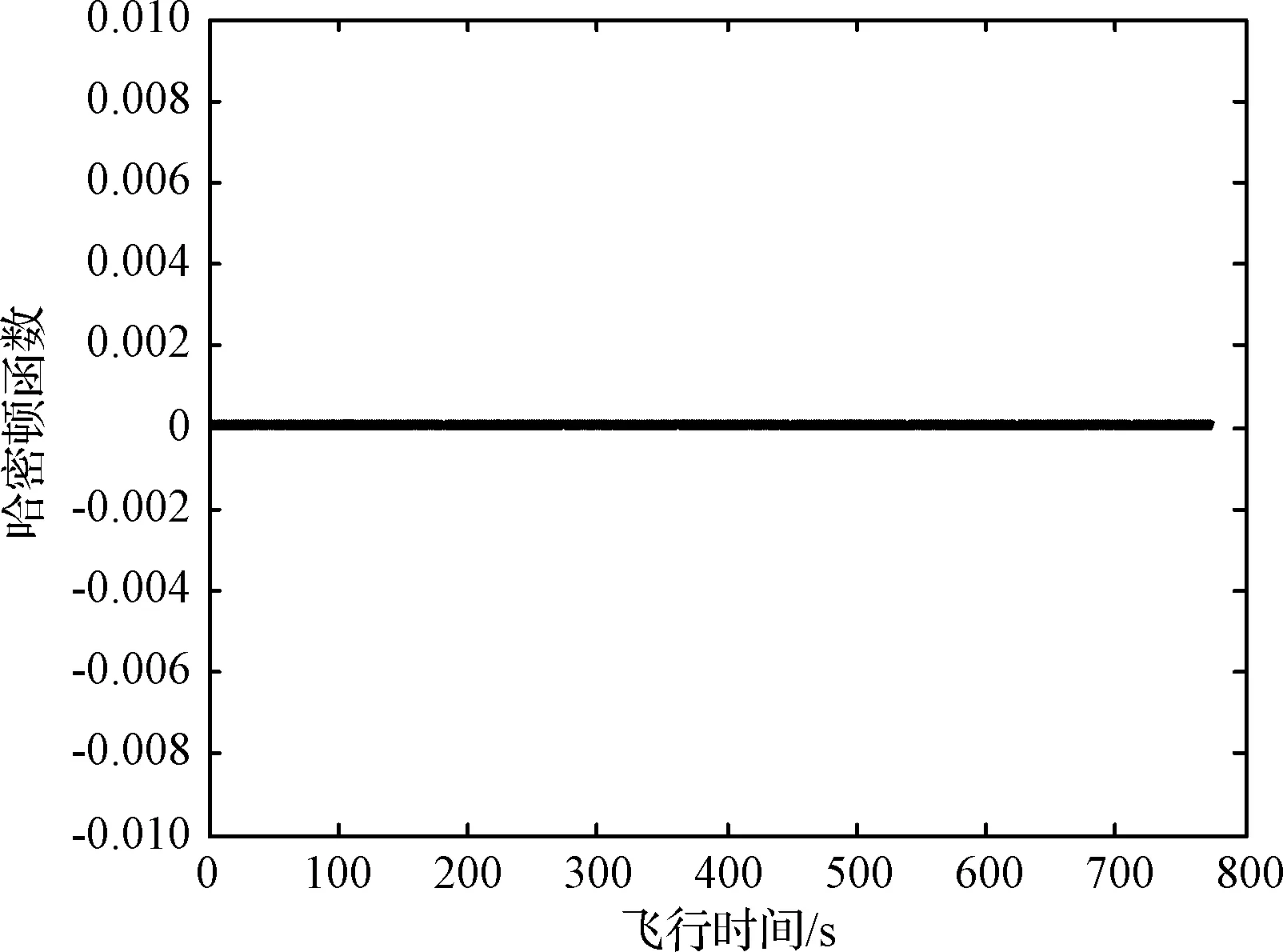
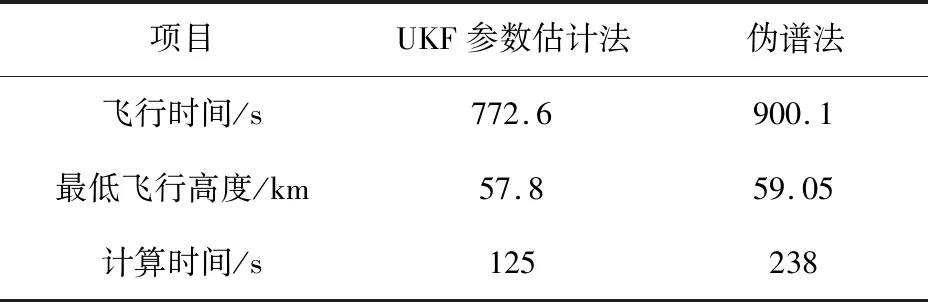
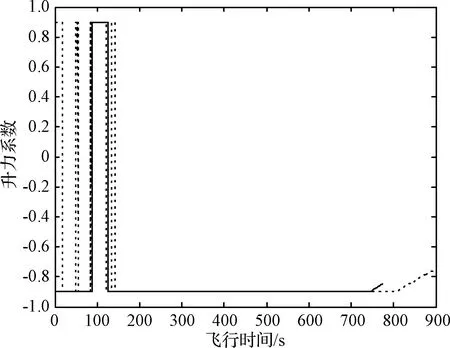
为了获取足够气动力,航天器必须进入大气层,即转移轨道近地点必须确保在大气层内,令近地点地心距为rpe,则rpe (1) 由于rpe值对优化结果并不敏感,在本文算例中,若rpe相差50 km,则ΔV1仅改变9 m/s,因此可认为固定不变。记大气入口点的地心距r0,速度V0以及航迹角γ0分别满足 r0=ra (2) (3) (4) 根据切入点约束条件,保证转移轨道远地点高度为r2,根据动量守恒以及能量守恒定律,则大气出口点的地心距rf、速度Vf和航迹角γf满足 rf=ra (5) (6) 特征点4变轨前后速度分别为 (7) (8) 则第二次施加速度增量 (9) 速度增量ΔV2的大小与大气出口点的航迹角极为敏感,当γf=0°,ΔV2最优,为了确保航天器能顺利飞出大气层,则需要稍大于0°,因此认为γf为一稍大于0°的固定值,所以,在航天器气动辅助轨道转移的过程中,主要优化过程集中于大气飞行段,在满足入口r0,V0,r0出口rf,Vf,γf条件下,通过调整升力系数,使航天器尽快从大气层中逃逸,避免气动加热时间过长,因此将转移时间最优作为性能指标。 假设航天器在大气内飞行仅受气动力和地心引力作用,则平面内运动方程为 (10) 式中:r,V,γ以及m分别表示航天器的地心距、速度、航迹角以及质量,D和L分别表示气动阻力以及气动升力,其表达式分别为 (11) 式中:S为气动参考面积,ρ为大气密度,定义ρ0为海平面大气密度,β为指数因子,h为航天器地心高度,则ρ表达式为 ρ=ρ0exp(-βh) (12) (13) 式中:CD0和K分别表示零升阻力系数和诱导阻力因子。 则转移时间最优问题性能指标可以记为 (14) 记状态变量x=[r,V,γ]T,协态变量λ=[λr,λV,λγ]T,则哈密顿函数H为: (15) 状态与协态方程: (16) 初始条件: (17) 末端条件: (18) 哈密顿函数H的末值约束: H(tf)=0 (19) (20) 则最优控制律如下所示: 若λV<0,则 (21) 式中:CLS具体表达式为 (22) 若λγ≥0,则 (23) 本节将求解最优控制的两点边值问题改写为参数估计问题,如果选择估计参数为初始协态变量λ(t0)=[λr(t0),λV(t0),λγ(t0)]T以及转移时间tf,则输出末端约束条件有:r(tf),V(tf),γ(tf)以及H(tf),若初始估计参数不当,则出现碰撞地球的情况,速度接近为 0 m·s-1,导致积分无法进行,为了避免上述情况,将积分停止条件设置为当前速度到达目标速度Vf,则上述问题可以降低一维,避免对转移时间的猜测,减少求解问题的难度,则估计参数wk与期望输出dk分别为 wk=[λrk(t0),λVk(t0),λγk(t0)]T (24) dk=[rk(tf),γk(tf),Hk(tf)]T (25) 记xk为初始状态变量,则dk是xk和wk的函数,可通过以xk和wk为初始条件,积分方程(16)求解,记这个函数为 dk=G(xk,wk) (26) 将上述参数估计问题写成状态空间表达式: (27) 式(27)表示了一个状态转移矩阵为单位阵的静态过程,rk为过程噪声,期望输出dk则与wk满足确定的非线性关系,ek为观测噪声。 则该参数估计问题就可以用各种滤波算法求解,这里直接给出基于UKF滤波器的参数估计算法流程,如图2所示,其中: (28) 式中:N是w的维数,η是尺度参数,ε决定了无损变换的σ点相对于w当前均值的分布范围,一般设为小量,取值范围为[10-4,1]。常量κ一般取为0或3-N,β是与w先验分布的相关常量,对于高斯分布,β=2是最优的,ρRLS为遗忘因子,用于防止因模型误差较大造成的滤波发散,其取值范围为(0,1]。 滤波参数对滤波收敛的过程影响很大,如选取不合适,会导致滤波收敛过程的振荡幅度很大,不能较快收敛,甚至发散。本文通过大量数值仿真,给出了可调参数的推荐值,如表1所示,其中尺度参数ε随着滤波进行,该值随观测误差的减小而减小,有利于算法的快速收敛。 表1 滤波器参数Table 1 The value of UKF parameter estimation 图2 UKF参数估计流程图Fig.2 The flow chart of UKF parameter estimation 本节给出了一个利用UKF参数估计算法求解气动辅助平面变轨的算例,算例中参数的具体数值见表2。为了增强算法求解效率,将各物理量进行归一化处理,其中,长度量纲选取106m,时间量纲选取103s。积分方法选择取四阶龙格库塔方法,积分步长为0.5 s。 图4 控制量变化曲线Fig.4 Optimal control vs time 图5 哈密顿函数变化曲线Fig.5 Hamilton function vs time 对比文献[3,7]的结果,两者状态变化趋势是一致的,则验证了该算法的正确性。图5中哈密顿函数值在整个飞行过程中近似保持不变,则验证了所得结果的最优性。航天器飞出大气层外在r2处速度为7495.7 m·s-1,航迹角为0.4°,则整个转移过程中需要特征速度增量为霍曼转移所需特征速度增量的49.9%,接近理想的49.3%。 为了研究UKF参数估计法的求解性能,将计算结果与hp自适应Radau伪谱法(简称伪谱法)的计算结果作比较,具体结果见表3。 表3 优化结果的对比Table 3 Comparation of the optimal result 图6给出了两种算法得到的控制律,其中,实线为UKF参数估计法的计算结果,虚线为伪谱法的计算结果。比较升力系数变化,两种方法得到的控制律有一定差别,可以解释为两种方法得到不同的局部最优解,具体表现为性能指标的数值差别,伪谱法通过延长转移时间,抬高了航天器的最低飞行高度,降低了峰值热流。在实际工程应用中,为了使航天器在极端条件不被烧蚀,必须考虑热流的限制,保证航天器可靠性,可以作为下一步研究工作。从图6可以看出,UKF参数估计法得到的控制律过度光滑,精度高,没有出现虚拟数值震荡。 在相同计算条件下(Intel G870 3.10 GHz),UKF参数估计法求解效率优于伪谱法,而且利用UKF参数估计法,算法结构简单,不需要强大的非线性规划软件包。 图6 最优控制律的对比Fig.6 Comparation of the optimal control 本文提出了一种基于UKF参数估计的气动辅助变轨求解算法。该方法克服猜测协态变量初值的困难,协态变量初值可以随机选取,同时避免了打靶法对梯度矩阵的推导,因此降低了求解气动辅助变轨问题的难度。数值仿真表明:该方法结构简单,求解效率高,具有良好的鲁棒性,可以作为求解气动辅助变轨的一个有力工具。2 优化模型
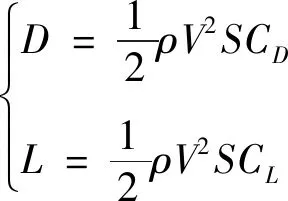

3 利用UKF参数估计求解气动辅助平面变轨问题

4 算例与分析
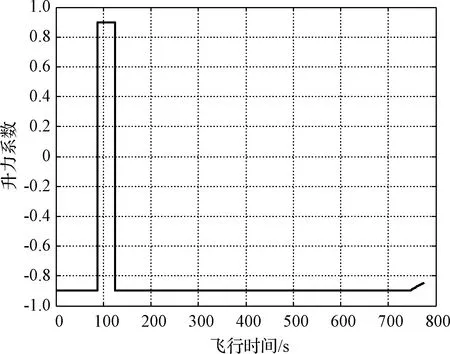
5 结 论

