火星大气进入段纵向可达区生成的解析同伦法

赵泽端，崔平远，朱圣英

(1. 北京理工大学宇航学院，北京 100081；2. 深空自主导航与控制工信部重点实验室，北京 100081；3.飞行器动力学与控制教育部重点实验室，北京 100081)

0 引 言

目前的火星着陆任务从进入到最后着陆过程均采用与1976年海盗号(Viking)任务类似的着陆框架，着陆阶段分为大气进入段、伞降段、动力下降段和着陆段[1]。火星大气进入段指的是探测器从进入火星大气(距离火星表面约125 km)到降落伞展开的飞行阶段。在进入段，探测器需利用火星大气消耗掉自身的绝大部分能量，将速度从进入点约6 km/s减到开伞点约500 m/s，高度从进入点约125 km 降至开伞点约10 km左右[2-3]。

可达区指探测器在同一初始状态及任务参数约束下的所有可达终端状态，与可控集一样反应了探测器的飞行能力[4-6]。可达区分析对于任务设计、着陆点选取及风险评估等均具有重要意义[7-8]。针对中高升阻比飞行器，Lu等[9]基于准平衡滑翔假设及简化的动力学方程，提出一种解析可达区求解方法，该方法可最终将可达区求解转换成区间范围已知的单参数寻优问题，保证了求解的效率和可靠性。但准平衡滑翔假设不适用于目前火星任务采用的小升阻比飞行器[10]。针对小升阻比飞行器，Saraf等[11]提出根据满足路径约束的最大最小阻力加速度剖面来得到最小最大航程，并通过对最大最小阻力加速度插值的方式得到介于最小最大航程之间的轨迹。该方法可以得到一个保守的可达区，是探测器实际可达区内的子集。与此类似，Li等[12]通过将过程约束描述在r-V平面内，可以快速获得飞行器的可达区内边界(靠近初始位置)。Benito等[4]通过将可能的可达区域划分成网格，对每一个网格点利用直接优化方法检测其可行性，最终得到可达区及每一个可达点对应的最大开伞高度。该方法需要对每一个网格点单独求取最优化问题，计算量大，求解过程的收敛性及可靠性难以保证。Helsen等[13]通过假设一个比实际可达区更大的边界，并利用直接优化方法单独求取离每一个边界点最近的点，这些点组成飞行器的可达区。其思想与Lu等[9]采用的最优接近思想相同，求取方法与Benito等[4]的方法相似，属于直接优化方法。

直接法通过将状态和控制量离散，将原最优问题转换为非线性规划(NLP)问题，借助商业软件或工具箱求解，具有通用性高、问题建模相对容易的特点。但直接法的求解依赖于初值猜测，当初值猜测不理想时，求解过程可能会陷入局部最优解，不满足最优必要条件，也可能不收敛。间接法的理论基础是庞特里亚金极小值原理，通过将原优化问题转换为一个等价的两点边值问题求解，对最优必要条件的满足较好。但由于协状态缺乏物理意义，且问题对协状态初值比较敏感，故间接法存在协态初值猜测困难的问题。

对于可以横纵向解耦的小升阻比火星进入探测器，基于其纵向动力学方程的最优控制问题一般均属于bang-bang控制，初值收敛域小且对初值敏感。Bertrand等[14]针对bang-bang最优控制问题，应用同伦法分析不同的初始辅助优化问题对于解的收敛性和求解速度的影响。同伦法在求解小推力星际转移轨道最优问题方面已经有了深入的研究[15]。在火星大气进入制导方面，Zheng等[16]利用同伦法求解了最大开伞高度问题。

本文利用解析同伦法思想，在纵向动力学背景下，考虑数值延拓的效率和可靠性，首先为无路径约束的最大/最小开伞高度、最大/最小航程问题分别创建合适的辅助优化问题。并从最大/最小开伞点高度问题出发，延拓出纵向可达区。由于利用解析同伦法思想，从已知最优解的最优辅助问题出发延拓到所关心的最优问题，避免了初值猜测困难的问题；通过四个基本的最优问题延拓出纵向可达区，避免了对可达区内部点可行性的验证。

1 火星大气进入段动力学模型

由于火星大气进入段持续时间较短，可以忽略火星自转的影响，在火星固连系下建立三自由度动力学模型如下

(1)

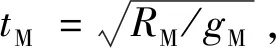
(2)

式中：ρ为大气密度，CD为阻力系数，Sref为防热底的参考面积，m为探测器质量。此处需强调的是，除系统状态变量外，其他变量若未特别说明外均未做无量纲化处理。

由于目前的探测器在火星大气进入过程中均采用平衡攻角，为简化分析过程，可近似将升阻比当成常数，故可得到无量纲的升力加速度为

L=D(L/D)

(3)

式中：L/D为升阻比。在本文的研究中，火星大气密度模型采用如下的指数模型

ρ=ρ0e-h/hs

(4)

式中：ρ0为参考大气密度，h为探测器当前高度，hs为参考高度。

由于目前所有火星着陆任务的探测器进入级均采用半锥角为70°的球锥形防热大底，该气动外型具有较小升阻比(升阻比小于0.3)，进入段攻角保持在平衡攻角附近，通过调整倾侧角的大小和方向来控制探测器的运动，故可在制导相关设计中将纵向和侧向解耦分析。建立纵向动力学模型如下

(5)

式中：s为运动轨迹长度在水平方向上的投影，即本文中的航程，用来近似替代水平位置。

考虑到火星大气进入段的扰动和不确定性，轨迹分析和设计时需留有足够的控制余量σ∈[σmin,σmax]，其中π>σmax>σmin>0。本文控制量取为倾侧角余弦u=cosσ，有如下的上下界约束

cosσmax≤u≤cosσmin

(6)

本文仅研究无路径约束下的最大/最小航程、最大/最小开伞高度及纵向可达区问题，有路径约束的相关问题可在本文的基础上，利用精确罚函数法和同伦法求解[14]。

2 路径自由的纵向可达区边界求解

本文所定义的纵向可达区主要是指同一初始条件下，探测器可以飞达的航程-高度范围。进入段的终端对应降落伞的展开条件，本文采取速度作为开伞触发条件，可达区分析时需满足的初始和终端条件如下

(7)

V(τf)=Vf

(8)

对于可达高度-航程剖面而言，其边界指的是最大/最小航程和最大/最小开伞高度。

2.1 最大/最小航程问题

2.1.1最大/最小航程原问题

最大航程对应探测器可飞达的最远距离，对应优化问题的性能指标为

Js,max=-s(τf)

(9)

最小航程对应探测器可飞达的最近距离，对应优化问题的性能指标为

Js,min=s(τf)

(10)

则路径自由的最大/最小航程问题可描述如下：

(11)

同时满足式(5)～式(8)。式(11)中，Js取-s(τf)或s(τf)时，分别对应最大航程问题Ps,max或最小航程问题Ps,min。

Hs=λTf

(12)

由欧拉-拉格朗日方程可得：

(13)

由横截条件及式(7)和式(8)可得：

(14)

由于终端时间自由且哈密顿函数中不显含时间，故

Hs(τ)≡0

(15)

由于控制变量u在哈密顿函数中是一阶形式，根据极小值原理，最优控制将是bang-bang的形式，切换条件为λγL/V，具体的切换过程为

(16)

由分析可知，λγL/V只可能在某些单点为零，故问题Ps并非严格意义上的奇异。从简化问题的角度考虑，可将λγL/V=0时的控制并入λγL/V>0的情况中。

综上，问题Ps可转换为如下的两点边值问题：

问题Ts：寻找由协状态初值和终端飞行时间组成的变量

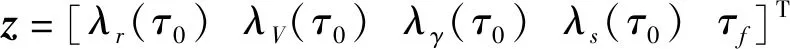
(17)

满足式(7)、(8)和(14)描述的边值条件，式(5)和(13)描述的微分方程条件，式(15)中的哈密顿函数条件及式(16)中的控制切换条件。

Ts,max和Ts,min分别对应最大/最小高度问题两点边值问题。由分析可知，问题Ts的控制为bang-bang形式，问题的求解将会对初值猜测特别敏感。由于协状态初值没有实际的物理意义，初值猜测比较困难。本文将构造最优解已知的辅助优化问题，通过解析同伦法求解该问题。

2.1.2最大/最小航程辅助优化问题

考虑到最大/最小航程问题的bang-bang最优控制特点，若辅助优化问题与原问题的最优解相差太远，则存在延拓失败的危险，即不能从辅助问题最优解最终得到原问题最优解。即使可以得到，也存在延拓过程过长，迭代计算量过大的缺点。故通过对原优化问题的初步分析得出更贴近原问题的辅助优化问题，可加快同伦迭代过程，相应减少计算量，并在一定程度上保证求解过程的稳定性。

对于火星大气进入段探测器，当控制量u取最大值，即倾侧角σ取最小值时，向上的升力将使得探测器在更高的高度飞行，飞行过程中较小的阻力将使得自身能量消耗速度更慢，探测器将能飞得更远，故取最大航程的辅助优化问题性能指标为

(18)

当探测器保持在最大倾侧角附近时，由于升力方向向下，探测器的高度降低较快，飞行过程中阻力较大，则其能量消耗得较快，飞得越近。故构造最小航程辅助优化问题性能指标为

(19)

最大/最小航程的辅助优化问题可统一表达为：

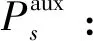
(20)

(21)

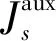
(22)

(23)

λV(τf)=0

(24)

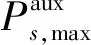
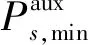
根据式(22)和式(24)的协状态终端值、式(13)的协状态微分方程以及正向积分得到的最优状态和飞行时间逆向积分即可得到辅助问题最优轨迹对应的协状态值及最优控制量。

2.1.3最大/最小航程问题同伦求解过程

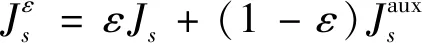
构建如下的优化问题：

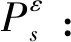
(25)

该问题的哈密顿函数为

(26)

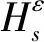
(27)

控制量u仍以一阶形式出现，故该问题的最优解仍是bang-bang形式。经分析可得，最优解具有如下的形式

(28)

其中，对λγL/V+ε-1=0情形的分析与问题Ps中的分析过程相似。下面不再赘述。

协状态的微分方程与问题Ps相同。横截条件如下：

(29)

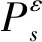
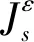
2.2 最大/最小开伞高度问题

2.2.1最大/最小开伞高度原问题

由于火星大气相对稀薄，在进入段探测器飞行高度较高，大气不能为其提供充足的减速能力。为了能为伞降段及后续的着陆段提供足够的时间和空间，同时也为了能探测火星南极海拔更高的古大陆，提高探测器进入段末端的开伞高度一直是进入段制导控制研究的重点。对于最大开伞高度问题，取性能指标如下

Jh,max=-r(τf)

(30)

实际工程设计中，可能的最低开伞高度影响着后续故障预案的设计，以及标称航程在可达区内的选择，具有十分重要的意义。对于最小开伞高度问题，取性能指标如下

Jh,min=r(τf)

(31)

则路径自由的最大/最小化开伞高度优化问题可描述如下

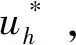
(32)

同时满足：式(5)～式(8)。式(32)中，Jh取-r(τf)或r(τf)时分别对应最大高度问题Ph,max或最小开伞高度问题Ph,min。

(33)

问题Ph的求解可转换为求解两点边值问题Th：寻找由协状态初值和终端飞行时间组成的变量z，满足式(7)、(8)和(33)描述的边值条件，式(5)和(13)描述的微分方程条件，式(15)中的哈密顿函数条件及式(16)中的控制切换条件。

2.2.2最大/最小开伞高度辅助优化问题

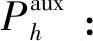
(34)

同时满足式(5)～式(8)。

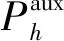
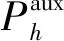
2.2.3最大/最小开伞高度问题同伦求解过程

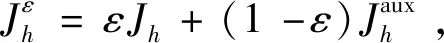
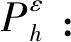
(35)

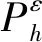
(36)

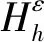
(37)

由于积分项中不显含状态变量，故该问题的协状态微分方程与问题Ps相同，横截条件为

(38)

由于式(36)中，控制量u以二阶的形式出现，由二次函数在u∈[umin,umax]的最小值分析可知，该问题的最优控制结构如下

(39)

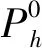
3 纵向可达区求解

为了从第2节的子优化问题得到纵向可达区，取性能指标为Jsk，构建如下优化模型。

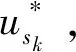
(40)

同时满足式(5)～式(8)以及式(41)

s(τf)=sk

(41)

当Jsk=-r(τf)时，对应求解可达航程及其最大高度边界；当Jsk=r(τf)对应求解可达航程范围及最低高度边界。

相比于问题Ph，问题RA多了一个终端航程约束。问题RA的哈密顿函数与问题Ph相同，且对于时间保持恒为零值，故二者的协状态微分方程相同。问题RA的横截条件为

(42)

构造两个单调航程序列：{s0,…,si,si+1,…,sI}与{s0,…,sj,sj+1,…,sJ}，满足s0为问题Ph对应的航程，sI为问题Ps,min对应的航程，sJ为问题Ps,max对应的航程，分别从问题Ph的最优解出发，按照序列依次求解问题RA，其中第k次的最优解zk作为第k+1次问题求解初值，最终可得到纵向可达区。

4 仿真校验

本节探测器的物理参数、初始条件及开伞条件部分根据文献[15]选取。其中质量m为2800 kg，参考面积Sref为15.9 m2，升阻比L/D为0.24，阻力系数CD为1.45，初始条件及开伞条件具体如表1所示。

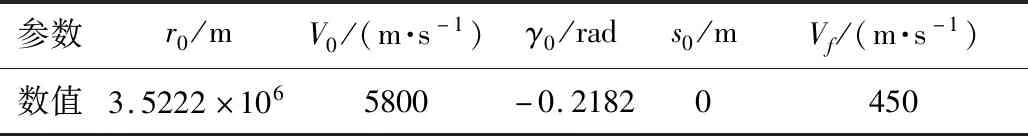
表1 探测器初始条件及开伞条件Table 1 Initial and terminal conditions of the vehicle

为了给制导控制系统留有控制余量，取最大倾侧角σmax为120°，最小倾侧角σmin为30°。在同伦延拓过程中，以下4个优化子问题的ε均从0开始，其中ε=0代表辅助优化问题的解。具体仿真结果如下。

4.1 最大航程问题

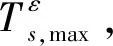
相比于σ≡σmin的进入轨迹，航程在ε由0变化到1时增加了约150 m，出现这种现象的主要原因在于飞行时间的增加，相比于ε由0.1变化到1的绝大部分过程，最大航程问题对应的末端航程仅增加了3 m，如图2所示。故在任务的快速分析设计中，可用σ≡σmin的进入轨迹近似代替最大航程轨迹来分析最大航程。

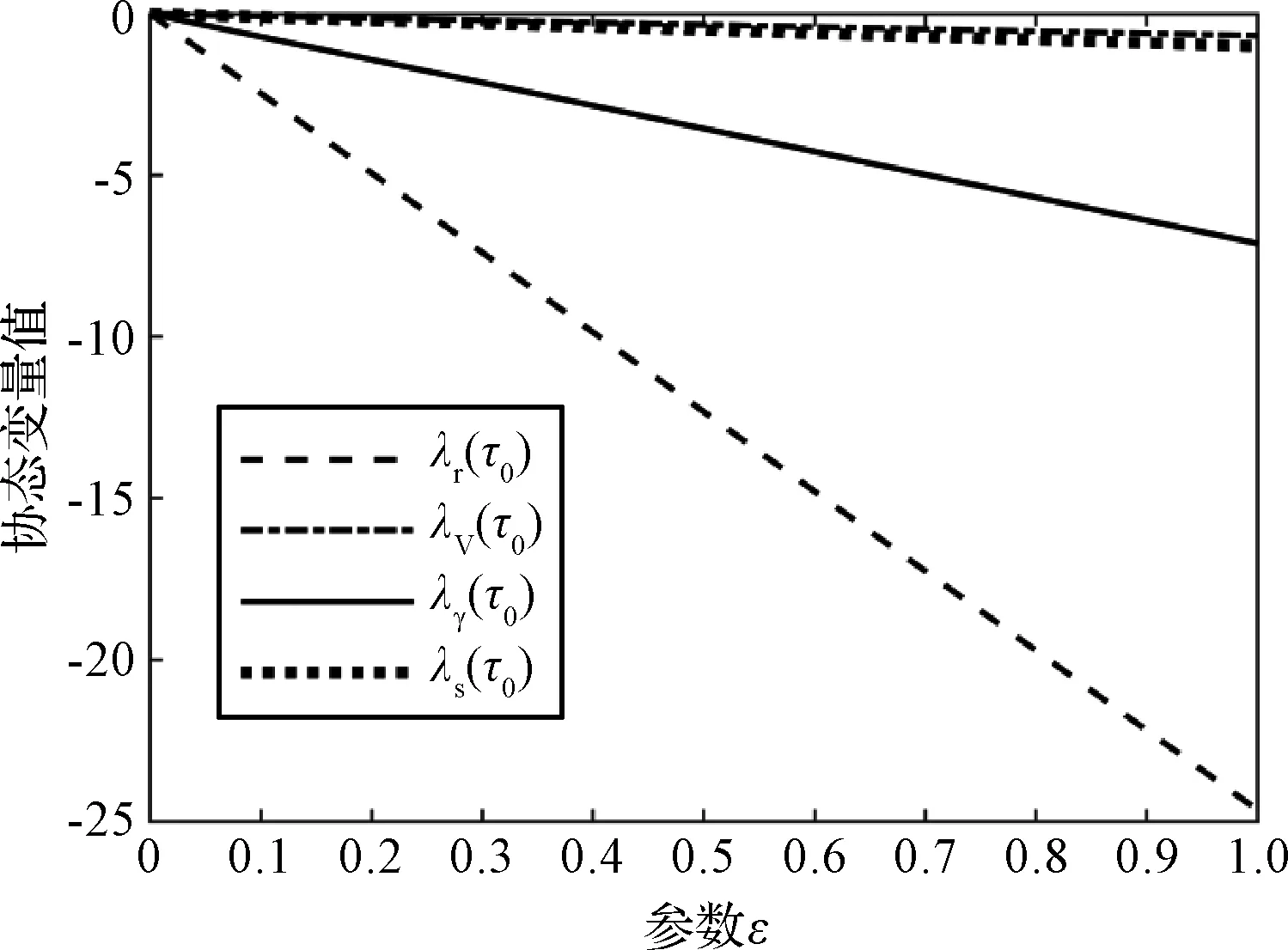
图1 问题中初始协状态值随参数ε的变化Fig.1 Variation of initialcostates with ε in

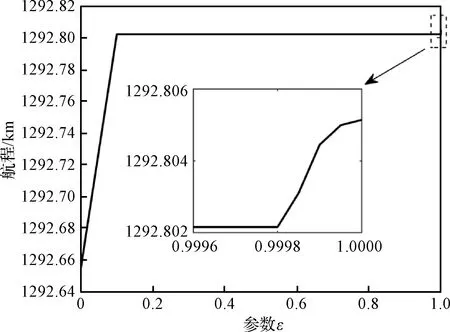
图2 问题中航程随参数ε的变化关系Fig.2 Variation of downrange withε in

4.2 最小航程问题

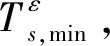
最小航程轨迹比倾侧角保持为σ≡σmax的进入轨迹末端航程高135 m，如图4所示，这种现象有可能是辅助问题求解时采取0.5 s步长，积分精度较低引起的。在任务的快速分析设计中，可用σ≡σmax的进入轨迹近似代替最小航程轨迹。

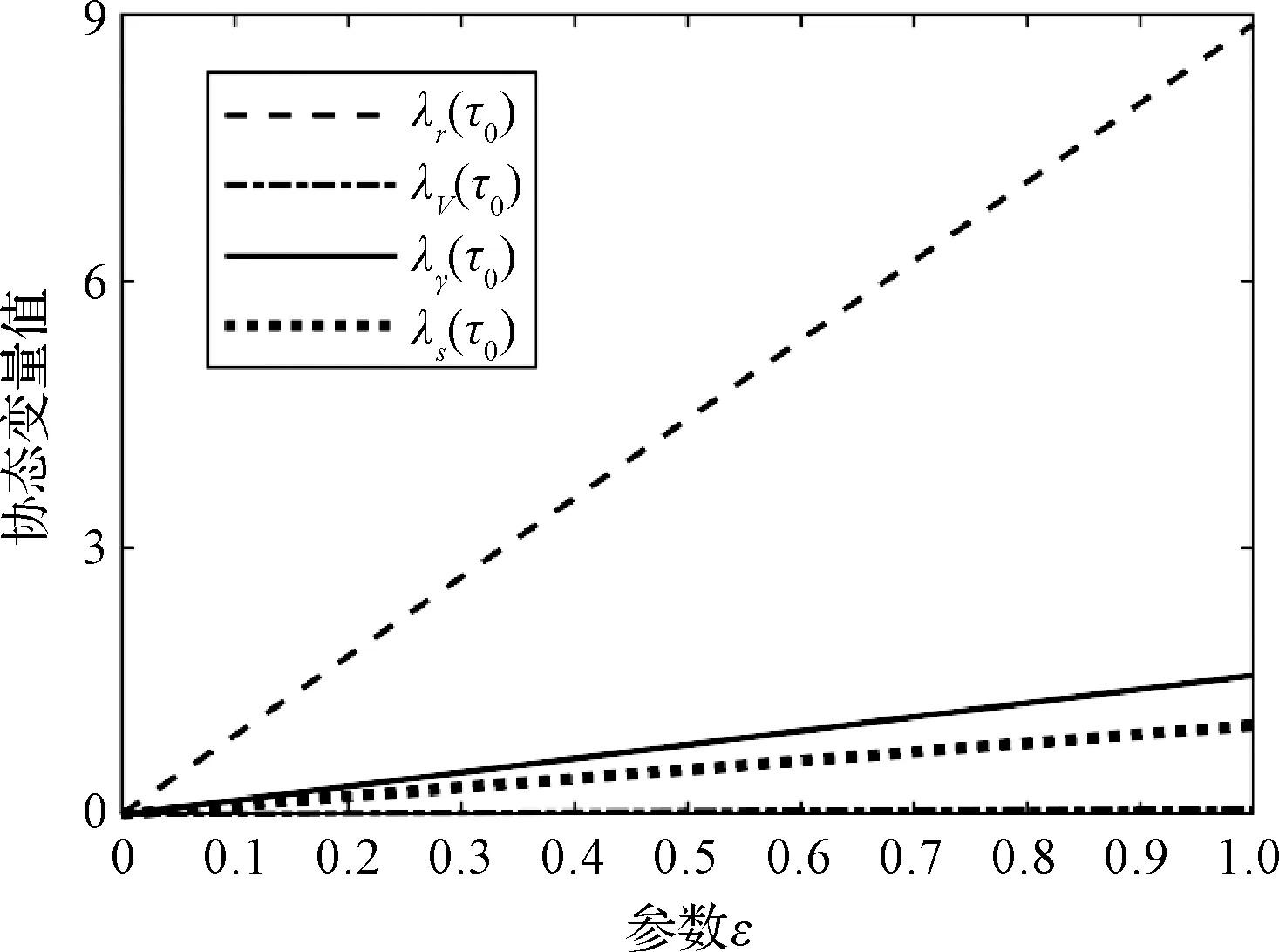
图3 问题中初始协状态值随参数ε的变化Fig.3 Variation of initialcostates with ε in

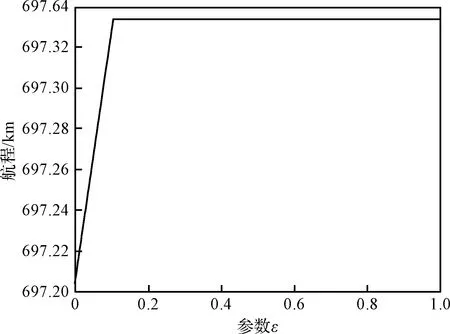
图4 问题中航程随参数ε的变化关系Fig.4 Variation of downrange with ε in

4.3 最大开伞高度问题

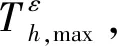
图5 问题中初始协状态值随参数ε的变化Fig.5 Variation of initialcostates with ε in

图6 问题中开伞高度随参数ε的变化关系Fig.6 Variation of terminal altitude with ε in

4.4 最小开伞高度问题

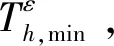
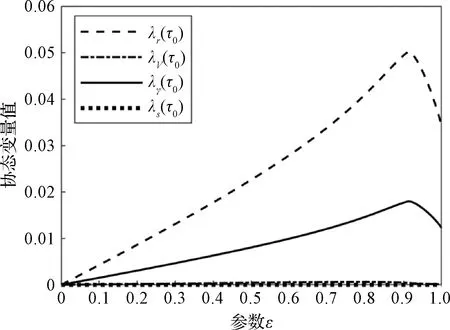
图7 问题中初始协状态值随参数ε的变化Fig.7 Variation of initialcostates with ε in

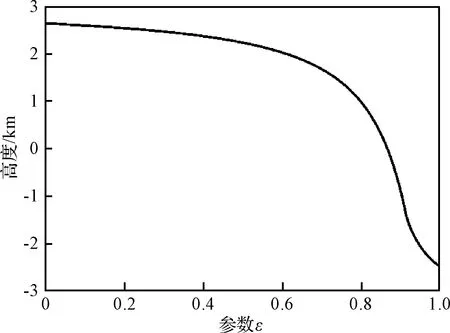
图8 问题中开伞高度随参数ε的变化关系Fig.8 Variation of terminal altitude with ε in

4.5 纵向可达区

另外选取两个不同的初始航迹角：γ0=-14°和γ0=-13°。在分别求取4个子优化问题的基础上分别求解问题RA。其中γ0=-14°和γ0=-13°的子问题既可以分别从辅助优化问题出发求解，也可以从γ0=-12.5°的4个子问题最优解出发，构造{γk1,γk2,…,γkN}的序列，采用同伦法求解，其中γk1=-12.5°,γkN为-14°或-13°，也可以是其他任务设计时感兴趣的初始路径角。3个不同初始路径角下，无路径约束的纵向可达区如图9所示。从图9可以看出，进入角更陡时，航程范围更窄。初始进入角对航程的影响更大，对于可达的最大/小开伞高度影响较小。

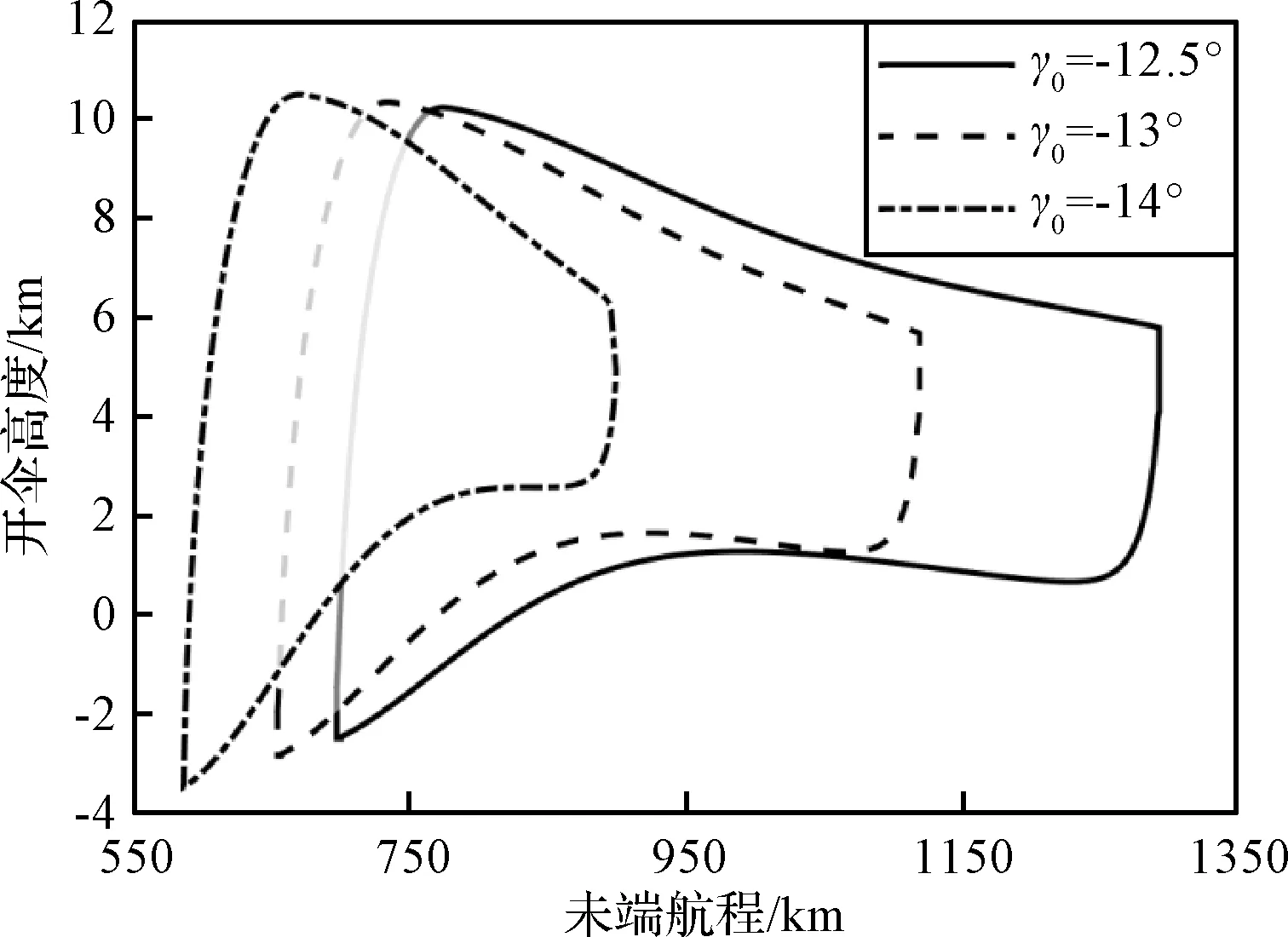
图9 不同初始航迹角下的纵向可达区Fig.9 Reachable area with different γ(τ0)

5 结 论

针对火星大气进入段飞行器的飞行能力分析问题，提出一种基于解析同伦法的纵向可达区(开伞点高度-航程剖面)生成方法。在纵向动力学背景下，考虑数值延拓的效率和可靠性，首先为无路径约束的最大/最小开伞高度、最大/最小航程问题分别构造最优解已知的初始辅助优化问题，并以此为出发点最终求取原最优问题的解。在求解4个子优化问题的基础上，通过构造合适的同伦参数，延拓出纵向可达区，避免了对可达区内部点可行性的验证。仿真结果表明，该方法有效避免了最优问题协态初值猜测困难的问题，同伦求解过程稳定。可以快速求取任意初始路径角下的末端最大/最小航程问题、最大/最小开伞高度问题以及纵向可达区问题。未来可在本文研究的基础上，结合精确罚函数方法，进一步求得存在路径约束时的纵向可达区。