可重复使用运载器的耐坠毁缓冲装置的设计优化

雷 波，张 明，岳 帅

(南京航空航天大学飞行器先进设计技术国防重点学科实验室，南京 210016)

0 引 言

当前，科学技术的进步使得人类有能力着眼于更加遥远的太空环境，去进行各项航天活动。在探索宇宙空间的过程中，运载器起着运输航天设备及人员的重要作用，而传统运载器成本高且未能实现重复使用。为了降低航天成本，运载器重复使用技术成为国内外的一大研究热点，重复使用运载器系统，是未来中国航天运输系统的重要组成[1-3]。目前，SpaceX公司的猎鹰-9运载器已成功回收，极大地鼓舞了科研人员的信心。运载器回收过程中，根据任务需求返回原发射场或其他发射场[1]，并配备相应的着陆平台，着陆场地状态较好，但是由于运载器自身控制系统的局限性以及外界环境存在干扰，可能出现超过其缓冲系统设计工况的着陆状态，导致运载器回收质量欠佳甚至坠毁。鉴于此，如何对多种着陆工况进行综合考虑，以此设计缓冲装置，使运载器具有耐坠毁性的同时，软着陆性能最优，是一项十分关键的工作。

文献[4-5]设计了一种用于重复使用运载器的油液-蜂窝缓冲装置，采用分级优化策略对其进行了优化设计，并对其性能进行了分析。文献[6]设计了一种基于油液缓冲器的运载器外翻式着陆支架，并进行了样机的着陆试验。文献[7]对临近空间载人舱的软着陆系统进行了仿真及试验，并对其进行了着陆性能的影响因素分析。考虑到运载器与着陆器在着陆动力学上的相似性，可以参考着陆器的相关研究。文献[8-9]通过仿真及试验分析了蜂窝缓冲材料的力学性能。文献[10-11]对基于铝蜂窝缓冲器的月球着陆器着陆过程进行了理论及试验研究。文献[12]研究了多种工况参数对月球着陆器着陆性能的影响。文献[13]基于响应面模型对两种着陆模式下的腿式着陆器进行了构型优化。文献[14]结合Monte Carlo法对不定姿态下的着陆器缓冲机构构型进行了优化设计。文献[15-16]对带有变阻尼缓冲器的腿式着陆器进行了性能分析及参数优化。文献[17]设计了用于月球着陆器的磁流变缓冲器，利用模糊控制算法对其进行半主动控制，提升了着陆装置的性能。

上述工作或是仅对支柱式多级缓冲系统进行研究及优化，所涉及到的多级优化策略较为复杂，约束条件过多，耗时较长；或是仅对单一缓冲形式下的着陆机构进行研究及优化。对于外翻式着陆支架耐坠毁缓冲装置的设计及优化鲜有文章报道，鉴于此，本文基于结构形式较为复杂的外翻式着陆支架，提出一种两级耐坠毁缓冲装置，考虑多工况着陆条件，采用多学科协同优化方法对两级缓冲器参数进行优化，改善运载器着陆性能。

1 可重复使用运载器耐坠毁缓冲装置设计及动力学建模

1.1 可重复使用运载器耐坠毁缓冲装置

可重复使用运载器采用外翻式着陆支架，且利用辅助外壳作为其支撑结构，着陆支架可在外部指令的控制下，由其收放支柱实现展开或者收拢，图1为可重复使用运载器着陆支架示意图。

为实现正常着陆工况下缓冲装置的可重复使用，以及危险着陆工况下运载器的安全回收，提出了一种油气蜂窝串联两级缓冲装置。运载器处于正常着陆工况，仅有油气缓冲器工作，铝蜂窝不压溃；危险着陆工况下，油气式缓冲器与铝蜂窝缓冲器同时工作，确保运载器安全着陆，实现耐坠毁功能。

鉴于危险工况出现的概率较小，蜂窝缓冲器不宜影响整个机构的紧凑性，文献[4-5]中将蜂窝缓冲器置于缓冲支柱上的结构形式虽受力性能较好，但不能满足对于结构紧凑性的要求。本文将蜂窝缓冲器置于外翻式收放支柱与箭体连接的铰点位置，蜂窝缓冲器竖直布置在箭体内部。图2为蜂窝缓冲器安装位置的示意图。

图1 可重复使用运载器着陆支架示意图Fig.1 The figure of landing gear for reusable launch vehicle

图2 蜂窝缓冲器的安装位置Fig.2 The position of honeycomb damper

1.2 可重复使用运载器着陆动力学模型

运载器的四组支腿及缓冲装置对称分布在箭体结构上，整机具有对称性，主要研究平面空间1-2-1式和2-2式对称着陆模式[18]，建立其全机动力学模型。图3为运载器(以2-2式为例)着陆动力学模型，为了在符合实际情况的基础下对软着陆动力学模型进行简化，对所示的模型做出如下假设：

1)2-2式着陆情况下，先后着陆的两组着陆支架的受力具有对称性，将缓冲支柱受力在二维空间内进行简化；在对称面内将每组着陆腿下的辅助外壳受力在平面空间内简化[19]。

2)将运载器质量分为三个部分，分别为弹性质量、非弹性质量以及中间垫片质量[5]。弹性质量为蜂窝缓冲器所支撑的所有有效载荷；非弹性质量为油气缓冲器活塞杆、足垫以及其连接机构的质量；中间垫片质量为油气式缓冲器和蜂窝缓冲器之间的质量，包含油气式缓冲器外筒、收放支柱以及相应连接机构的总质量。

3)对弹性质量进行理想假设，作为刚体集中在机体重心处，非弹性质量被视为集中作用在足垫铰接点上，中间垫片质量位于中间垫片质心处。

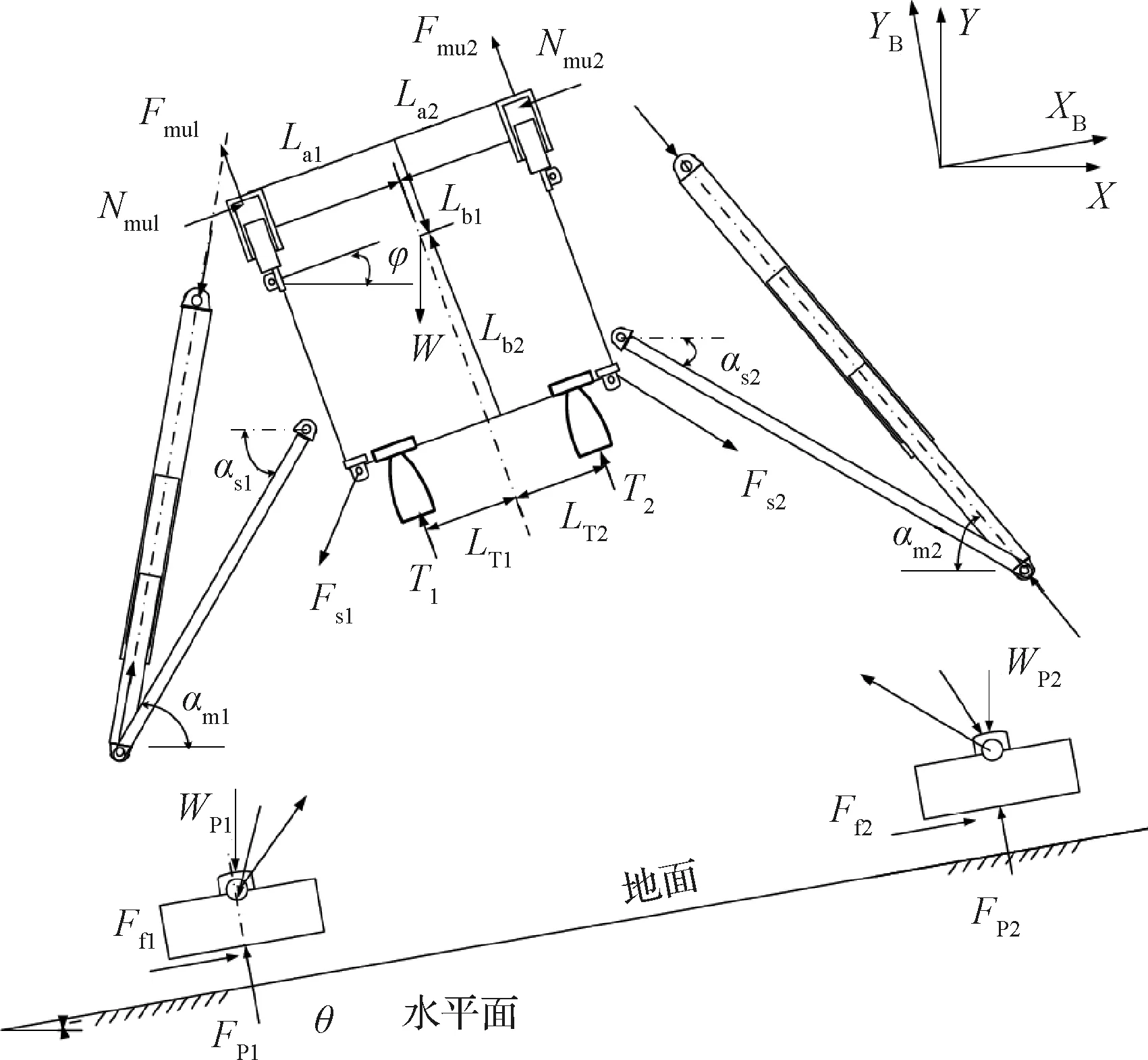
图3 运载器着陆动力学模型Fig.3 The dynamic model of vehicle landing

4)缓冲支柱均视为刚性，两端铰接，受力可近似为二力杆结构，仅受轴向力[19-20]；忽略辅助外壳质量，仅考虑承载。

5)只考虑弹性质量的铅锤运动、沿水平方向的运动，通过质心的俯仰运动。

6)基于经典赫兹理论求解足垫与陆面的接触力。

根据着陆器受力分离图，在惯性坐标系O-XY下，运载器软着陆弹性质量的动力学方程为：

Nmu1sinφ-Nmu2sinφ-Fs1sinαs1-

Fs2sinαs2-W+(T1+T2)cosφ

(1)

Nmu1cosφ-Nmu2cosφ-Fs1cosαs1+

Fs2cosαs2-(T1+T2)sinφ

(2)

μNmu2)La2+Nmu2Lb1+Fs1sin(αs1-φ)La1-

Fs1cos(αs1-φ)Lb2-Fs2sin(αs2+φ)La2+

Fs2cos(αs2+φ)Lb2-T1LT1+T2LT2

(3)

(4)

非弹性质量动力学方程：

Fsisinαsi-Wpi,i=1,2

(5)

(-1)iFsicosαsi

(6)

中间垫片动力学方程：

Fmdisinαmi-Wzi

(7)

(-1)iFmdicosαmi

(8)

式中：m为弹性质量，W为弹性质量重量，mpi为非弹性质量，Wpi为中间垫片质量重量，mzi为中间垫片质量，I为运载器转动惯量，Wzi为非弹性质量重量，θ为地面斜角，逆时针为正，φ为运载器姿态角，逆时针为正，Nmui为主支柱铰点对机体的侧向力，La1,La2为上铰点到箭体中轴线的距离,Lb1为上铰点至运载器质心的高度，Lb2为下铰点至运载器质心的高度，μ为蜂窝缓冲器内部摩擦系数，Fpi为地面对足垫垂直地面方向作用力，Ffi为地面对足垫沿地面方向作用力，Fmdi为油气式缓冲器等效缓冲力，Fmui为蜂窝缓冲器等效缓冲力，αmi为主支柱与水平面夹角，逆时针为正，αsi为辅助外壳与水平面夹角，逆时针为正，Fsi为辅助外壳对机体的等效作用力，LTi为微调火箭发动机距机体重心的距离，Ti为控制系统对着陆器作用力。

1.3 缓冲力模型

油气缓冲器为典型的单腔式常油孔缓冲器，其结构如图4所示。

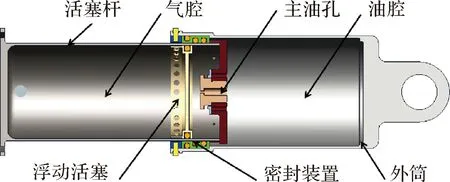
图4 油气式缓冲器结构Fig.4 The structure of oil pneumatic shock absorber

油气式缓冲器的缓冲力可表达为：

Frmi=Fh+Fa+Ff+Fs

(9)

式中：Fh为油液阻尼力，Fa为空气弹簧力，Ff为内部摩擦力，Fs为结构限制力。

不考虑回油时，油液阻尼力表达为：

(10)

式中：ρ为油液密度，Ah为压油面积，A+为正行程油孔面积，A-为反行程油孔面积，Cd为缩流系数，Sa为缓冲器压缩行程。

空气弹簧力表达为：

(11)

式中：H0=V0/Aa，Aa为压气面积，P0为初始气压，H0为初始气室高度，V0为初始气室体积，Patm为大气压力，γ为气体多变指数。

结构限制力表达：

(12)

式中：Sa0为油气缓冲器初始行程，Sa,max为油气缓冲器最大行程，Ks为缓冲器接触刚度。

铝蜂窝缓冲力表达为：

(13)

式中：Gmax为当前蜂窝最大压溃量，Fp为蜂窝压溃载荷，η为蜂窝动态压溃系数[21-22]，Sp为蜂窝压溃行程。

2 运载器软着陆地面工况及着陆性能判据

2.1 着陆工况条件

运载器正常着陆以及危险着陆工况初始着陆条件如表1所示。

表1 初始着陆条件Table 1 The initial landing conditions

2.2 软着陆性能判断指标

根据任务需求以及结构强度要求，参考深空探测器的相关性能指标，确定性能判据为以下几点[23]：

1)运载器不发生翻倒。即着陆过程中，运载器质心距含任意相邻足垫中心点的竖直平面的距离T的最小值Tmin应该大于0，否则认为运载器翻倒，并且Tmin越大，表示其越能抵抗翻倒。

2)运载器着陆加速度响应A的最大值Amax不超过7.0g，且越小越好。

3)运载器缓冲支柱所受载荷F的最大值Fmax导致的应力应避免结构破坏，且越小越好。

4)油气式缓冲器缓冲行程Sa的最大值Sa,max不超过其设计行程350 mm；蜂窝行程Sp的最大值Sp,max不超过其设计行程300 mm；在正常着陆工况下，蜂窝缓冲器不发生压溃，仅发生弹性形变。

5)着陆过程中，为防止运载器尾喷管撞击地面，运载器底部与着陆平面间距L的最小值Lmin保持在1000 mm以上，且越大越好。

3 两级缓冲装置的优化

3.1 蜂窝压溃载荷的确定方法

基于所述两级缓冲装置，对两级缓冲装置进行优化时，需满足两级缓冲间的协调性，即正常工况下，蜂窝材料不压溃。不同于与文献[4]通过约束蜂窝压溃行程来间接求解蜂窝力，本文将直接对蜂窝力进行求解，简化求解流程，此时蜂窝材料压溃载荷：

Fp=FZ,max

(14)

式中：FZ,max为正常工况下，蜂窝受载极值。

3.2 极限工况的选取

根据上述建立的着陆模型，基于表1所述的初始着陆工况参数，在大量不同的组合工况下进行运载器着陆动力学的仿真，并结合前文所述的软着陆性能指标，对各着陆响应进行对比分析，选取各着陆响应最恶劣的工况，最终形成了表2所示的4种极限工况：正常着陆时蜂窝最易压溃的工况1；运载器出现最大加速度Amax的工况2；缓冲支柱出现最大载荷Fmax，运载器出现离地最小距离Lmin，油气式缓冲器出现最大行程Sa,max，蜂窝缓冲器出现最大行程Sp,max的工况3；运载器出现Tmin，最易发生翻倒的工况4。

表2 极限工况系数Table 2 The parameters of critical landing conditions

注.表2中数字“4”代表运载器的四组着陆腿同时接触地面。

3.3 关键参数的识别

表3为两级缓冲装置的设计参数及其取值范围，采用最优拉丁超立方设计对油气缓冲器的活塞杆外径Ds、初始气压P0、正行程油孔直径Dh、初始气室高度H0以及蜂窝缓冲器的压溃载荷Fp在其各样本空间内抽取样本点，进行关键参数的识别，最终得到图5所示的帕累托图。

表3 设计参数的取值范围Table 3 The range of the design parameters

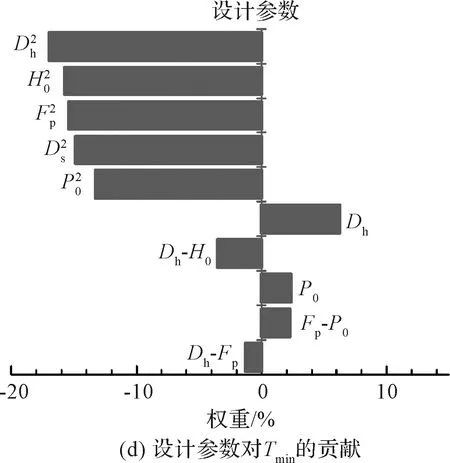
图5 帕累托图Fig.5 The Pareto graph

由图5可知，Ds，Dh，P0，H0，Fp对各着陆响应均有较大影响，且存在着一定的矛盾关系，故将其均视为缓冲装置的关键参数。

3.4 优化策略

为改善可重复使用运载器的着陆性能，取两级缓冲装置的关键参数作为设计变量，将最大化Tmin和Lmin，最小化Amax及Fmax作为优化目标，油气缓冲器最大行程Sa,max与铝蜂窝缓冲器最大行程Sp,max不超过其设计值作为约束条件，采用包含ASA算法与AMGA算法在内的多学科协同优化方法，对两级缓冲参数进行优化设计。将整个优化问题分为系统级和四个学科级：学科级一求解蜂窝力；学科级二分析工况2下的模型；学科级三分析工况3下的模型；学科级四分析工况4下的模型。

根据以上描述，在多学科协同优化方法基础之上，进行运载器软着陆性能的多目标优化，其数学模型如下：

系统级:

(15)

式中：X0为系统级设计变量组成的向量矩阵，Ji为系统级的一致性约束，εi为松弛因子[24]。

学科一：

MinJ1=(AX1+BFp1-X0)T(AX1+BFp1-X0)

d.v.X1=[Ds1Dh1H01P01]T

(16)

式中：X1为学科一设计变量组成的向量矩阵，

学科二至学科四：

(17)

式中：Xi为学科级i设计变量组成的向量矩阵。

3.5 基于代理模型进行求解

在优化过程中，各学科级优化需要不断调用动力学模型进行计算求解，此过程十分耗费时间，为了提高效率，缩短计算时间，采用径向基(Radial basis function,RBF)模型来近似代替各学科级下的动力学模型。采用最优拉丁超立方设计[25]在各模型对应的样本空间内采取2000个样本点和50组检验点，拟合出RBF预测模型并进行精度检测。采用标准误差RMSE和决定系数R2来对代理模型的精度进行评判：RMSE趋近于0，R2趋近于1，则代表拟合精度较好。其拟合精度如表4所示。

表4 RBF模型精度评判结果Table 4 The precision of RBF model

基于RBF代理模型，系统级采用存档微遗传算法(AMGA)，各子学科采用模拟退火算法(ASA)，对运载器软着陆过程中的多目标优化问题进行求解，最终得出运载器软着陆性能优化过程的流程如图6所示。

图6 优化流程Fig.6 The process of the optimization

3.6 优化结果

利用所述优化过程进行迭代求解，得到优化问题的Pareto非劣解集，绘制Pareto前沿如图7所示，对其Pareto前沿进行分析后，选择使得最大加速度响应Amax最小的解，最终得到其设计变量的初值和优化结果如表5所示。

为了进一步验证代理模型的准确性，将设计变量的最优解代入动力学模型进行求解，并将各着陆响应的计算结果与优化结果进行比较，结果如表6所示。由表6可知，采用的RBF模型具有较高的精度，各项响应误差均在2%以内，能够满足工程要求。

为了验证优化结果的有效性，将优化前的运载器的各项着陆性能指标与优化后进行对比分析，图8为优化前后运载器各着陆响应的对比图。

由图8所示的优化前后运载器各极限工况对应的着陆响应对比可知：优化后，工况2下运载器加速度响应最大值Amax由优化前的46.61 m/s2减小到31.92 m/s2；工况3下缓冲支柱最大载荷Fmax由优化前的754.44 kN减小为598.80 kN；工况3最小离地高度Lmin有所降低，由优化前的1456.80 mm减小为1430.68 mm，但是均在安全距离1000 mm以上；由于外翻式着陆腿展开半径大，结构稳定，且着陆场地条件较为理想，箭体不易发生倾覆，故优化前后工况4下的Tmin均为2191 mm。

图7 优化结果的Pareto前沿图Fig.7 The Pareto fronts of optimization

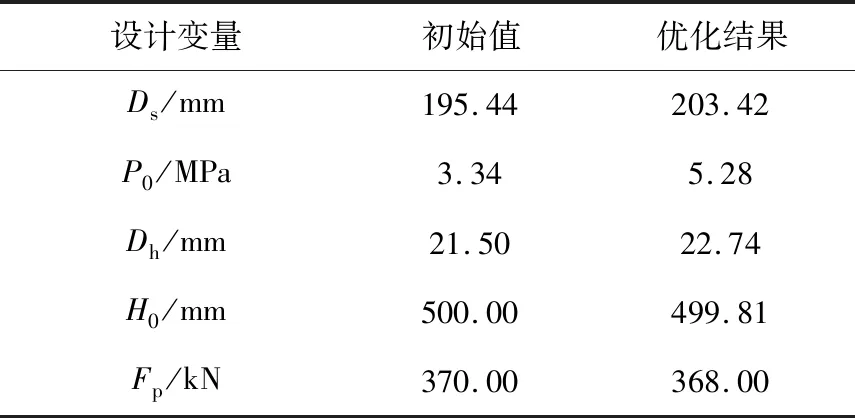
设计变量初始值优化结果Ds/mm195.44203.42P0/MPa3.345.28Dh/mm21.5022.74H0/mm500.00499.81Fp/kN370.00368.00

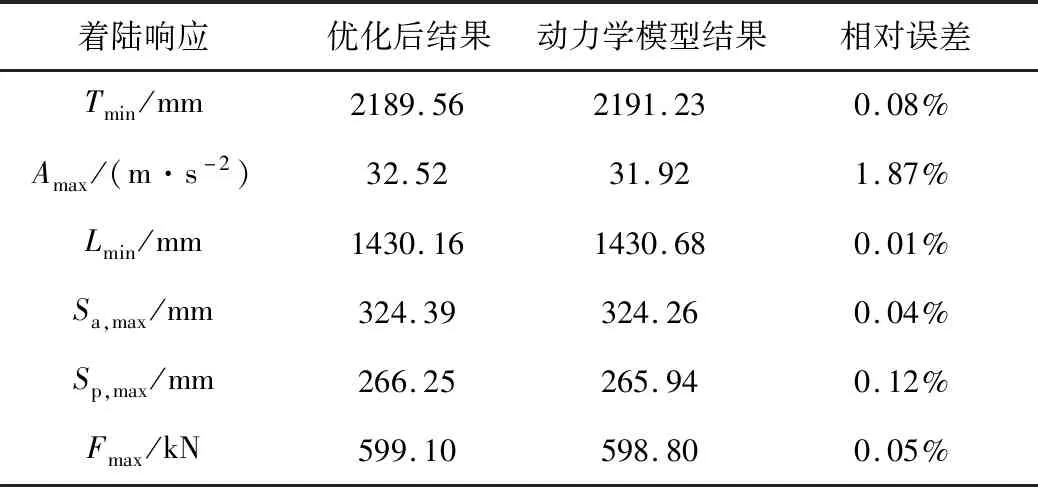
表6 代理模型计算结果与动力学模型计算结果对比Table 6 Comparison of optimization model and dynamic model

图8 优化前后运载器各着陆响应对比Fig.8 Comparisons of landing responses before and after optimization

综上所述，优化后，运载器的着陆性能得到了较为明显的提升。

3.7 两级缓冲装置的优势

相较于单独的油气缓冲器，当运载器处于危险着陆工况时，两级缓冲装置在降低运载器最大过载以及减小缓冲支柱载荷方面有着十分明显的优势。图9为运载器分别使用单独油气缓冲器和两级缓冲装置时在工况2下最大加速度响应对比图。

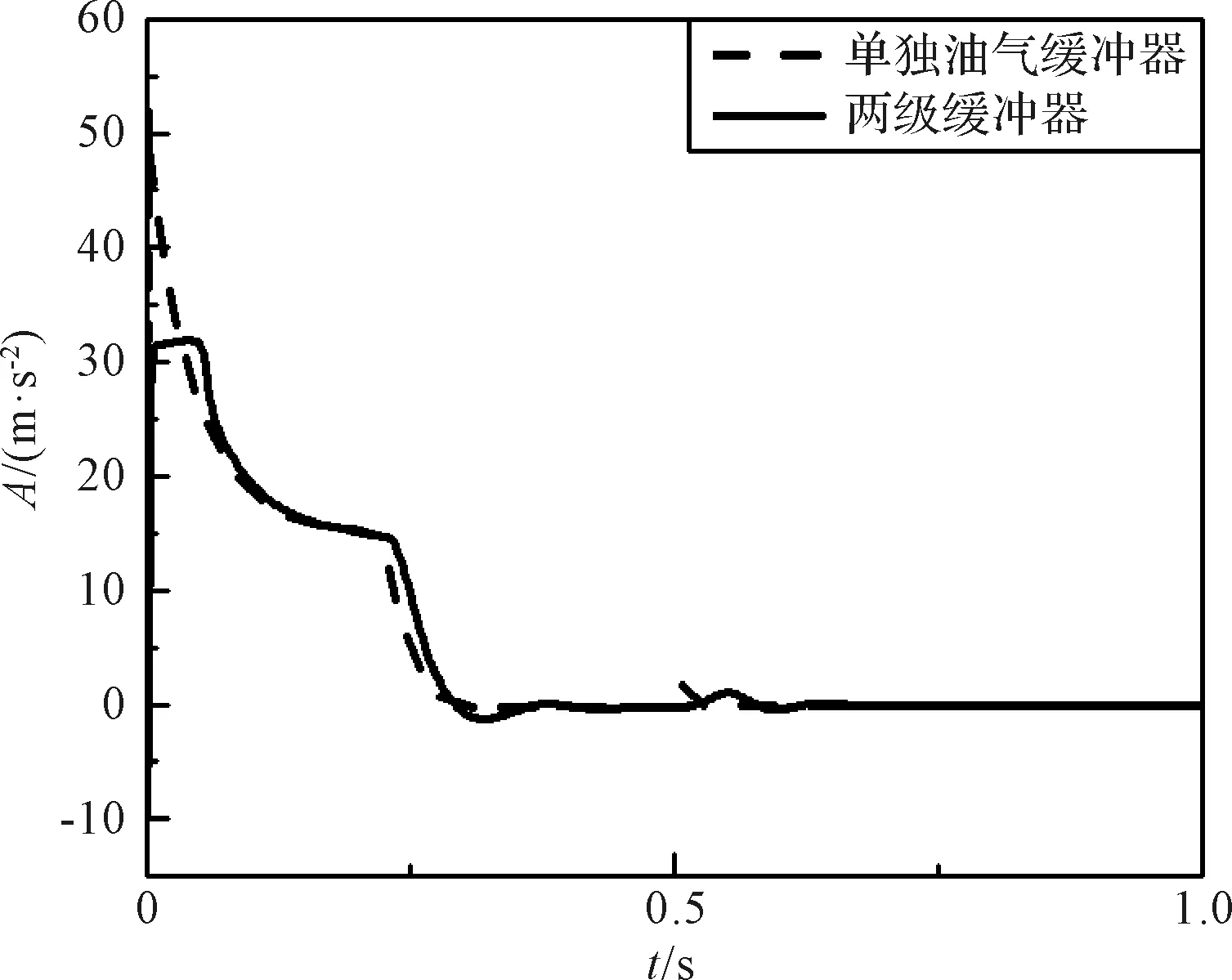
图9 单独油气缓冲器与两级缓冲装置下Amax对比Fig.9 The Amax with oil pneumatic shock absorber and two-stage shock absorber

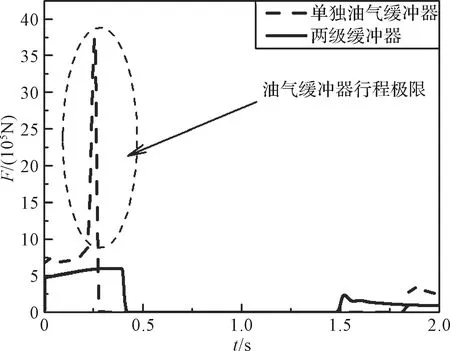
图10 单独油气缓冲器与两级缓冲器下Fmax对比Fig.10 The Fmax with oil pneumatic shock absorber and two-stage shock absorber

由图9可知，在仅使用油气缓冲器的情况下，运载器在工况2下的最大着陆加速度Amax大于使用两级缓冲装置的情况，达到了51.99 m/s2，使用了两级缓冲装置之后，其最大加速度Amax可降低至31.92 m/s2。

对比图10所示的工况3时两种缓冲装置下运载器缓冲支柱所受载荷，可知仅使用油气式缓冲器的情况下，运载器在危险工况下着陆时，缓冲器会达到极限行程，活塞杆与外筒发生碰撞，缓冲支柱载荷瞬间急剧增大，可能超过其结构强度限制，致使运载器损毁。在使用两级耐坠毁缓冲装置后，蜂窝缓冲器能吸收剩余功量，将载荷限制在安全范围之内，对着陆支架进行保护，提高运载器的回收成功率。

4 结 论

1)提出了一种用于外翻式着陆腿的油气-蜂窝两级耐坠毁缓冲装置，并建立了基于此耐坠毁缓冲装置的重复使用运载器软着陆动力学模型。

2)确定了蜂窝缓冲器与油气缓冲器之间的参数协调关系，在多种极限工况下，采用多学科协同优化方法对运载器耐坠毁缓冲装置进行了设计优化。结果表明，优化后运载器的最大着陆过载和缓冲支柱载荷有了明显降低。

3)两级耐坠毁缓冲装置相较于单独油气式缓冲器，能明显降低运载器着陆时的最大过载响应，减小缓冲支柱载荷，对缓冲支柱及其它相关结构起到保护作用，具有一定的耐坠毁性。