一种改进的永磁同步电机饱和数学模型

杨太鹏，宋 剑，曹博书

（1.中国民航大学飞行技术学院，天津 300300；2.中国南方航空股份有限公司机务工程部，广州 510470）

电机作为飞机全电化关键部件之一，是飞机舵机系统的核心元件，为飞机舵机操纵提供动力支持，其安全性直接关系到舵机系统的整体工作特性。永磁同步电机（PMSM,permanent magnet synchronous motor）具有短时过载能力强的优点，因此在飞机舵机系统等领域应用广泛。大电流重载情况下电机饱和严重，交直轴之间产生交叉耦合现象[1-2]，使传统PMSM 数学模型不能准确反映电机饱和时的电感特征，因此完善电机交叉饱和情况下的数学模型，可为重载情况下的电机驱动特性研究提供更加准确的模型依据[3-5]。

目前磁饱和模型的研究主要利用冻结磁导率法[6-7]，冻结电机某一运行状态的铁心磁导率，分别计算转子永磁体、交直轴电流单独作用时的磁链，由此计算出对应的电感值。

李和明等[8]使用冻结磁导率法计算出转子交直轴自感和交叉耦合互感值，电机的电感参数由3 张二维电感数表组成。张宇宁[9]对比研究了不同有限元方法计算电感的结果，证明了考虑交叉耦合效应可以提升电感值模拟精度，高精度电感同样需要3 张二维电感数表。李锦清等[10]为了提升电感计算精度，将互感分为交轴对直轴互感Ldq和直轴对交轴互感Lqd，共需要4张二维电感数表。文献[8-10]增加了仿真分析的查表量，控制器需要频繁查询电感来计算交直轴电压和电磁转矩，更多的查表量不仅占用了更多的控制器内存，而且降低了查表速度，削弱了控制器的响应速度。

为降低电感查表量，建立一种基于不对称交叉饱和电感的改进电机数学模型，令dq 轴自感仅与各自电流有关，dq 轴之间互感不对称。与文献[8]的冻结磁导率法相比，电感参数由两张二维表和两张一维表组成，简化了电感参数结构，可减小电感参数所占用的控制器内存空间，加快查表速度并降低查表量。以一台内埋式永磁同步电机为例，利用有限元法提取电流与磁链的关系曲线，将提取的参数曲线导入数学模型。通过Matlab 平台仿真实验，证明该数学模型能很好地反映电机在磁饱和条件下，电流与转矩、磁链与电动势的关系曲线，为电机饱和情况下的控制提供了简化可靠的数学模型依据。

1 建立PMSM 电机数学模型

常见的PMSM 数学模型为dq 轴数学模型，如图1所示，其中d 轴代表永磁体所在直轴，q 轴为超前于d轴90°电角度的交轴。

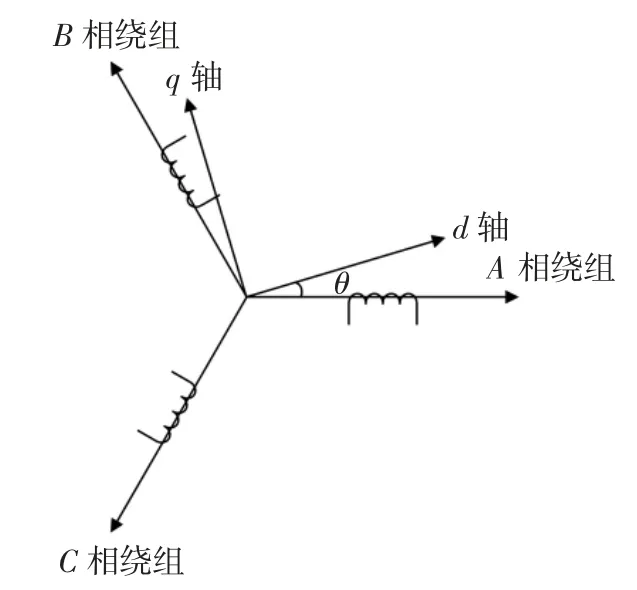
图1 永磁同步电机dq 轴数学模型Fig.1 PMSM math model foraxis d&q

1.1 不对称交叉磁饱和效应的电机数学模型

dq 轴磁路部分重合，且饱和情况下铁心的磁导率受电流影响较大，因此考虑交叉磁饱和的dq 轴磁链、电感与电流的关系为

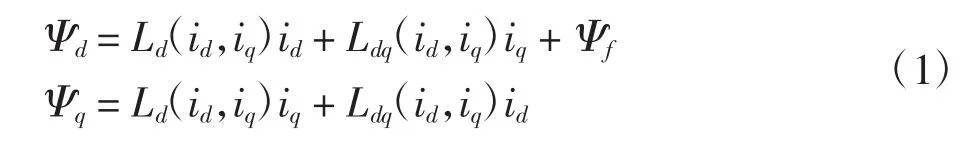
其中：Ψd为直轴磁链；Ψq为交轴磁链；Ψf为永磁体磁链；Ld（id，iq）、Lq（id，iq）和Ldq（id，iq）分别为d 轴自感、q 轴自感以及dq 轴互感。

传统的冻结磁导率法分别给定id和iq，模拟负载场情况下的磁路磁导率，进而计算交直轴自感和互感，分别得到两张自感和一张互感二维数表，由于传统的交直轴电感参数均与dq 轴电流相关，电感参数查表工作量大，为简化电感数表，对电感参数进行如下修正，即

其中：Ld（id，iq=0）为q 轴无电流时d 轴自感；Lq（iq，id=0）为d 轴无电流时q 轴自感；Ld（id，iq≠0）和Lq（iq，id≠0）为qd 轴施加电流时对dq 轴自感的影响，将式（2）代入式（1），简化为

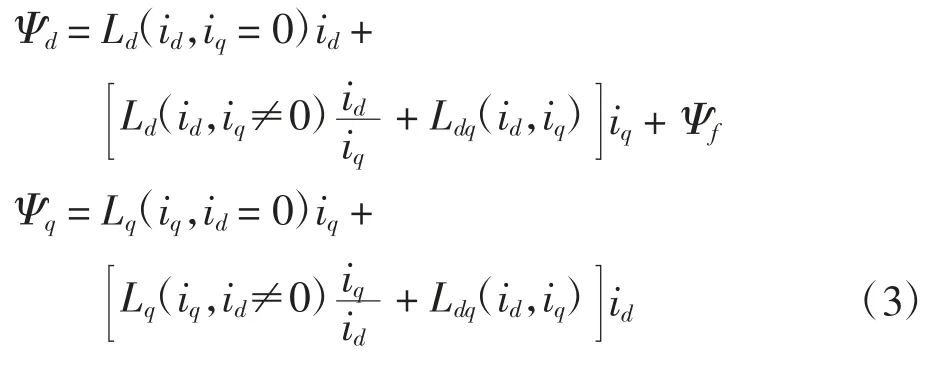
令

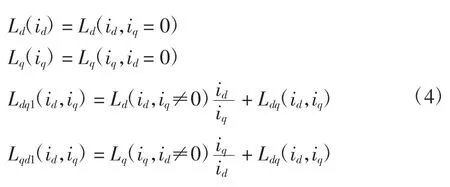
其中：Ldq1（id，iq）和Lqd1（id，iq）为dq 轴不对称互感，包含了dq 轴互感和dq 轴电流不为0 时对qd 轴自感的影响。

将式（4）代入式（3）可得dq 轴磁链方程为

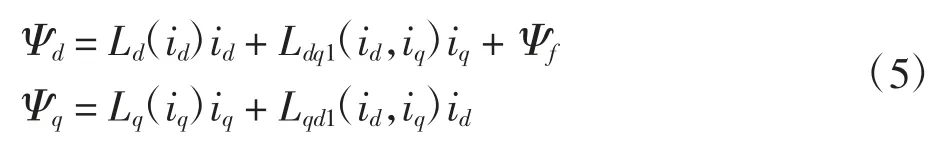
由虚位移法中磁链和电压的关系，将式（5）代入，可得改进模型的dq 轴电压方程为

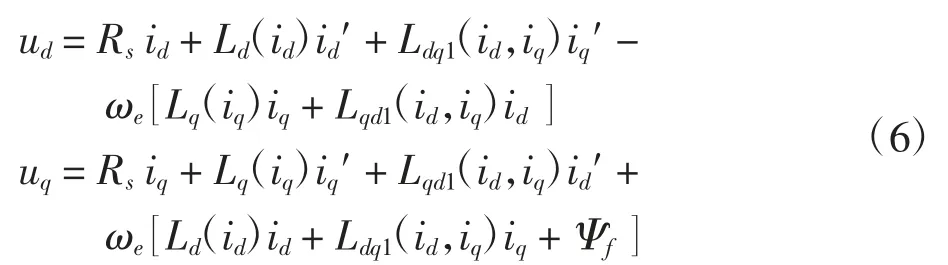
其中：uq、ud为交直轴电压；Rs为定子电阻；iq′、id′为交直轴电流随时间的导数；ωe为电角速度。

由电机电磁转矩与磁链的关系，将式（5）代入，可得改进模型的电机转矩方程为

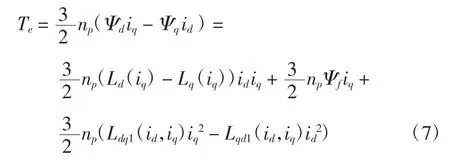
其中：np为电机极对数。式（7）中，第1 项为磁阻转矩，第2 项为永磁体转矩，第3 项为转子dq 轴磁场产生的转矩。

永磁同步电机数学模型由电气端和机型端组成，其中电气端为磁链-电流计算式（如式（5）所示）以及电压-电流式（如式（6）所示）。机型端为电磁转矩计算式（如式（7）所示）。由此式（5）～式（7）共同构成了考虑磁饱和情况的电机数学模型。

1.2 电感参数的提取方法

提取不同dq 轴电流状态的dq 轴磁链，根据式（5）分析dq 轴自感和不对称交叉耦合效应等效电感，计算如式（4）所述4 种电感参数的过程如下。

1）空载情况下，分析转子d 轴磁通，得到永磁体产生的磁通Ψf。

令q 轴电流为0，提取不同d 轴电流对应的d 轴磁链，则d 轴电感为

2）保持d 轴电流为0，提取不同q 轴电流对应的q轴磁链，则q 轴电感为

令d 轴电流不变，计算不同q 轴电流时的dq 轴磁链，与对应的d 轴电流为0 时的dq 轴磁链比较，则交叉不对称电感为

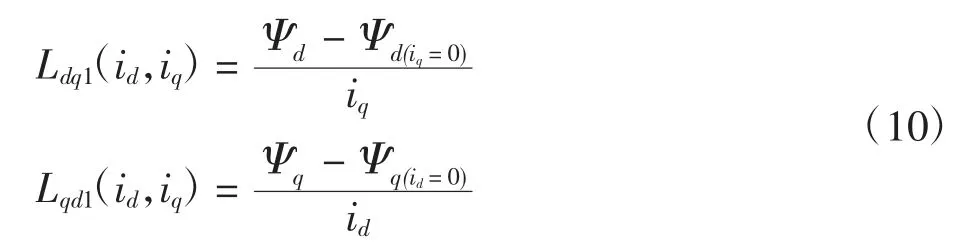
3）设定不同的d 轴电流，计算不同d 轴电流情况下，q 轴电流变化时的交叉电感。通过上述式（8）～式（10）可以计算出式（4）所需的4 种电感参数，其中交叉电感为二维数表，交直轴自感为一维数表。

2 Matlab 仿真平台下的磁饱和电机模型

Matlab/Simulink 仿真平台下，PMSM 模型采集电机三相绕组的端电压，计算对应的电流值，通过受控电流源输出电流，运用转矩计算模块计算对应的电磁转矩，具体计算流程如图2 所示。

在图2 所述流程中，设置起始dq 轴电流和转子位置θ 及转速ωe初始值id0、iq0、θe0、ωe0根据有限元分析结果，将电感与dq 轴电流对应关系导入lookup table查表模块，以便查找不同dq 轴电流对应的交直轴自感Ld（id）、Lq（iq）和不对称互感Ldq1（id，iq）、Lqd1（id，iq）。采集电机三相绕组端电压UABC通过dq 坐标变换成转子dq 轴电压Udq，采集上一采样周期转子dq 轴电流和对应电感，利用式（6）计算本周期dq 轴电流的微分值，利用采样步长积分计算本周期dq 轴电流值，经dq坐标反变换成电机三相绕组电流IABC，同时利用式（7）计算电机产生的电磁转矩Te。

图2 Matlab 仿真平台PMSM 电机模型计算框图Fig.2 PMSM calculating block diagram based on Matlab

3 仿真分析

利用有限元软件ANSYS EM 对一台内埋式永磁体PMSM 进行电磁分析，电机参数如表1 所示。

表1 永磁同步电机样机参数Tab.1 Parameter of a certain PMSM

根据式（8）～式（10），利用有限元法提取d 轴自感曲线、q 轴自感曲线与交叉电感曲线，如图3～图6 所示。

将电感参数导入lookup table 查表模块，进行如图2 所示的计算过程，根据不同交直轴电流查图3～图6所示的电流-电感参数表，获得Ld（id）、Lq（iq）、Ldq1（id，iq）、Lqd1（id，iq）参数，以便进行式（6）～式（7）的相关计算。为验证改进模型的准确性，采用基于受控电压源的电流滞环矢量控制系统，对比Matlab 仿真平台上建立的数学模型和有限元法分析出的电机电磁特性区别。不同d 轴电流情况下，q 轴电流与磁链、电磁转矩和交直轴电压的结果对比如图7～图10所示，其中：曲线为Matlab 仿真结果，阴影为有限元法计算结果。从图7 可看出，不同交直轴电流情况下，Matlab 仿真模型计算的交直轴磁链和有限元分析结果均能保持良好的一致性。从图8 可看出，不同交直轴电流情况下，仿真模型计算的电磁转矩和有限元分析结果基本一致，区别在于Matlab 仿真模型忽略了齿槽效应，因此计算的电磁转矩谐波较小，波形更加光滑。

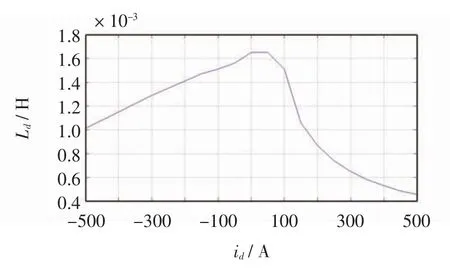
图3 Ld 与id 的关系Fig.3 Ld vs.id

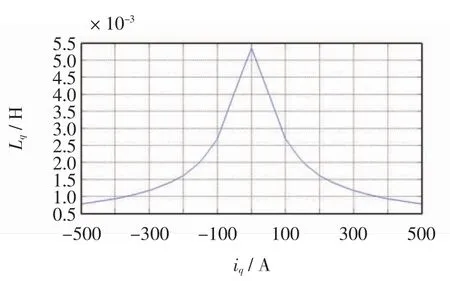
图4 Lq 与iq 的关系Fig.4 Lq vs.iq

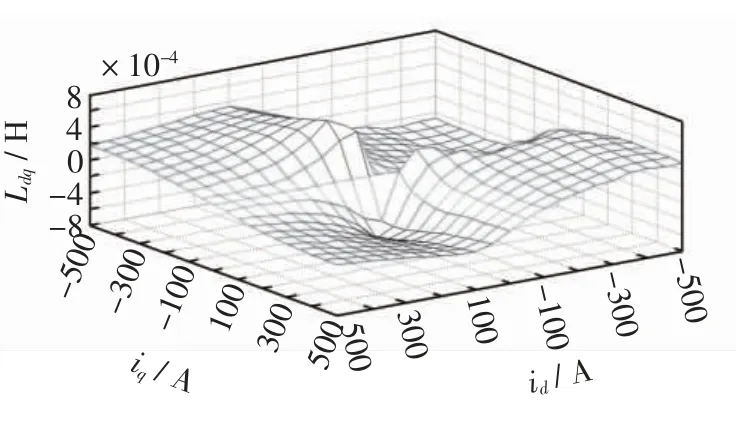
图5 Ldq 与id、iq 的关系Fig.5 Ldq vs.id&iq

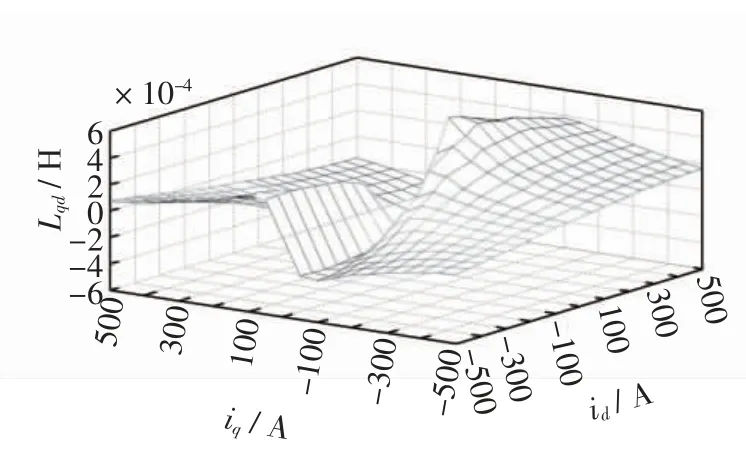
图6 Lqd 与id、iq 的关系Fig.6 Lqd vs.id&iq

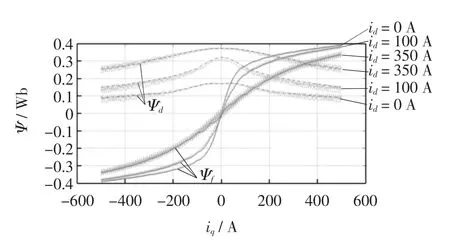
图7 有限元法和Matlab 模型仿真不同电流条件下dq 轴磁链对比Fig.7 Magnetic link comparison for axis d&q between FEM and Matlab

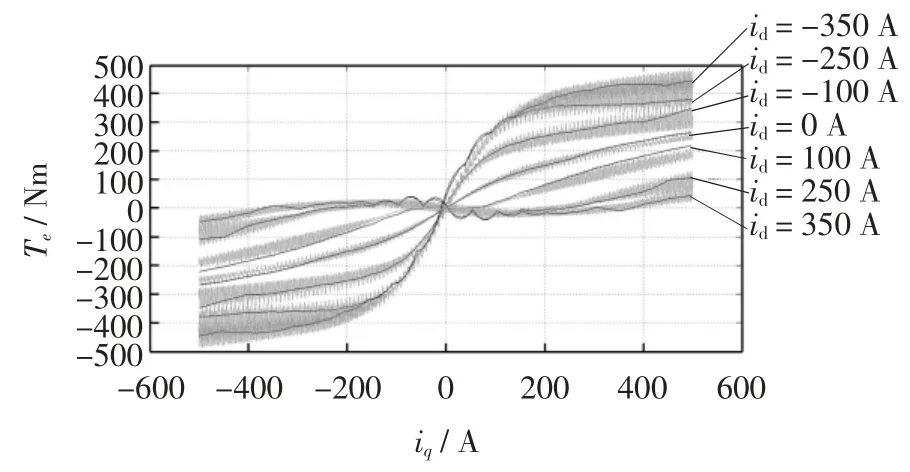
图8 有限元法和Matlab 模型仿真不同电流条件下dq轴电磁转矩对比Fig.8 Electric-magnetic torque comparison for axis d&q between FEM and Matlab

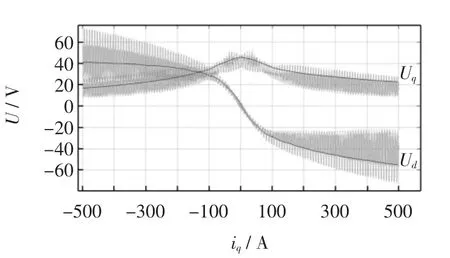
图9 有限元法和Matlab 模型仿真id=100 A 时iq 与电机反电动势曲线对比Fig.9 iq vs.back electromotive force under FEM and Matlab（id=100 A）

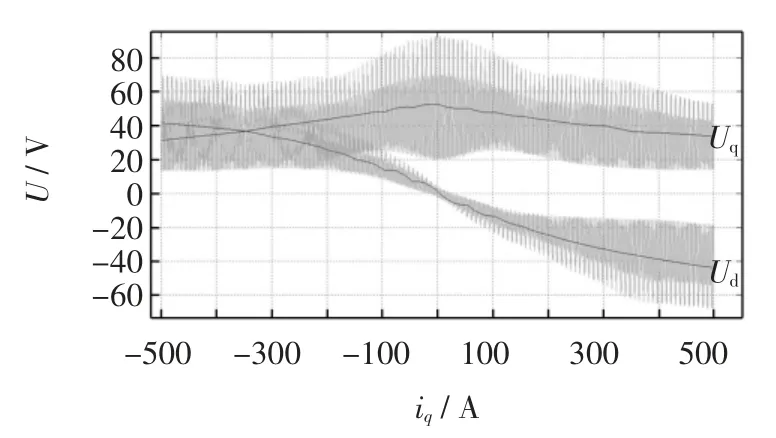
图10 有限元法和Matlab 模型仿真id=350 A 时iq 与电机反电动势曲线对比Fig.10 iq vs.back electromotive force under FEM and Matlab（id=350 A）

由图9～图10 可知，由于电机齿槽效应的影响，有限元软件计算出的磁链存在纹波，导致交直轴电压均带有纹波。由于改进模型主要研究饱和情况下的特点，故忽略齿槽效应，Matlab 仿真曲线较为平滑。

由图7 可知，改进模型得出的dq 轴电流与磁链的关系与有限元仿真结果一致，说明式（8）～式（10）具有良好的电感计算精度，式（5）中电流和磁链的计算关系准确。由图8 可知改进数学模型的电磁转矩计算结果和有限元分析结果基本一致，说明在不考虑转矩纹波情况下电磁转矩计算式（7）具有良好的计算精度。图9～图10 说明在id=100 A 和id=350 A 两种不同程度的饱和情况下，式（6）能准确反映电机的交直轴反电动势。综合图7～图10，说明由式（5）～式（7）组成的改进模型可准确反映电机饱和情况下的电磁特性，为电机控制提供了简化、可靠的数学模型基础。

4 结语

为研究交叉磁耦合效应对PMSM 电感的影响，完善了电机数学模型，利用有限元法提取了改进模型的电感参数曲线，在Matlab 仿真平台下与有限元分析结果进行比较研究。结果表明，改进模型能准确反映电机饱和特性，该模型电感参数由2 张二维表和2 张一维表组成，与传统的3 张二维电感参数表相比，减少了近1/3 的查表工作量，为实现电机在飞机舵机系统中的精确控制，特别是过载控制提供了准确简化、可靠的模型基础。