二元域上有限几何LDPC码的停止距离

高 有，马 赫

（中国民航大学理学院，天津 300300）

LDPC[1]（low density parity check）码因其接近香农限的良好性能而受到广泛关注。在研究和分析LDPC码在二元擦除信道上的译码表现时，发现其主要取决于校验阵中一种特殊的组合结构，即停止集[2]。

设一个线性码C 具有校验阵H，停止集是校验阵H 中某些列的列标集合，使得校验阵由这些列所构成的子矩阵没有Hamming 重量为1 的行，最小的非空停止集的大小为停止距离。最小Hamming 距离对于研究一个码在二元对称信道上的译码表现有很重要的作用。类似的，停止距离对于研究码在二元擦除信道上进行一些迭代译码的表现同样重要。

构造LDPC 码的方式有很多，其中通过有限几何来构造LDPC 码是一类重要的方法。Kou 等[3]利用有限几何中仿射空间与射影空间这两类空间中的点和线构造了性能很好的LDPC 码，并计算了码的最小Hamming 距离等参数。一个线性码的校验阵对应一个Tanner 图，图中最小圈的长称为围长，围长至少为6的正规LDPC 码其译码表现会更好。Tang 等[4]进一步基于有限几何中的flat 构造了码，其适用于很多的译码方法，如大数逻辑译码法、和积算法、置信传播法等，而这样构造的有限几何LDPC 码（FG-LDPC）通常会有很多长为4 的圈，其译码表现结果出乎意料。Kashyap 等[5]给出了基于组合设计所构造码的停止距离的下界，其结论可应用于有限几何构造的码。Xia等[6]进一步研究了有限几何LDPC 码停止距离的下界。

对于已有的基于二元域上仿射空间与射影空间中的μ-flat 和（μ+1）-flat 所构造的PDPC 码可找到一个停止集，其大小达到了有限几何LDPC 码停止距离所满足的下界，由此得出了这一类有限几何LDPC 码的停止距离。

1 停止距离及FG-LDPC 码简介

对于停止集及停止距离，下面给出具体的定义[6]。

定义1设C 是一个具有校验阵H 的[n，k]线性码，H 的行不是线性无关的。一个停止集S 是关于H的列标{1，2，…，n}的子集，满足由H 的这些列构成的子矩阵没有Hamming 重量为1 的行。

定义2最小的非空停止集的大小称为停止距离，记为s（H）。为了方便计算，对于停止距离还有另一种定义方式：设C 是一个具有校验阵H 的[n，k]线性码，停止距离s（H）是满足如下条件的最大的正整数，从H 中选出任意不超过s（H）-1 列构成的子矩阵至少有一行Hamming 重量为1。

仿射空间和射影空间[7]是有限几何中重要的两类，现对其简单介绍：

Fq是一个含有q 个元素的有限域（q 是一个素数的幂）。设AG（m，q）和PG（m，q）分别是Fq上的仿射空间和射影空间，统记为有限几何FG（m，q），由flat 组成。对0≤μ≤m，一个AG（m，q）中的μ-flat 是向量空间中的μ 维子空间或其陪集，一个PG（m，q）中的μ-flat 是向量空间中的μ +1 维子空间。特别的0-flat 和1-flat 分别代表FG（m，q）中的点和线。

在仿射空间和射影空间中有如下的计数定理[8]：AG（m，q）和PG（m，q）中μ-flat 个数分别记为NAG（μ，m，q）和NPG（μ，m，q），对0≤μ1＜μ2≤m 设NAG（μ1，μ2，m，q）和NPG（μ1，μ2，m，q）分别为AG（m，q）和PG（m，q）中给定μ2-flat 中的μ1-flat 的个数，N′AG（μ1，μ2，m，q）和N′PG（μ1，μ2，m，q）分别为AG（m，q）和PG（m，q）中包含给定μ1-flat 的μ2-flat 的个数。现简记N（μ1，m，q），N（μ2，m，q）分别为有限几何FG（m，q）中的μ1-flat 和μ2-flat 的个数，N（μ1，μ2，m，q）为给定μ2-flat 包含的μ1-flat 的个数，N′（μ1，μ2，m，q）为包含给定μ1-flat 的μ2-flat 的个数。根据flat 的可迁性有

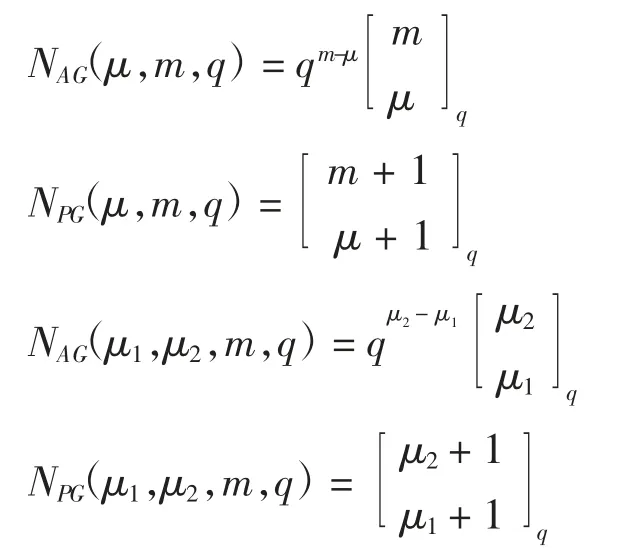
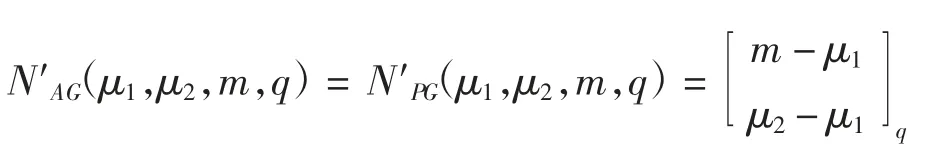
其中，高斯系数[7]为

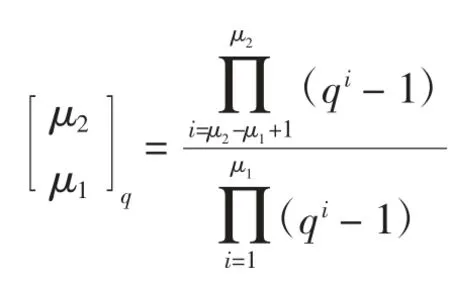
当μ1=0 时。

有限几何LDPC 码的介绍如下：

对0≤μ1＜μ2≤m，设n=N（μ1，m，q），J=N（μ2，m，q）。对于一个二元J×n 矩阵H(1)（μ1，μ2，m，q）=（hji），其行对应有限几何FG（m，q）中的μ2-flat，列对应μ1-flat。当第j 个μ2-flat 包含第i 个μ1-flat 时hji=1，否则hji=0。设H(1)（μ1，μ2，m，q）的转置为H(2)（μ1，μ2，m，q），则以H(1)（μ1，μ2，m，q）和H(2)（μ1，μ2，m，q）为校验阵的码称为有限几何LDPC 码，分别记为C(1)（μ1，μ2，m，q）和C(2)（μ1，μ2，m，q）。由有限几何的性质[7]，易发现只有当μ2=μ1+1 时，校验阵H(1)（μ1，μ2，m，q）和H(2)（μ1，μ2，m，q）的围长为6，其余情况均为4。

设码C(1)（μ1，μ2，m，q）和C(2)（μ1，μ2，m，q）所对应校验阵H(1)（μ1，μ2，m，q）和H(2)（μ1，μ2，m，q）的停止距离分别记为s（H）和s（HT）。根据文献[6]可知：对C(1)（μ1，μ2，m，q），s（H）≥N′（μ2-1，μ2，m，q）+1；对C(2)（μ1，μ2，m，q），s（HT）≥N（μ1，μ1+1，m，q）+1。

一个码的停止集和停止距离是与校验阵相关的，因此，停止距离不能超过一个码的最小Hamming 距离[8]。上述的有限几何LDPC 码在一些特殊情况下，最小距离已知。如文献[3]得出了点与线构造的LDPC 码的最小距离，且在仿射空间中构造的码C(1)（0，μ2，m，2）（其中μ2＞1）是μ2-1 阶的Reed-Muller 码[9]，而Reed-Muller 码的最小距离也已知，同样易得出上述情况下码的停止距离。

2 码C(1)（μ，μ+1，m，2）的停止距离

为得到有限几何FG（m，2）上码C(1)（μ，μ + 1，m，2）（其中0≤μ ＜μ + 1≤m）关于校验阵H(1)（μ，μ + 1，m，2）的停止距离s（H），首先给出如下引理。

引理1设e1，e2，…，em是二元域F2上向量空间的一组基（ei的第i 个位置为1，其余位置为0，i=1，2，…，m）则：

1）由eμ+1，eμ+2，…，em的线性组合构成的两两线性无关的非零向量共有M=2m-μ-1 个，记为a1，a2，…，aM；

2）向量组{e1+a1，e1+a2，…，e1+aM}中任意3 个向量线性无关。

对引理1 中的2）的证明如下：设向量组A={e1+a1，e1+a2，…，e1+aM}，假设A 中存在3 个向量线性相关，不妨设e1+ai∈A（i=1，2，…，M）可由向量e1+aj，e1+ak∈A（1≤i≠j≠k≤M）线性表示，于是在二元域F2中必有

e1+ai=（e1+aj）+（e1+ak）=aj+ak而由引理1 中的1）可知a1，a2，…，aM，是由eμ+1，eμ+2，…，em构成的两两线性无关的非零向量，矛盾。故向量组A 中任意3 个向量线性无关。

根据引理1 可得到如下引理。

引理2设e1，e2，…，em是向量空间中的一组F2的基，对0 ＜μ ＜μ + 1 ＜m，设如下矩阵表示

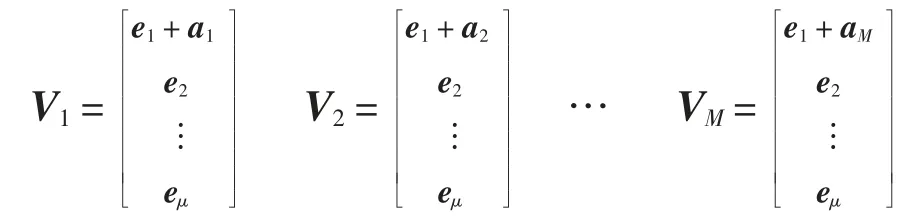
其中：M=2m-μ- 1；a1，a2，…，aM是由eμ+1，eμ+2，…，em的线性组合构成的两两无关的非零向量，则V1，V2，…，VM中的任意两个均包含在一个μ + 1 维子空间中，共有个不同的μ + 1 维子空间。

由维数公式可知：dim（Vi∪Vj）=dim（Vi）+dim（Vj）-dim（Vi∩Vj）=μ+1。

故V1，V2，…，VM中的任意两个均包含在一个μ +1 维子空间中且最多有个。

对任意的Vi，Vj，Vk，Vl，不妨令i≠j，k，l 且k≠l，设包含Vi，Vj的μ+1 维子空间为U1，包含Vk，Vl的μ +1 维子空间为U2，可写出具体的矩阵表示为

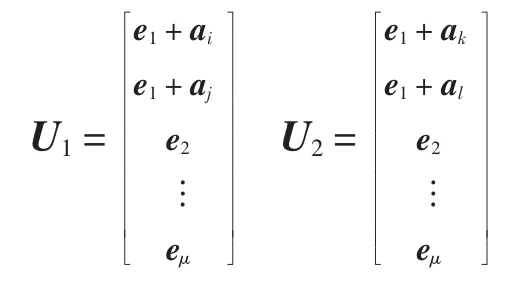
为证明U1，U2是不同的μ+1 维子空间，只需证e1+ai不能由U2线性表示，根据向量的形式及引理1 的结论，易看出e1+ai不能由U2线性表示，即U1，U2是不同的μ+1 维子空间。故这个μ+1 维子空间互不相同。

根据以上引理得出主要结果：

定理1对于有限几何FG（m，2）上的码C(1)（μ，μ +1，m，2）（0≤μ ＜μ + 1≤m）关于校验阵H(1)（μ，μ +1，m，2）的停止距离s（H）=2m-μ。

证明：当μ =0 或μ +1 =m 时，由文献[6]可知结论成立；当0 ＜μ ＜μ+1 ＜m 时，根据文献[6]及以上的计数定理有结论：s（H）≥N′（μ，μ + 1，m，2）+1=2m-μ。

故对于码C(1)（μ，μ + 1，m，2）的校验阵H(1)（μ，μ +1，m，2）只需找到一个大小为2m-μ的停止集即可。

下面在射影空间中进行讨论：

包含V 的μ + 2 维子空间共有M=N′（μ + 1，μ +2，m，2）=2m-μ-1 个，于是可将包含V 的μ + 2 的维子空间表示为

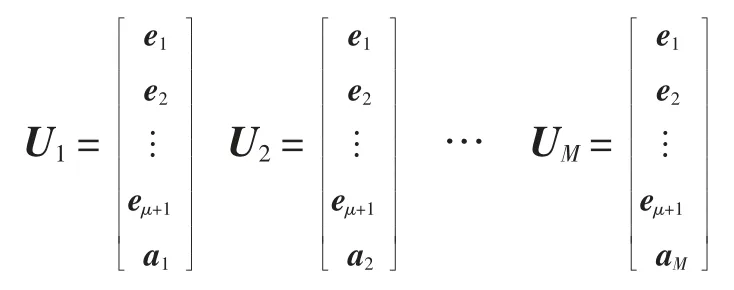
其中，a1，a2，…，aM是由eμ+2，eμ+3，…，em+1，的线性组合构成的两两无关的非零向量，显然U1，U2，…，UM均包含V 且两两不相同。从每个U1，U2，…，UM中选出一个包含在其中的μ+1 维子空间，可表示为

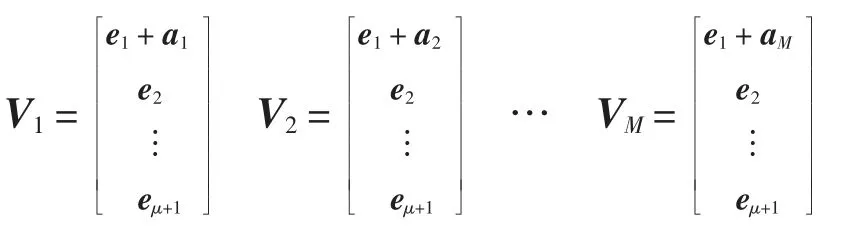
由引理2 可知V1，V2，…，VM中的任意两个均包含在一个μ + 2 维子空间中，共有个且互不相同，于是V1，V2，…，VM，V 中任意两个均包含在一个μ + 2 维子空间中，且这些μ + 2 维子空间互不相同。而在射影空间PG（m，2）中，μ-flat 和（μ + 1）-flat 分别代表向量空间中的μ + 1 维子空间和μ + 2 维子空间。校验阵H(1)（μ，μ+1，m，2）的行和列分别对应（μ+1）-flat和μ-flat，于是按照上面选取的子空间即μ-flat 可从H(1)（μ，μ + 1，m，2）中选出相应的列构成子矩阵，其没有

中的μ 维子空间用Hamming 重为1 的行，即存在大小为2m-μ的停止集。

类似地，对于仿射空间AG（m，2）仍然可找到大小为2m-μ的停止集。

综上所述，C(1)（μ，μ + 1，m，2）的停止距离s（H）=2m-μ。

3 结语

文献[6]得到了有限几何LDPC 码的停止距离的下界，利用其已有结论，并通过对仿射空间与射影空间中一些flat 具体形式的刻画，对应到码的校验阵中可找到一个大小达到停止距离下界的停止集，从而得出了某些特殊情况下二元域上有限几何LDPC 码的停止距离。