解三角形易错点“集结号”

■河南省固始县慈济高级中学 王 珩

我们知道,正弦、余弦定理的主要用途是解三角形,这类问题看似容易,其实却暗藏杀机,稍不留意,便会造成错解。本文给出几例,以期帮助同学们认清正余弦定理应用中的易错点。

易错点1 利用正弦定理求三角形的内角时丢解

例1在△ABC中,B=30°,AB=,AC=2,求△ABC的面积。

错解：由正弦定理,得,故C=60°,A=90°。

剖析：本题错误的原因是利用正弦定理求C时丢了一解。事实上,由sinC=可得C=60°或120°,这两个结果都符合题意。

正解：由正弦定理,得。又因为AB＞AC,所以C=60°或120°。

当C=60°时,A=90°,则

当C=120°时,A=30°,则

故△ABC的面积为

友情提示：在利用正弦定理求角时,由于正弦函数在(0,π)内不严格单调,所以角的个数可以不唯一,这时应注意借助已知条件加以检验,务必做到不漏解、不多解。

易错点2 忽视三角形的内角和定理

例2在△ABC中,C=3B,求的取值范围。

错解：由正弦定理,得：

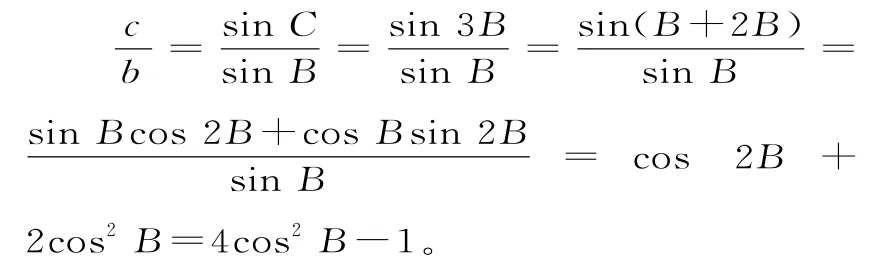
因为0≤cos2B≤1,所以-1≤4cos2B-1≤3,0＜≤3。

剖析：在上述解题过程中得到=4cos2B-1后,忽略了三角形内角和为180°及隐含的A,B,C均为正角这一条件。

正解：由正弦定理,得：

因为A+B+C=180°,C=3B,所以0°＜B＜45°,即＜cosB＜1。

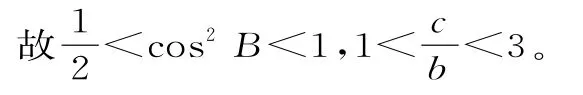
友情提示：在解三角形问题时,应注意A+B+C=180°,且A＞0°,B＞0°,C＞0°。

易错点3 忽视三角形的三边关系

例3设2a+1,a,2a-1为钝角三角形的三边,求实数a的取值范围。

错解：因为2a+1,a,2a-1是三角形的三边,所以解得a＞。

由题意知2a+1是三边长的最大值,设其所对角为θ。

因为2a+1,a,2a-1 是钝角三角形的三边,所以cosθ＜0。

故a的取值范围是＜a＜8。

剖析：错解中求得的a＞不是2a+1,a,2a-1表示三角形三边的等价条件。

正解：因为2a+1,a,2a-1是三角形的三边,所以

解得a＞,此时2a+1最大。

要使2a+1,a,2a-1 表示三角形的三边,还需a+(2a-1)＞2a+1,解得a＞2。

设最长边2a+1所对的角为θ,则：

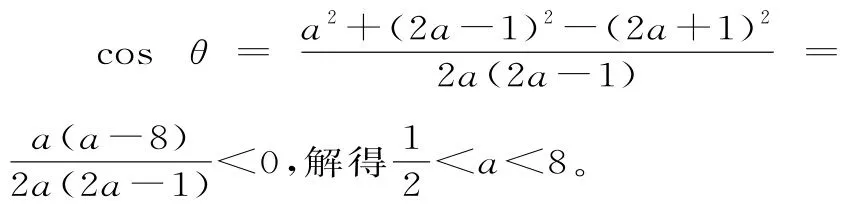
故a的取值范围是2＜a＜8。

友情提示：在求有关参数范围时,不可忽略三角形的三边固有的关系,否则会使某些变量的范围变大。

易错点4 忽视题设中的隐含条件

例4在△ABC中,已知A＞B＞C,且A=2C,b=4,a+c=8,求a,c的长。

错解：由正弦定理得因为A=2C,所以,a=2ccosC。

又因为a+c=8,所以

由余弦定理及a+c=8,b=4得：

当c=时,a=8-c=；

当c=4时,a=8-c=4。

故a=或a=c=4。

剖析：题设中条件A＞B＞C,等价于a＞b＞c,错解忽视了这个隐含条件。

正解：由上面的解法,由③得c=或c=4。

因为A＞B＞C,a+c=8,所以a＞4＞c,c=,a=8-c=。

故a=,c=。

友情提示：数学题中的每一个条件都不容忽视,解题时必须仔细推敲,谨防犯顾此失彼的错误。

易错点5 等式变形时随意约去公因式

例5在△ABC中,若(a-ccosB)sinB=(b-ccosA)sinA,判断△ABC的形状。

错解：由正弦定理及余弦定理知,原等式可化为：

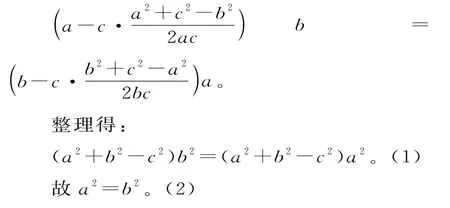
三角形为等腰三角形。

剖析：(1)化为(2)不是等价变形,因式a2+b2-c2可以为零,所以不可轻易约去。

正解：由正弦定理及余弦定理知,原等式可化为：

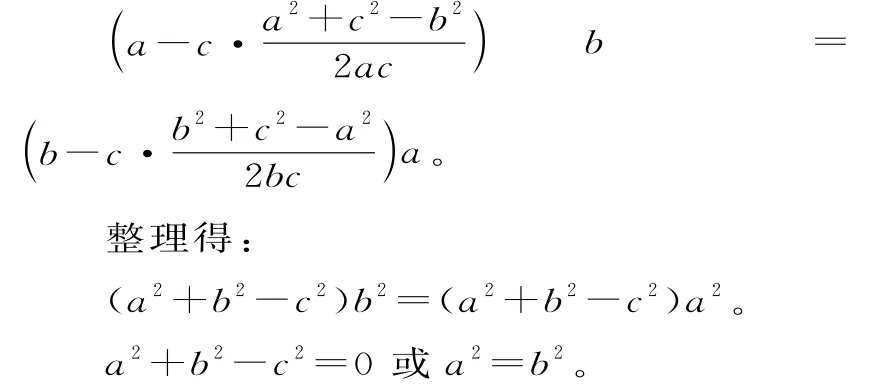
三角形为直角三角形或等腰三角形。

友情提示：解决此类问题的基本方法是将已知的边角关系式化为一边为零,另一边为三角式的乘积的形式或平方和的形式,或另一边为关于三边的多项式。注意不能随意约去公因式,否则结论便不完整了。