蒸汽射流喷嘴的排布优化设计

朱从云， 黄盼许， 黄其柏

(1.中原工学院 机电学院， 河南 郑州 450007； 2.华中科技大学 机械科学与工程学院， 湖北 武汉 430074)

近年来我国航空事业不断发展，飞机数量越来越多，冬季除冰的需求量越来越大[1]。我国飞机除冰多用除冰液，成本高且对环境污染大[2-3]。蒸汽射流除冰是一种高效清洁的除冰方式[4]。采用高温蒸汽射流除冰可节省成本，提高效率，且在保护环境方面具有重要意义。加强蒸汽射流除冰技术的研究，对提高除冰车性能具有较大的意义。采用蒸汽射流除冰需要配备蒸汽发生装置、蒸汽传输导管、压力温度监控装置、蒸汽射流喷头等。其中蒸汽射流喷头最为关键，喷头上喷嘴的布置方式对蒸汽射流除冰的影响最大。本文针对基于凝固和融化模型的蒸汽射流除冰系统[5]，基于单喷嘴结构确定喷嘴的分布，用Fluent软件对蒸汽射流除冰过程进行仿真，并对多喷嘴之间的干扰进行分析，并以文献[6]作参考来确定喷嘴排布的模型。

1 物理模型的建立

采用蒸汽射流除冰时，燃料通过导管被送入锅炉，锅炉产生的热水通过泵被送到热水喷头，热水经过喷射形成小水滴，与鼓风系统吹入的高温气体在压力通风系统中充分混合，经过加热线圈加热，产生的湿热蒸汽由传输系统输送到射流喷头，喷向工作表面，以达到除冰雪的目的[7]。蒸汽射流喷头为柔性气囊，蒸汽从顶部的进气口进入喷头。喷嘴被均匀布置在喷头底部，可向待除冰表面喷射高温饱和蒸汽。考虑到蒸汽射流喷头的全对称结构，为简化计算，在保证求解精度的前提下，本文以文献[8]作参考，在阵列孔纵截面处进行建模。图1所示为二维冰层融化多相流模型。相应的流体计算域如图2所示。

图1 二维冰层融化多相流模型

图2 流体计算域简图

2 网格的划分与计算模型的选择

2.1 网格的划分

考虑到建模区域的几何形状比较规则，本文采用结构化网格对建模区域进行网格划分。在图3所示的网格模型中，由于每个节点与其相邻节点之间的联系固定不变，且隐含在所生成的网格中，因此不必设置专用于确认节点之间关系的数据[9]。这种结构化网格模型具有以下特点：网格生成的速度快，网格质量好，数据结构简单，区域光滑程度与实际模型更接近，很容易实现区域边界的拟合[10]。

图3 网格模型

2.2 计算模型的选择

雷诺系数计算式为：

(1)

式中：L为圆管流动的特征长度；V为流体截面的平均速度；ρ为蒸汽的密度；μ为流体的动力黏度；v为流体的运动黏度。

针对标准的k-ε湍流模型，有

(2)

式中：Cμ为经验常数，Cμ=0.09。

流体的湍动能为：

(3)

湍动能耗散率为：

(4)

流体的湍流强度为：

(5)

当V=7 km/h，L=2 mm，v=1.5×10-6kg/(m·s)，ρ=1.672 kg/m3时，根据式(1)-式(5)可算出：I=3.44%;k=17.32 m2/s2；ε=84 673.84 m2/s3；Re=308 049.28。显然，雷诺系数远远大于10 000，流体为湍流型。因此，根据文献[11],本文计算模型选择湍流模型。

针对标准的k-ε湍流模型，湍动能k的输送方程为：

ρε-YM+Sk

(6)

式中：ui为微元表面dS上流体的速度；μt为流体的动力黏度，在k-ε模型中等于μ；YM为可压缩湍流中脉动扩张的贡献；Gk为平均速度梯度引起的湍动能；Gb为浮力引起的湍动能；σk为湍动能的Prandtl常数，σk=1.0；Sk为自定义的湍动能源项。

耗散率ε的输送方程为：

(7)

式中：σε为耗散率的Prandtl常数，σε=1.3；Sε为自定义的耗散率源项；此外，两个系数分别为C1ε=1.44，C2ε=1.92。

3 仿真模拟及结果分析

3.1 偶数喷嘴均布排列

在图4所示的偶数喷嘴均布排列情况下，计算区域尺寸为440 mm×80 mm，10个直径为2 mm的喷嘴均匀排列，孔间距为40 mm，冰层厚度为8 mm，蒸汽射流的额定压力为0.3 mPa。

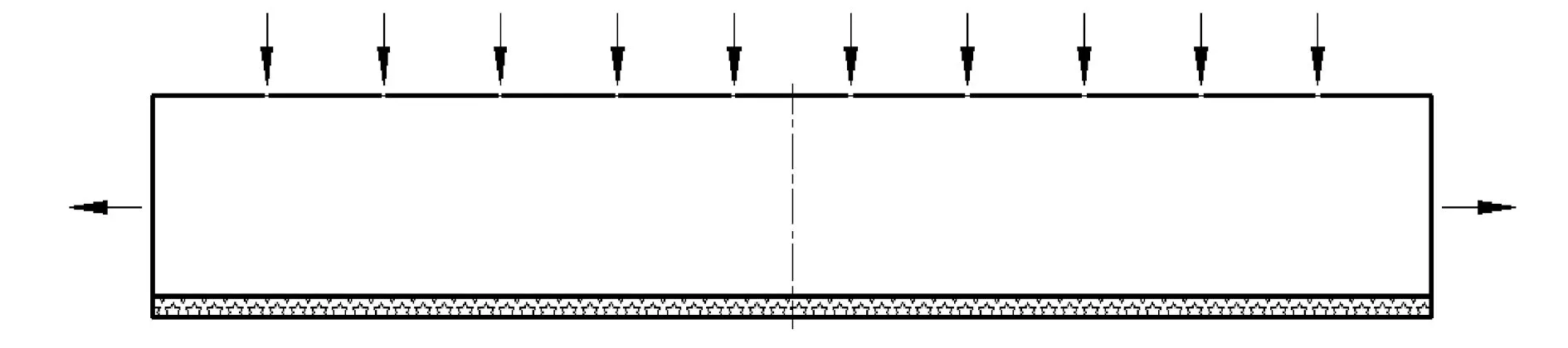
图4 偶数喷嘴均布排列示意图

将网格模型导入Fluent软件，经过0.1 s的迅速迭代，可得图5所示偶数喷嘴均布排列的温度场。

分析图5可知，在偶数喷嘴均布排列的情况下，温度场基本呈对称分布，各喷嘴的射流之间相互干扰；计算区域对称轴附近的干扰最剧烈，阻止了温度场的进一步扩散；在出口界面附近，蒸汽射流的溢流损失较明显，降低了蒸汽的利用率。

图5 偶数喷嘴均布排列的温度场

3.2 奇数喷嘴均布排列

(1) 在图6所示的奇数喷嘴均布排列情况下，计算区域尺寸为480 mm×80 mm，11个直径为2 mm的喷嘴均匀排列，孔间距为40 mm，冰层厚度为8 mm，蒸汽射流的额定压力为0.3 mPa。

建立奇数喷嘴均布排列的数值仿真模型，将模型导入Fluent软件，经过0.1 s的迅速迭代，可得图7所示奇数喷嘴均布排列的温度场。

图6 奇数喷嘴均布排列示意图

图7 奇数喷嘴均布排列的温度场

由图7可以看出，奇数喷嘴均布排列的温度场亦基本呈对称分布，只是在出口界面附近产生了干扰，且在两端边界处产生了一定的蒸汽射流的溢流损失。

对比图7与图5可知，与偶数喷嘴均布排列相比，奇数喷嘴的射流干扰和溢流损失均有所改善，其计算区域对称轴附近的冰层融化速率更高。因此，本文选择射流喷嘴的排列类型为奇数排列。

(2) 在射流喷嘴选择奇数排列的基础上，针对喷嘴均布排列具有射流干扰较强和溢流损失较大的不足，本文提出了奇数喷嘴均布排列非完全垂直射流的优化方案。

奇数喷嘴均布排列非完全垂直射流仿真模型是指，在奇数喷嘴均布排列仿真模型的基础上，将对称轴处的蒸汽射流角度设为0°，而使两侧蒸汽以60°的射流角度向对称轴方向喷射(见图8)。奇数喷嘴均布排列非完全垂直射流仿真模型的计算区域、冰层厚度、孔间距、喷嘴的数量和大小、除入口边界外的其他边界条件等，均与优化前仿真模型一致，只是改变部分蒸汽射流的角度。定义入口边界即可进行仿真。

将网格模型导入Fluent软件，经过0.1 s的迅速迭代，可得图9所示奇数喷嘴均布排列非完全垂直射流的温度场。

图8 奇数喷嘴均布排列非完全垂直射流示意图

图9 奇数喷嘴均布排列非完全垂直射流的温度场

从图9可以看出，奇数喷嘴均布排列非完全垂直射流的温度场分布已基本克服射流干扰，出口边界附近的蒸汽溢流损失比优化前有所减少，在除冰时间相同的情况下，冰层剩余量更少。分析可知，奇数喷嘴均布排列非完全垂直射流仿真模型的温度场分布更优，计算区域内平均温度较高，除冰更快，能够提高整车的除冰效率。

通过仿真模拟，对蒸汽射流喷嘴的排布进行了整体优化(见图10)。其设计面积为480 mm×480 mm，共有121个喷嘴，按11列交错排布，每列间隔为40 mm，以有效减小喷嘴之间的干扰。

图10 整体优化后蒸汽射流喷嘴的排布

4 结语

(1) 对蒸汽射流喷嘴的3种排布方式进行仿真，结果表明：奇数喷嘴均布排列非完全垂直射流的喷头计算区域温度场分布均匀，平均温度较高，冰层余量最小，能够满足对飞机机身快速除冰的需要。

(2) 采用蒸汽射流除冰，除冰完成后采用高温热风对机身表面进行处理，可防止机身二次结冰。

(3) 采用本文蒸汽射流喷嘴的优化排布方法，使喷嘴均布排列，可减少飞机机身除冰的蒸汽使用量，降低能源消耗，节约成本。