不同倾角裂隙砂岩单轴压缩颗粒流模拟分析
袁丽景
(河南理工大学 土木工程学院, 河南 焦作 454003)
天然岩体在长期受地质力作用后,其内部往往形成了许多微小的裂隙,这些裂隙被称为天然裂隙。在外荷载的作用下,岩体内部的天然裂隙起裂并扩展延伸直至贯通,最后岩体被破坏[1]。研究表明,岩体裂隙倾角对岩体裂纹扩展以及岩体强度会产生影响[2]。岩体裂隙的存在导致许多工程事故的发生,因此,研究裂隙岩体的强度和破坏规律,对预防工程事故的发生格外重要。对于裂隙岩体的研究来说,物理试验虽然结果比较直观,但是也存在许多缺点,比如试样制作周期较长、观察手段单一导致结果不理想、花费大量的人力物力等[3]。近年来,随着计算机技术的飞速发展,数值模拟方法在岩土工程中的应用也越来越广泛,基于离散元理论的二维颗粒流程序(PFC2D)成为解决岩体内部损伤问题的主流方法。在PFC2D中,平行黏结接触模型一次黏结键的破坏代表一次微裂纹的产生,宏观裂隙由许多微裂纹扩展贯通而成[4]。利用二维颗粒流程序(PFC2D)这个功能,可以对模型内部裂纹的发育和演化过程进行模拟,研究岩石破裂机理。本文采用二维颗粒流程序(PFC2D)对不同倾角预制裂隙的岩体进行单轴压缩数值模拟试验,以研究不同倾角裂隙岩体强度的变化规律以及裂纹的扩展形式。
1 颗粒离散元法
1971年,CUNDALL在法国国际岩石力学会议上提出了离散元法,后来这种方法经VOEGELE等人的发展,被广泛应用于岩土工程数值模拟中[5]。二维颗粒流程序(PFC2D)是基于离散元法的数值模拟方法。用二维颗粒流程序(PFC2D)构建的模型中,颗粒之间的相互作用用颗粒接触本构模型来描述,其中接触黏结模型和平行黏结模型最常用。在接触黏结模型中,颗粒与颗粒之间只要存在着接触,黏结键的断裂不会对材料的宏观刚度产生很大影响。但对于平行黏结模型来说,黏结键的断裂会立刻导致宏观刚度的减小。这与岩石的破裂机制相符。因此,模拟岩石材料平行黏结模型是更好的选择,此次数值模拟采用平行黏结模型[6]。本文试验所用的完整岩石试样模型如图1所示。该模型含有10 039个颗粒和25 710个接触。用二维颗粒流程序(PFC2D)创建裂隙、节理的方法有多种,比如可以通过弱化颗粒间的黏结、改变颗粒间的接触方式、 删除一定范围内的颗粒等[7]。此次模拟试验采用删除指定范围内颗粒的方法创建预制裂隙,即通过PFC内置fish语言,选定预制裂隙处的颗粒集合并删除这些颗粒。所形成的裂隙模型如图2所示,图中白色所显示的裂隙为删除颗粒之后所形成的预制裂隙。
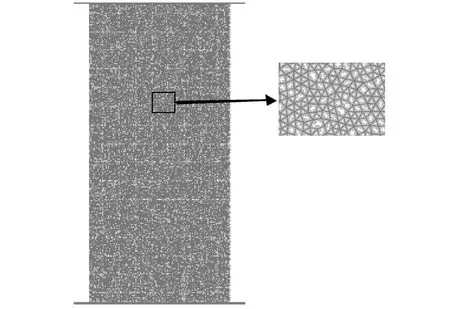
图1 完整岩石试样数值模型
2 含裂隙岩体模型的建立以及细观参数的标定
2.1 含预制裂隙岩体模型的建立
采用二维颗粒流程序(PFC2D)建立50 mm × 100 mm 的岩石力学标准岩样模型。首先生成4道墙体作为边界,围成50 mm × 100 mm 的矩形区域,随后在矩形区域内生成圆形颗粒,圆形颗粒的半径采用Rmin~Rmax的均匀分布,Rmin=0.3 mm,Rmax=0.45 mm。删除指定范围内的颗粒,分别生成倾角α为0°、15°、30°、45°、60°、75°、90°,长度为20 mm的预制裂隙,再删除矩形区域左右两侧的墙体,保留上下两侧的墙体,并给予上部墙体和下部墙体大小相等、方向相反的运动速度,以实现试样的单轴压缩加载,当应力降到峰值的70%时,数值模拟试验结束。不同倾角裂隙岩体试样如图2所示。岩体试样加载示意图如图3(裂隙倾角α=30°)所示。

(a) α=0° (b) α=15° (c) α=30° (d) α=45° (e) α=60° (f) α=75° (g) α=90°图2 不同倾角裂隙岩体试样

图3 岩体试样加载示意图(α=30°)
2.2 砂岩细观参数的标定
二维颗粒流程序(PFC2D)模型参数是基于离散元颗粒的细观参数,这些细观参数无法从室内试验直接获取。因此使用二维颗粒流程序(PFC2D)进行数值模拟试验时,不能直接采用室内试验获得的宏观参数,而需要找到与宏观参数相对应,适用于PFC2D模拟的细观参数[8]。只有选择合适的细观参数,才能准确还原宏观模型的力学特性。经过多次调试参数,最终得到图4所示的破坏模式、图5所示的应力-应变曲线、以及表1所示的宏观力学参数。此次模拟采用平行黏结模型,颗粒之间通过平行黏结不仅可以传递力的作用,还可以传递弯矩的作用[9]。数值模型的细观参数如表2所示。
3 颗粒流模拟试验结果分析
3.1 预制裂隙对裂纹扩展的影响
不同倾角裂隙岩体单轴压缩数值模拟试验裂纹扩展情况如图6所示。
由于预制裂隙的存在,裂隙端部出现应力集中,当应力超过临界值时,裂纹就会发生扩展[10]。因此,裂纹的衍生是从预制裂隙的端部开始的,随着荷载的增加,裂纹慢慢扩展,直到试样被彻底破坏。沿裂隙岩体对角线方向产生的裂纹最多,不同倾角预制裂隙岩体的破坏模式略有不同。从图6可以看出,当预制裂隙的倾角为0°、15°、30°时,裂纹扩展呈两个方向:一个方向近似垂直于主应力方向扩展,被称为翼裂纹;另一个方向与预制裂隙呈一定夹角方向扩展,被称为次生倾斜裂纹[11]。而当预制裂隙倾角分别为45°、60°、75°时,裂纹萌发于裂隙尖端,扩展的方向与裂隙走向大致一致,这种裂纹被称为次生共面裂纹。当预制裂隙倾角为90°时,裂纹的扩展几乎与完整岩体一致,破坏形态也几乎与完整岩体相同,说明90°裂隙的存在对岩体影响最小。通过单轴压缩数值模拟试验可知,模型在破坏过程中产生的裂纹主要为张拉破坏裂纹,少量的剪切裂纹贯穿其中,裂纹扩展和破坏的模式受预制裂隙倾角的影响。

(a) 数值模拟破坏模式 (b) 试验破坏模式 图4 砂岩数值模拟破坏模式与试验破坏模式
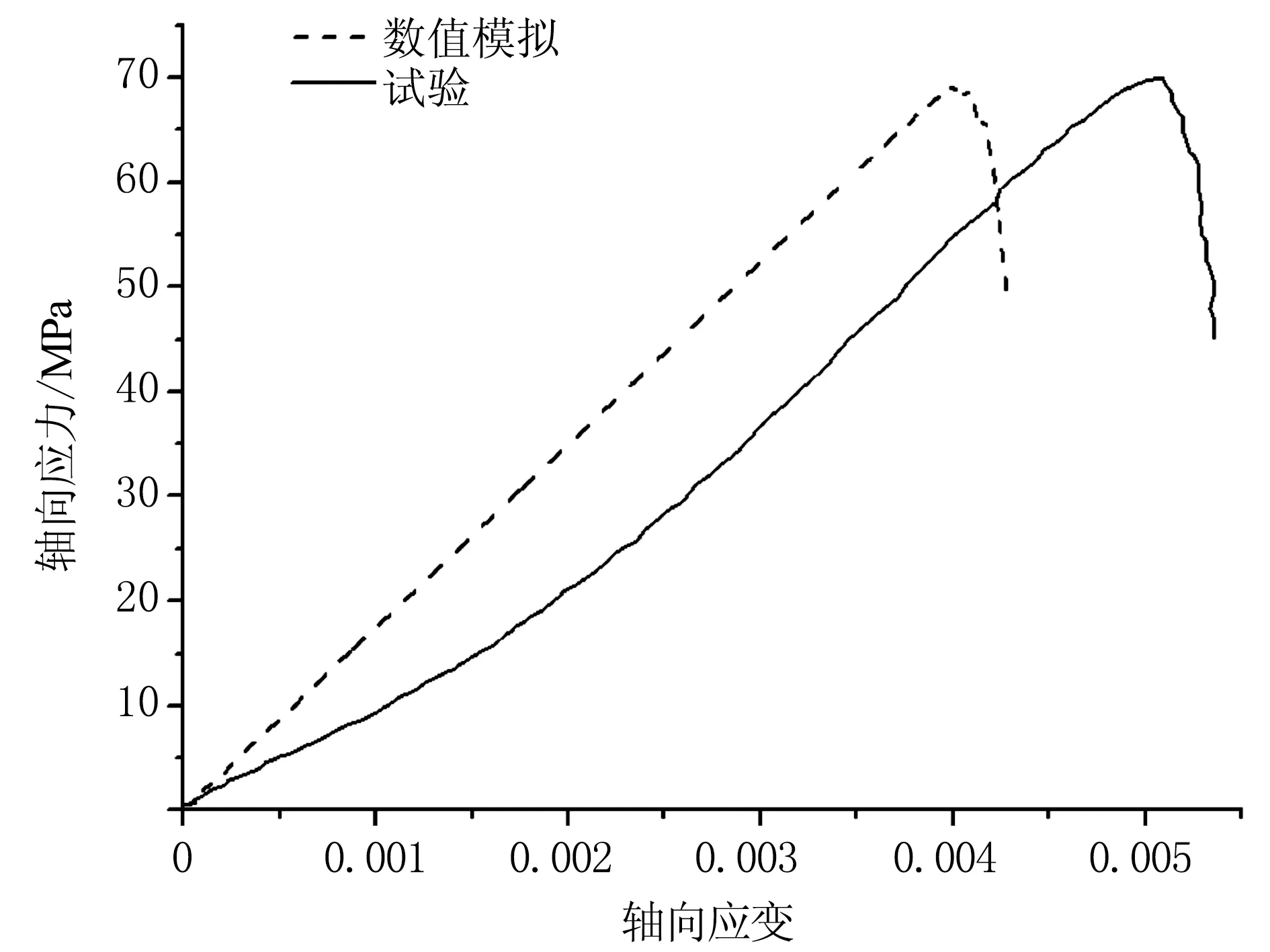
图5 单轴压缩数值模拟与试验应力-应变曲线图

表1 砂岩试验模拟参数对比表

表2 PFC2D模拟砂岩的细观参数
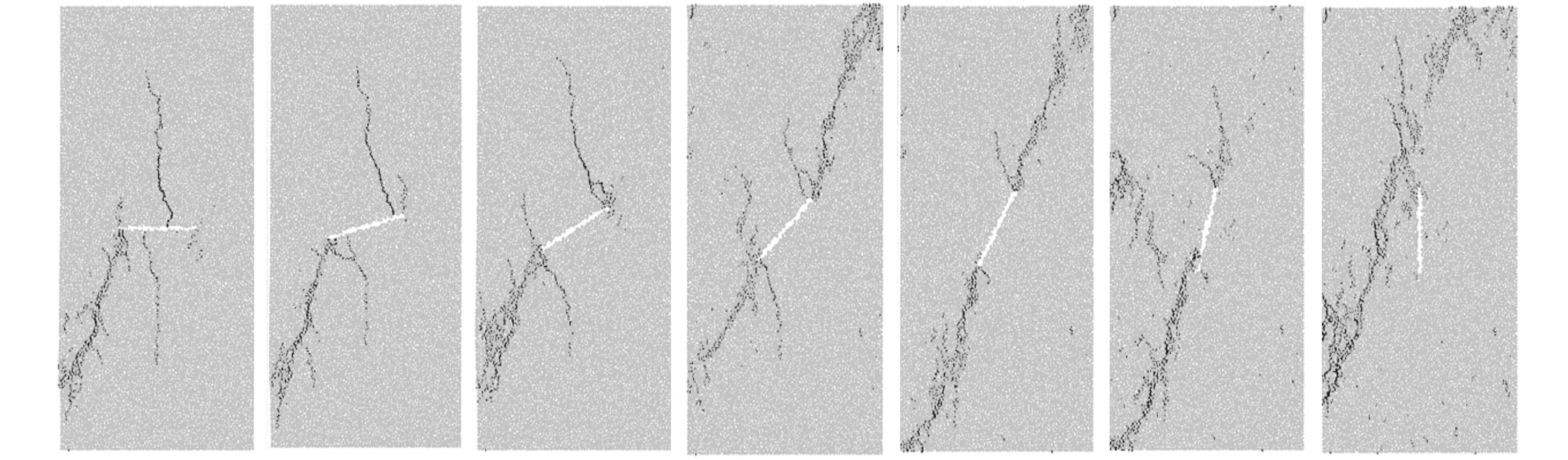
(a) α=0° (b) α=15° (c) α=30° (d) α=45° (e) α=60° (f) α=75° (g) α=90°图6 单轴压缩数值模拟试验不同倾角岩体裂纹扩展图
3.2 裂隙倾角对岩体强度的影响
通过对不同倾角预制裂隙岩体进行单轴压缩数值模拟试验,得到了图7所示的不同倾角裂隙岩体和完整岩体的应力-应变曲线图、裂纹数目-应变曲线图以及图8所示的岩体单轴抗压强度-裂隙倾角曲线图。
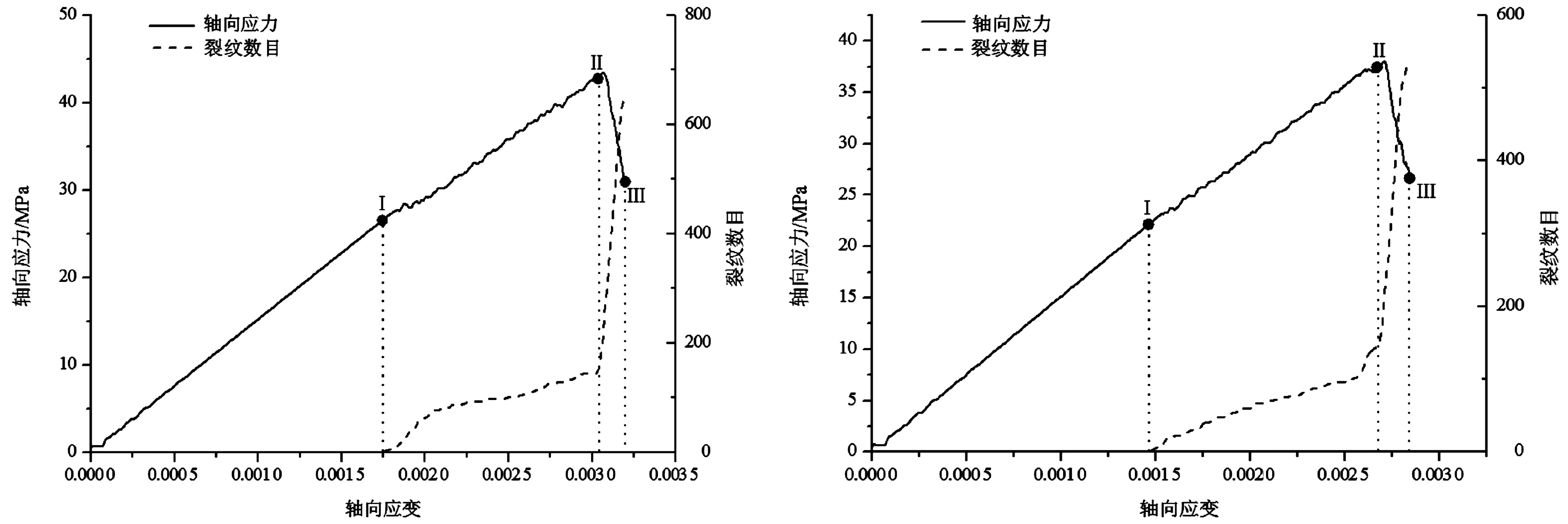
(a) α=0° (b) α=15°

(c) α=30° (d) α=45°

(e) α=60° (f) α=75°

(g) α=90° (h) 完整岩石图7 不同倾角裂隙岩体的应力-应变曲线和裂纹数目-应变曲线图
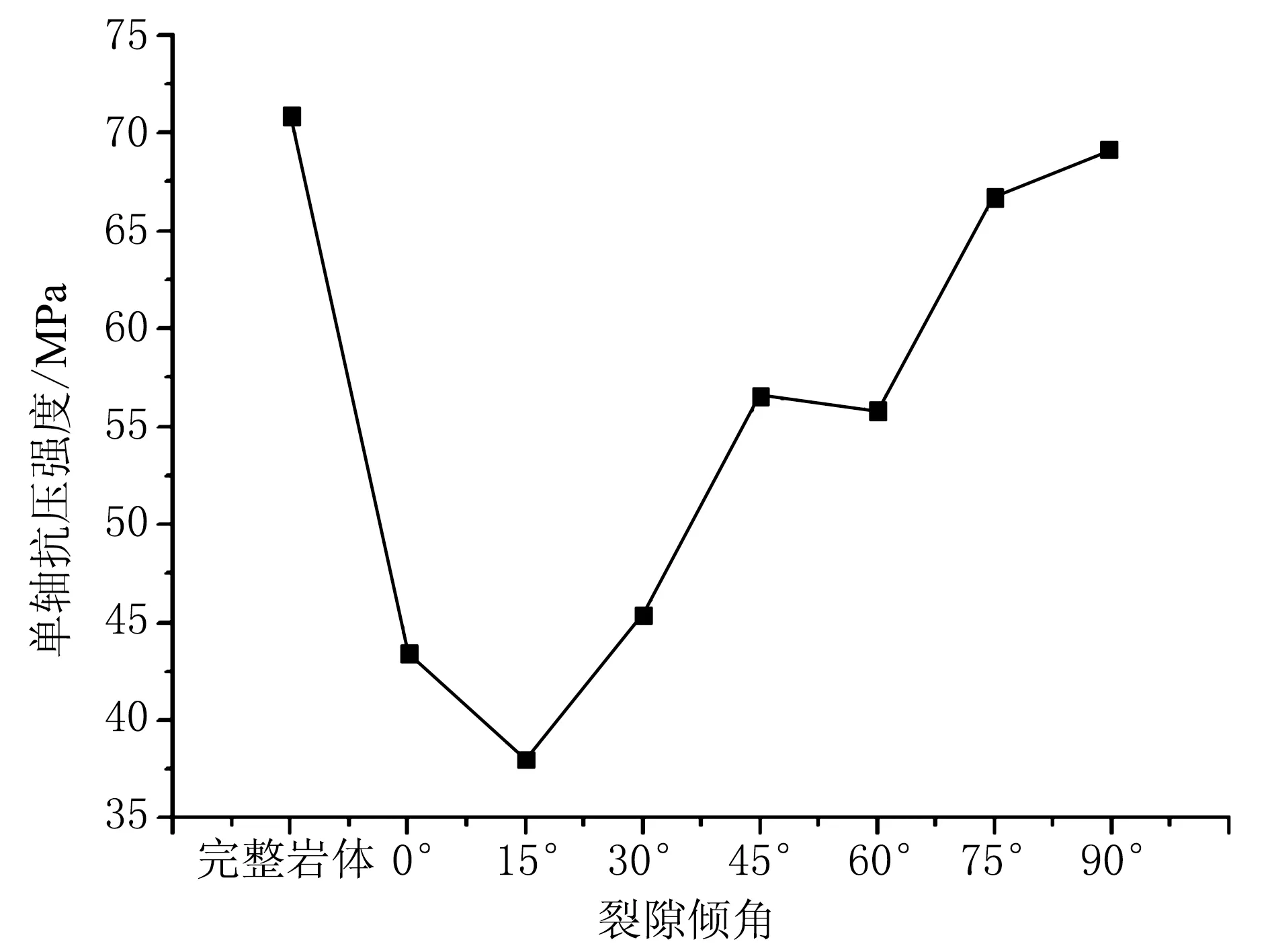
图8 岩体单轴抗压强度-裂隙倾角曲线图
从图7、图8可以看出,裂隙的存在使得岩体的抗压强度受到削弱,岩体裂隙角度不同,其抗压强度降低的幅度也不同。当裂隙的倾角为15°时,岩体的抗压强度受到的削弱最大,其强度只能达到完整岩体的50%左右;当裂隙的倾角为45°、60°时,其抗压强度几乎相同;当裂隙倾角为90°时,岩体的抗压强度降幅最小,其强度与完整岩体几乎没有差别。岩体抗压强度到达峰值之后的突变,也与岩体脆性材料的性质表现一致。结合岩体的受力状况以及裂纹的发育情况可以得出,不同倾角预制裂隙岩体在单轴压缩破坏过程中大致经历了3个阶段。
(1) 弹性变形阶段(初始-Ⅰ)。这个阶段发生时,试样内部颗粒在受压之后变得密实,这时岩体的应力与应变为线性关系。此阶段没有裂纹产生,模型在此阶段可以看成是理想弹性物质。
(2) 岩体破坏前裂纹稳定扩展阶段(Ⅰ-Ⅱ)。在此阶段,应力-应变曲线表现为非线性式增长,在端点处集中的应力超过临界值,微裂纹开始产生,但是此阶段产生的裂纹少,主要产生张拉破坏裂纹。随着荷载的增加,裂纹慢慢扩展,但此时的岩体还算稳定。
(3) 岩体失稳阶段(Ⅱ-Ⅲ)。当裂隙岩体所受的应力超过峰值后,其抗压强度急剧降低,与此同时大量的微裂纹随之产生,从而导致裂隙岩体的失稳破坏。该阶段剪切破坏的裂纹数量虽然增加了一些,但相较张拉破坏裂纹还是较少,说明裂隙岩体在单轴压缩破坏过程中张拉破坏占据主导地位。
从图7、图8还可以看出,不同倾角预制裂隙岩体的应力-应变曲线变化基本一致。随着裂隙倾角度数的增加,岩体的抗压强度也是随之增加,越来越接近于完整岩体的强度值。
4 结语
本文利用二维颗粒流程序(PFC2D),对不同倾角裂隙岩体试样进行单轴压缩数值模拟,研究了不同倾角裂隙岩体的抗压强度变化规律、破坏形式以及裂纹扩展的路径,得到如下结论:不同倾角预制裂隙岩体的破坏模式略有不同,当预制裂隙倾角为90°时,裂纹的扩展几乎与完整岩体一致,破坏形态也几乎与完整岩体相同,说明90°裂隙的存在对岩体影响最小;不同倾角预制裂隙岩体破坏过程基本一致,都会经历3个阶段,即弹性变形阶段、裂纹稳定扩展阶段、岩体失稳阶段;不同倾角预制裂隙的岩体应力-应变曲线基本一致,随着裂隙角度的增加,岩体的抗压强度也随之增加,越来越接近于完整岩体的抗压强度值。本文数值模拟分析从细观角度展示了裂纹扩展过程,为进一步探索地下工程中裂隙岩体失稳破坏规律提供了参考。

