智能喷胶机器人的姿态控制与轨迹规划

吴拱星

(黎明职业大学 智能制造工程学院， 福建 泉州 362000)

目前，我国制鞋业自动化水平较低，在喷胶流程上，只有少数企业的个别工序使用了自动化装备，大部分工序仍依靠工人手工完成，生产效率较低。为促进制鞋业健康发展，急需研发自动化智能喷胶生产线。为此，本文针对智能喷胶机器人开发的关键技术，重点研究机器人的姿态控制与轨迹规划。

在机器人焊接、喷涂、打磨抛光等工业领域，机械臂末端工具的姿态影响其作业结果。工业机器人的作业对象包含很多不规则的曲面，不规则曲面的路径规划对机器人的作业过程有很大的影响。在鞋底喷胶工序中，鞋底为各种型号的不规则曲面，机器人喷胶路径需根据不同型号的鞋底进行自适应规划。因此，喷胶路径规划是整个工序的重点。目前空间机械臂的路径规划问题多集中于机械臂的避障规划，而关于末端工具姿态控制的路径规划研究较少。KIM提出一种基于鞋底和鞋帮三维扫描数据来自动提取喷胶轨迹的方法，该方法操作复杂，很难有效地控制精度[1]。KWON等提出一种基于鞋底轮廓线生成喷胶轨迹的方法，它能根据给定的鞋底轮廓线自动生成喷胶轨迹，但提取的轨迹是平面曲线，通用性差，不能满足个性化制鞋的要求[2]。武传宇、WANG等根据线结构光三维测量原理，获取鞋帮底面的曲面信息，并算出了喷胶轨迹，但该方法并未提及喷胶姿态的控制问题[3-4]。

点云配准是指通过扫描采样获得两组有重复区域或形状相近的点云数据，采用合适的坐标变换使两组点云数据尽量在空间上重合，从而合并在一个统一的坐标系下。用于点云配准的主要方法有最近点迭代法(Iterative Closest Point，ICP )、正态分布法(Normal Distributions Transform，NDT)、奇异矩阵法(Singular Value Decomposition，SVD)和极大似然法，其中ICP是最常用的点云配准方法[5-6]。实际上，每种方法都有其局限性，比如ICP受限于其初始位置，极大似然法则受限于噪声点等，于是针对不同应用场景产生了多种改进算法。本文以工业六轴机械臂为研究对象，结合鞋底喷胶的应用，对鞋底喷胶路径进行规划，控制机器人末端工具的姿态，实现机器人智能喷胶；通过机器视觉与点云配准技术实现鞋底、鞋面喷胶位置的自动计算。传统的配准对象都是高度重复的一对点云，配准相对容易，而本文匹配的点云对是通过线激光传感器扫描得到的鞋底和鞋面两组点云数据，点云对之间无完全重叠的部分，只是形状相似，并且点云对的初始位置是可翻转的，难以直接通过ICP进行精确配准。目前这种配准对象的配准方法相对罕见。为了使点云对尽可能重叠匹配，本文先采用SVD快速得到点云对的粗匹配结果，再利用ICP精确匹配点云对，使得点云对统一到同一坐标系下；同时，针对实际生产中存在的特殊情况，拟利用Bezier曲线拟合方法对鞋底点云的轮廓线进行局部变形，以期顺利实现智能喷胶，达到理想的喷胶效果。

1 智能喷胶机器人的控制流程

机器人智能喷胶系统如图1所示。它主要包括机器人、线激光传感器、胶枪及工控机等。智能喷胶机器人能够根据不同的鞋型进行自适应控制，完成鞋面和鞋底的喷胶任务，具体包括鞋底喷胶、鞋底鞋面匹配喷胶。其控制流程如图2所示。系统通过线激光传感器扫描鞋底，得到鞋底曲面，对数据处理后进行鞋底喷胶路径规划；在完成鞋底路径规划的条件下，实现鞋底鞋面的点云数据匹配，从而在工控机上生成控制程序，导入机器人，控制机械臂完成喷胶任务。

图1 机器人智能喷胶系统

图2 智能喷胶机器人的控制流程

2 鞋底喷胶的轨迹规划

由线激光传感器得到的鞋底曲面信息是由一组三维点云数据构成的。在鞋底喷胶轨迹规划中，将鞋底三维点云数据投射到XOY平面上，提取鞋底最外圈轮廓，并对轮廓曲线进行偏置处理，生成喷胶轨迹曲线。XOY平面的鞋底轮廓曲线为：

r(u)=(x(u),y(u))

(1)

偏置处理后曲线为：

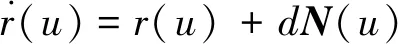
(2)

式中：d为偏置(d>0，表示沿着曲线r(u)的外法线方向移动d个单位；d<0 ，表示沿着曲线r(u)的内法线方向移动d个单位)；N(u) 为单位法向量，即

(3)

设置偏置的距离，对轮廓曲线上的每个数据点及两个相邻点进行分段处理，可近似求得曲线上每个点对应的法线。根据式(2)和式(3)可得对应偏置的鞋底喷胶轨迹。

3 机器人关节的运动学逆解

鞋底是不规则的曲面，鞋底的喷胶作业若采用普通的路径规划方法，则可能产生喷胶不完整、不均匀的现象。在鞋底喷胶中，使末端工具的姿态跟随喷胶轨迹曲线斜率的改变而改变，能够保证鞋底的完整均匀喷胶。这就需要根据机器人喷胶时的姿态对机器人关节进行控制，通过运动学逆解得到机器人关节转动的角度。

作为本文研究对象的工业机器人为安川Motoman-MH5F机械臂。其连杆坐标系如图3所示。机器人以六自由度连杆相串联。具体来说，关节1绕基础坐标系{0}的Z轴转动，关节2、3、5绕X轴转动，关节4、6绕Y轴转动。

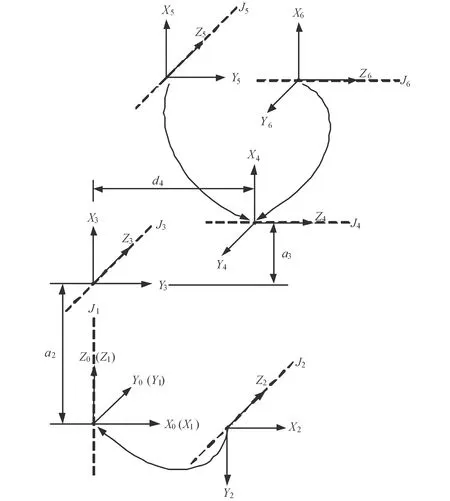
图3 安川Motoman-MH5F机器臂的连杆坐标系

根据鞋底喷胶轨迹曲线及胶枪的姿态，结合机器人运动学方程逆解确定变换矩阵。该变换矩阵为：

(4)

相应地，可得到机器人关节1到关节6转过的角度θ1至θ6。

采用二阶多项式拟合方法，对鞋底喷胶轨迹曲线进行平滑处理，先后以4圈喷胶轨迹为对象，将每圈轨迹曲线近似十等分，得到的喷胶轨迹曲线如图4所示。

图4 平滑处理后的喷胶轨迹曲线

4 鞋底鞋面的匹配算法

运用ICP匹配点云的关键是点云对的位置初始化。当点云对的初始位置相差较大时，匹配效果往往较差[7]。在鞋面喷胶需要匹配的原始点云对中，鞋底是17 027×3(像素)的双精度数据类型的矩阵，鞋面是18 173×3(像素)的双精度数据类型的矩阵。原始点云对如图5所示。

图5 原始点云对

运用ICP实现精确配准前需要对点云对的位置进行初始化。利用SVD可以消除点云对的旋转错位和平移错位，初步求出点云对的旋转矩阵和平移向量，完成位置初始化，得到粗匹配结果。

设A∈Rm×n(矩阵R包含m行、n列)，ATA的特征值的非负平方根称作A的奇异值；A的奇异值的全体记作σ(A)。当A为复矩阵Cm×n(矩阵C包含m行、n列)时，只需将ATA改为AHA，上述定义即仍然成立。根据奇异值分解定理，设A∈Rm×n，则必存在正交矩阵U=[u1,…,um]∈Rm×m和V=[v1,…,vn]∈Rn×n，使得：

(5)

式中，∑r=diag(σ1，σr)(这里，σ1≥σ2≥…≥σr>0)，为矩阵A的全部非零奇异值。

在现代科学计算中，SVD的应用广泛，如用于确定投影算子。假设矩阵A∈Rm×m的秩为r，并将式(5)改写为：

A=U∑VT

(6)

粗匹配的旋转矩阵为：

(7)

粗匹配的平移向量为：

T=[-84,823 9 421.686 6 109.538 3]

(8)

点云对粗匹配的结果如图6所示。

图6 点云对粗匹配结果

5 ICP精确匹配

点云对的SVD配准只是实现点云的大致匹配，并未达到精确配准的要求，但它完成了点云的位置初始化工作。因此，对点云对进行SVD配准后，可进一步利用ICP对点云进行精确配准。ICP是一种基于自由形态曲面的配准方法。其基本思想是：首先根据原始模型上的点集，在目标模型上找到对应的点集，即找到初始匹配点，以对应点间距离的平方和最小为原则，建立目标方程；然后，根据最小二乘原理求取转换参数，即可完成对应点的精确匹配。其数学表示为：已知两个对应点集合X′={x1,x2，…，xn}和P′={p1,p2，…，pn}，求解旋转矩阵R′和平移向量T′，使得目标函数的值最小。

(9)

利用ICP进行15次迭代，得到的精确匹配旋转矩阵为：

(10)

精确匹配的平移向量为：

T′=[-2.789 9 14.451 4 -60.955 5]T

(11)

采用ICP精确匹配的结果如图7所示。

图7 采用ICP精确匹配的结果

通过模拟及实际测试可知，本文采用的机器人姿态控制与轨迹规划方法能够满足制鞋喷胶自动化的要求。

6 结语

以工业六轴机械臂为研究对象，对其鞋底、鞋面喷胶路径进行规划，控制机器人末端工具的姿态，实现了机器人智能喷胶。通过线激光传感器扫描得到鞋底的曲面信息，提取鞋底轮廓曲线，对其进行偏置处理，生成鞋底的喷胶轨迹，并根据鞋底的轮廓曲线对喷胶轨迹进行修正，达到了平滑曲线的效果。此外，针对鞋底鞋面拟合喷胶问题，首先采用SVD进行粗匹配，使得点云对方向一致且相互靠近，然后通过ICP实现了精确匹配。通过模拟及实际测试可知，本文采用的机器人姿态控制与轨迹规划方法能够满足制鞋喷胶自动化的要求。