2019 年高考函数经典问题聚焦

■江西省赣州中学

函数是中学数学的核心内容,是高中数学知识的一条主线,也是历年高考数学的考查重点,了解高考要求及近年来高考动态,熟悉并掌握各类函数问题的题型与解法,对于2 0 2 0年高考一轮复习备考,提高高考成绩,有着非常重要的意义。本文以2019年高考函数试题为载体,聚焦其考查方向,归纳提炼其题型和求解的通性通法,希望对同学们的备考能有所帮助。

聚焦1——函数的概念、定义域、值域

1.函数的定义域。

例1 (2019年高考江苏卷文4)函数的定义域是

解析：由题意得到关于x的不等式,解不等式可得函数的定义域。由已知得7+6xx2≥0,即x2-6x-7≤0,解得-1≤x≤7,故函数的定义域为[-1,7]。

反思：求函数的定义域,从分式分母不为零、偶次根式下被开方数非负、对数中真数大于零等出发构建不等式组求解,常常与集合的交、并、补运算联系在一起。有时还涉及复合函数的定义域,凸显整体变量观念的认识和应用。

2.利用初等函数区间上的单调性求值域。

例2 (2019年高考上海卷1 3)下列函数中,值域为[0,+∞)的是( )。

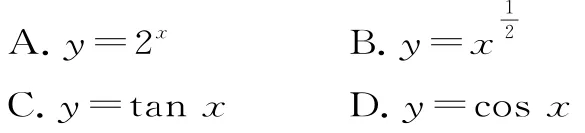
解析：依据给定的基本初等函数逐一确定值域进行判断,对于A,y=2x的值域为(0,+∞),故A错误。

对于C,y=t a nx的值域为(-∞,+∞),故C错误。

对于D,y=cosx的值域为[-1,1],故D错误。

反思：幂、指数、对数函数及三角函数构成基本的初等函数,求基本初等函数在给定区间上的值域是函数的一个重要应用,应熟练掌握基本初等函数的图像和性质。

3.利用导数研究函数的单调性进而确定最值。

例3 (2019年高考江苏卷文1 0)在平面直角坐标系x O y中,P是曲线(x＞0)上的一个动点,则点P到直线x+y=0的距离的最小值是

解析：平移直线x+y=0到与曲线y=相切的位置时,切点Q与点P的距离即为点P到直线x+y=0的最小距离。设点Q(x0,y0),则由=-1,得舍去),即切点,则切点Q到直线x+y=0的距离为,即点P到直线x+y=0的距离的最小值是4。

反思：曲线上任意一点到已知直线的最小距离,以形助数转化为曲线上过切点的切线与已知直线平行的平行线间的距离,借助导数的几何意义确定切点坐标,利用点到直线的距离公式求解,渗透了直观想象和数学运算素养。凸显数形结合和转化与化归的思想方法解题。

聚焦2——函数的图像及其变换

1.函数解析式与其图像匹配中的“函数性质和排除法”的应用。

例4 (2019年高考全国Ⅲ卷理7)函数在[-6,6]上的图像大致为图1中的( )。

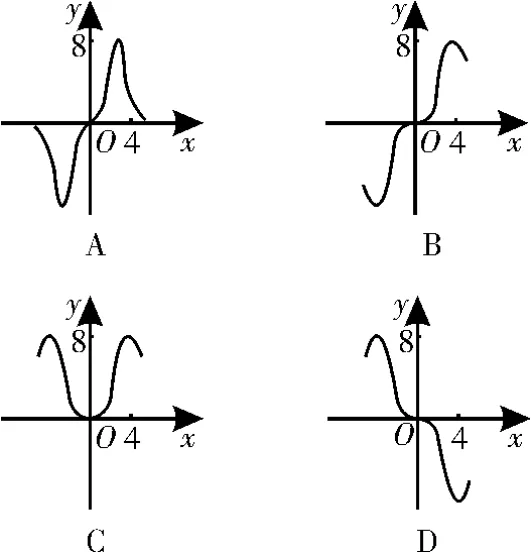
图1

解析：由分子、分母的奇偶性,易于确定函数为奇函数,由f(4)的近似值即可得出结果。设则,所以f(x)是奇函数,图像关于原点成中心对称,排除选项C。又,排除选项D。,排除选项A。故选B。

反思：本题考查函数的图像与性质,渗透了逻辑推理、直观想象和数学运算等素养。采取性质法或赋值法,利用数形结合思想解题。函数解析式与函数图像的匹配方法有:

(1)由函数的定义域,判断图像的左、右位置,由函数的值域,判断图像的上、下位置;

(2)由函数的单调性,判断图像的变化趋势;

(3)由函数的奇偶性,判断图像的对称性;

(4)由函数的周期性,判断图像的循环往复。

常常选用奇偶性和区间上的单调性,以及特殊值来寻求简捷的解题途径。

2.函数解析式与其图像匹配中的“初等函数的性质法”。

例5 (2019年高考浙江卷6)在同一直角坐标系中,函数＞0且a≠0)的图像可能是图2中的( )。

解析：通过讨论a的不同取值情况,结合指数和对数函数的图像特征来推理及验证。

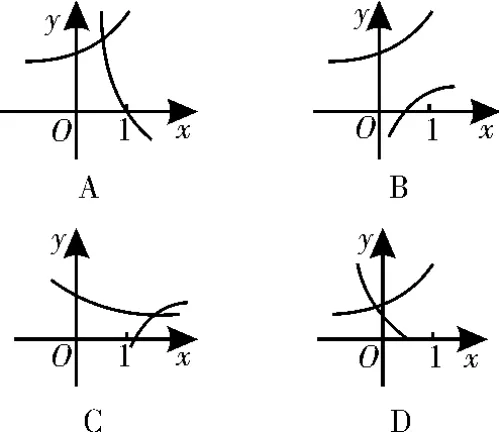
图2

当0＜a＜1时,函数y=ax过定点(0,1)且单调递减,则函数过定点(0,1)且单调递增,函数过定点且单调递减,D选项符合;当a＞1时,函数y=ax过定点(0,1)且单调递增,则函数过定点(0,1)且单调递减,函数y=过定点且单调递增,各选项均不符合。故选D。

反思：基本函数特征反映在图像的对称性和单调性,以及恒过的定点等方面,用指数和对数借助底数分类确定函数单调性和过特殊点的方法合理推理,要求熟练掌握指数、对数函数的图像和性质。

聚焦3——灵活应用函数性质进行代数式的大小比较

例6 (2019年高考全国Ⅱ卷理6)若a＞b,则( )。

解法1：直接法求解,因为a＞b,所以a-b＞0,当a-b=1时,ln(a-b)=0,故A错误;因为y=3x是增函数,所以3a＞3b,故B错误;因为幂函数y=x3是增函数,a＞b,所以a3＞b3,故C正确;取a=1,b=-2,满足a＞b,但1=|a|＜|b|=2,故D错误。

解法2：特殊值法,取a=2,b=1,满足a＞b,ln(a-b)=0,故A错误;因为9=3a＞3b=3,故B错误;取a=1,b=-2,满足a＞b,1=|a|＜|b|=2,故D错误;因为幂函数y=x3是增函数,且a＞b,所以a3＞b3,故C正确。

反思：本题主要考查对数、指数、幂函数的性质及绝对值意义,渗透了逻辑推理和运算能力素养。