基于剪式控制力矩陀螺的低轨卫星垂轨摆扫姿态控制*

曹永奎 廖育荣 倪淑燕 杨新岩

1.航天工程大学研究生院，北京101416 2.航天工程大学职业教育中心，北京 101416 3.航天工程大学电子与光学工程系，北京 101416

针对大范围区域进行持续性监测，对于环境管理、空天安全等都具有重要意义。借助卫星姿态机动来调整探测器主轴方向，通过视场拼接实现大范围探测是低轨卫星实现大面积对地观测的有效手段[1-2]。当前卫星多采用多条带成像[3]方式来满足大范围探测的需要，在这样的方式下，卫星一次过顶的时间内，部分时间必须用于卫星姿态调整[4]，缩减了实际探测时间[5]；部分研究通过扫描轨迹规划提高过顶时间利用效率[6-7]，但仍需要在成像间隙调整姿态。沿垂轨方向的扫描成像方式，能在整个过顶过程中都进行探测，但目前仅有线阵扫描方式[8]，未见星载面阵相机的垂轨摆扫应用。

垂轨摆扫方式对卫星姿态机动能力提出很高的要求。现常用的姿态执行机构有喷嘴、反作用飞轮、磁力矩器，控制力矩陀螺等。控制力矩陀螺(Control Moment Gyroscope，CMG)具有精度高、力矩大的特点[9]，是低轨成像卫星的首要选择。在使用CMGs时，当前一般采用金字塔型、四棱锥和五棱锥型安装，这类方式一般只能对称安装，且存在内部奇异，需要用特殊方式避免或逃离奇异位置[10-12]。任务要求卫星按照预定轨迹快速姿态机动，需要执行机构提供大力矩输出。剪式CMGs在输出上具有操纵律简单、力矩解耦合[13-15]的特点，本文使用剪式CMGs作为执行机构。

针对卫星姿态垂轨摆扫，使用三轴非对称安装的剪式CMGs作为执行机构设计姿态控制系统，简化陀螺框架角操纵律，避免系统出现内部奇异，减小了执行机构质量，实现卫星姿态的快速摆动。

1 垂轨摆扫大范围探测过程

如图1所示，利用低轨成像卫星对于目标区域进行大范围扫描探测，需要利用成像卫星的姿态控制能力，调整卫星成像载荷对地指向，实现比传统低轨探测方式更大的检测范围。

图1 使用垂轨摆扫进行大范围探测

卫星到达目标区域上空，从区域的一端开始探测，完成后调整视场垂直轨道移动，进行下一次探测，使2次探测视场之间能够拼接成一个更大的视场，如此反复直到探测视场移至目标区域另一端，形成一个垂直轨道的带状区域；之后又反向重复此过程。如此反复直至覆盖整个区域，在此过程需要卫星进行精准的三轴姿态机动。

实际摆扫中为简化姿态控制，可以只进行滚动角调整进行垂轨摆扫，沿轨方向可由卫星的轨道运动进行推进。

如图2所示，探测中2个视场之间有重复区域，这能保证拼接效果以及实现多次探测，提高对于微小目标或弱强度目标的监测概率。需要注意的是，实际运动中由于垂轨运动为变速，因此指向轨迹不是简单折线，而是曲线，但只要前后2个周期的探测视场在沿轨方向刚好实现拼接，对于图像拼接就没有影响。

图2 垂轨摆扫探测的视场拼接

本文设定相关任务参数如下：

h=500km，R=6400km
s=a×b=100×100km2
S=l×w=1000×1000km2

其中，h为轨道高度；R为地球半径；s为探测器单幅探测面积；a为沿轨幅宽；b为垂轨幅宽；S为探测目标区域面积；为l表示区域沿轨长度；w表示区域垂轨宽度。

在此设定下，任务总时间为：

(1)

式中，GE=3.986×1014m3/s2为地球引力常数， 探测推进长度为akm时，(摆扫一个来回)时间为：

(2)

在一次任务中，需要进行10次垂轨摆扫来完成对整个目标区域的探测，并且重复区域的大小不会影响摆扫周期，可以通过控制探测器探测帧率来控制重复率，即重复率不会改变对于卫星姿态控制的需求。

2 垂轨摆扫轨迹设计

综合考虑卫星成本以及性能要求，卫星摆扫时的姿态变化应按照特定轨迹进行，从而保证视场拼接。本文所述摆扫运动，绕着星体的横滚角转动，因此进行轨迹设计的时候，主要考虑卫星横滚角的机动，默认卫星的另外2个姿态角保持不变(仅在空间干扰力矩作用下存在微小变化)。

2.1 恒角加速度姿态运动

恒角加速度运动即是保持角加速度值为恒定的运动，是较简单的转动形式。在卫星执行机构的最大力矩确定时，恒角加速度运动是一种时间最优的姿态机动轨迹。在一个摆扫周期内，其各个运动学参量的关系如下：

(3)

(4)

(5)

进行这样的恒角加速度的姿态机动时，角加速度存在突变，对于执行机构要求高，并且会导致卫星的挠性振动。

2.2 正弦角加速度姿态运动

如图3所示，正弦加速度运动的加速度曲线满足正弦关系。正弦加速度轨迹平滑，对于星体和控制器件之间没有力和力矩的突变，有利于卫星的稳定运行，尤其对于挠性卫星，正弦加速度运动能够有效避免卫星振动。

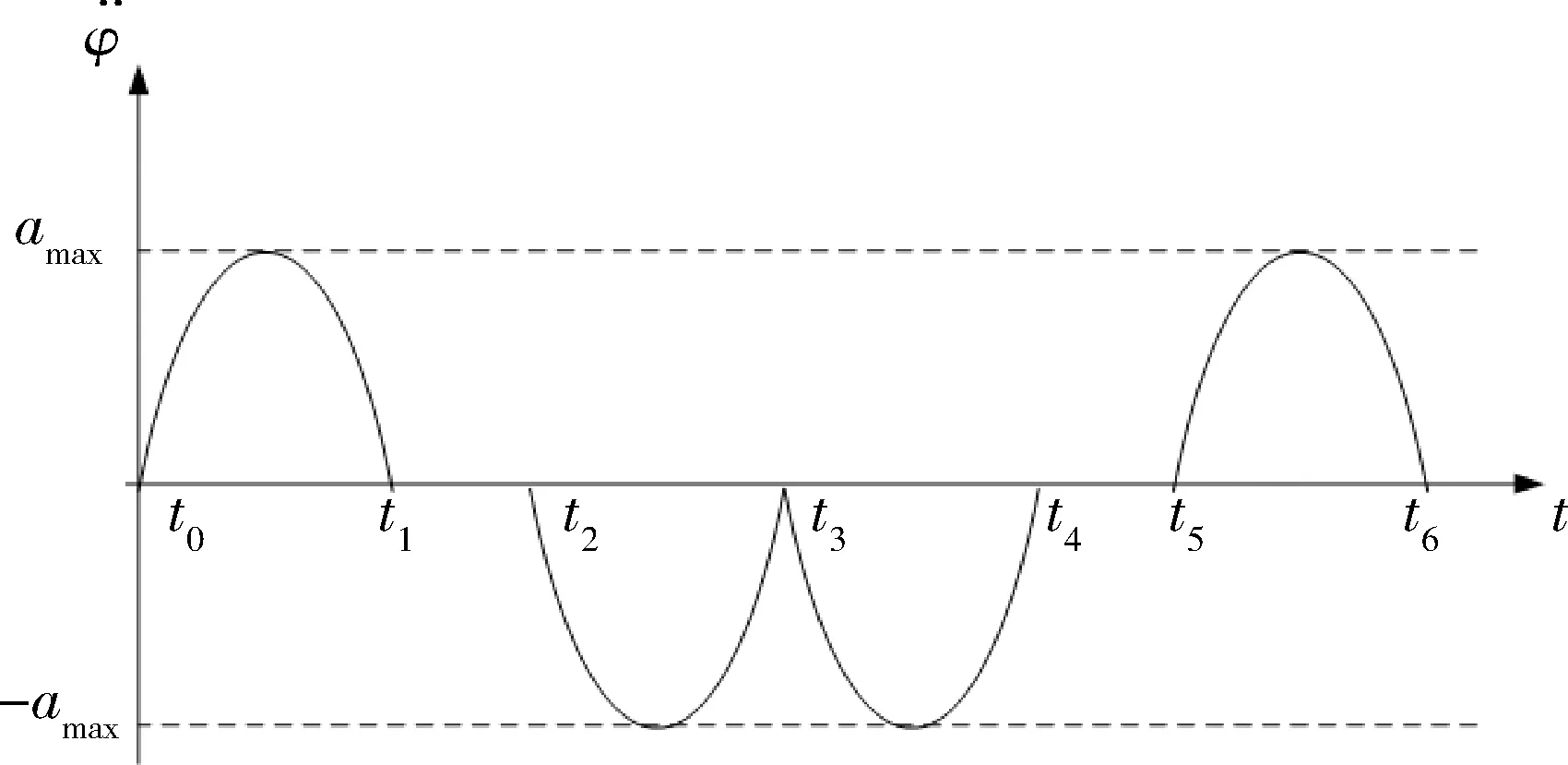
图3 摆扫中正弦加速度运动加速度曲线

图3所示为正弦加速度运动1个周期内的角加速度变化曲线，其中，t0～t6为1个周期T；t0和t3时刻卫星的滚动角分别为2个极限值。由于t0～t3，t3～t6两时段运动特性一致，仅仅是方向相反，因此对t0～t3时段进行分析，并且有t3-t0=T/2。图中加速段与减速段经历时间相同，即是：t1-t0=t3-t2。

如图3所示，t0～t3各个阶段的角加速度为：

(6)

进一步得角速度和角度关系为：

(7)

(8)

3 基于剪式CMG的卫星姿态控制

3.1 基于四元数表示的卫星姿态控制

用单位四元数表示卫星的姿态动力学，具有计算量小、避免奇异等优点；通过姿态四元数研究大角度机动问题较为方便。用四元数表示卫星姿态运动学的表达式为：

(9)

其中：

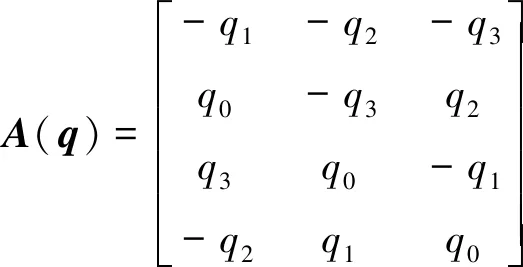
根据欧拉定理，卫星转动角动量与力矩之间的关系为：

(10)

其中,H为星体角动量;u为控制力矩;Td=[Tx,Ty,Tz]T为卫星受到的干扰力矩总和。干扰力矩来源主要有重力梯度力矩、地磁力矩和太阳光压力矩等，为简化计算，本文用1个零均值的高斯分布干扰力矩进行等效。

本文采用原理简单、应用广泛且效果稳定的PD控制器进行姿态控制。基于误差四元数的PD控制器原理为：

Tu=-KpJqev-KdJω+ω×Jω

(11)

转动惯量矩阵J为一个3×3方阵，由卫星自身质量分布决定，一般可以将其取为对角阵；同样一般取Kp=diag(kp1,kp2,kp3)为对角阵，Kd=diag(kd1,kd2,kd3)，并且Kpi和Kdi均为正数。式中qev为误差四元数的矢量部分，误差四元数由当前姿态四元数q和期望姿态四元数qd计算而得。

3.2 剪式控制力矩陀螺操纵律

单框架控制力矩陀螺的示意图如图4。

图4 单框架控制力矩陀螺示意图

(12)

将一对CMGs进行剪式安装示意图如图5，2个CMG固连在同一个支架上，初始状态时2个陀螺的角动量共线但方向相反。在输出力矩时，2个CMG框架角之间始终保持关系δ1+δ2=π。

图5 剪式安装的CMGs示意图

图6 剪式控制力拒陀螺力矩输出

图6为CMGs输出示意图，其中δi表示框架角度值，Δhi为角陀螺角动量变化量。由于框架角驱动轴平行于y轴，因此陀螺角动量在xoz平面变化。分析得：

(13)

其中,H1为陀螺转子角动量大小;i和j分别为x，z轴的单位矢量。由于δ1+δ2=π，则：

(14)

可以看出剪式CMG将z方向的力矩输出耦合

抵消了，最终的力矩输出沿x轴方向。

由于卫星需要三轴稳定控制，因此需要在三轴都装上剪式控制力矩陀螺，共需6个控制力拒陀螺。将6个控制力矩陀螺的框架角表示为δi，i=1,2…,6；其中δ1和δ2的变化输出x轴力矩，δ3和δ4的变化输出y轴力矩，δ5和δ6的变化输出z轴力矩。类比式(11)，得到如下关系：

(15)

由于剪式控制力矩陀螺满足约束：h3=h4=H2,h5=h6=H3，将CMG系统的总角动量变化率和框架角速度之间的关系表示为式(16)：为保证矩阵的求逆，附加约束条件δ1+δ2=δ3+δ4=δ5+δ6=π，将雅克比矩阵写成方阵形式，获得关系如式(17)：

(16)

(17)

4 卫星摆扫运动控制仿真

由式(2)得摆扫时一个周期为T=14.2s，系统刷新速率为Δt=0.05s，卫星的转动惯量为：

PD控制参数为

干扰力矩Td服从均值为0、标准差为0.05的正态分布。由于实际中横滚角是主要机动方向，对于CMGs力矩输出要求较大；而俯仰角和偏航角上仅需要调节由误差引起的姿态扰动，对于CMGs力矩输出要求小，因此选用更小输出的CMG，能够减小执行器质量，降低系统功耗。

仿真时设定CMG转子角动量为：

H1=1.3kg·m2/s
H2=H3=0.25kg·m2/s。

取2个摆扫周期作为仿真对象，分别对于恒角加速度运动和正弦角加速度运动时的卫星姿态运动参数、CMGs输出力矩以及框架角速度变化情况进行分析。

a)按照恒角加速度运动进行垂轨摆扫的matlab仿真结果如图7～10所示

图7 恒角加速度垂轨摆扫欧拉角变化情况

图8 恒角加速度垂轨摆扫欧拉角误差

图9 恒角加速度垂轨摆扫控制力拒

图10 恒角加速度垂轨摆扫陀螺框架角

在选定的仿真参数下，滚动轴姿态误差最大值为1.28°。对于x轴向控制力拒，其绝对值均值为0.61N，其最大值为0.91Nm；y轴向控制力矩绝对值均值为0.051N，最大值为0.19N；z轴向控制力矩绝对值均值为0.053N，最大值为0.16N。x轴上的控制力矩陀螺框架角工作空间为-57.9°～57.1°；y轴上的控制力矩陀螺框架角工作空间为-36.5°～38.6°；z轴上的控制力矩陀螺框架角工作空间为-38.7°～37.9°。

b)按照正弦角加速度转动进行垂轨摆扫的matlab仿真所得结果如图11～13所示。

图11 正弦角加速度垂轨摆扫欧拉角误差

图12 正弦角加速度垂轨摆扫欧拉角误差

图13 正弦角加速度垂轨摆扫控制力矩变化情况

图14 正弦角加速度垂轨摆扫陀螺框架角

在选定的仿真参数下，滚动轴姿态误差最大值为2.12°。对于x轴向控制力拒，其绝对值均值为0.62N，其最大值为1.13Nm；y轴向控制力矩绝对值均值为0.052N，最大值为0.19N；z轴向控制力矩绝对值均值为0.054N，最大值为0.22N。x轴上的控制力矩陀螺框架角工作空间为-59.2°～58.3°；y轴上的控制力矩陀螺框架角工作空间为-37.5°～36.9°；z轴上的控制力矩陀螺框架角工作空间为-38.2°～34.2°。

正弦角加速度姿态机动的优势在于能够有效减小卫星振动，但是从仿真结果来看，正弦角加速度姿态机动的角度误差要大于恒角加速度姿态机动的误差，并且CMG的最大力矩输出要求也更大。因此在对振动抑制没有特殊需求时，选择恒角加速姿态机动效果更好。

5 结论

针对大范围持续监测任务，设计了基于剪式CMGs低轨卫星垂轨摆扫探测姿态控制系统。仿真结果表明选用的剪式控制力矩陀螺框架角在允许范围内变化，摆扫期间没有出现奇异，控制系统能够实现对预定轨迹的稳定跟踪，完成大范围探测任务。