高速取纸机构主凸轮廓线设计及运动分析
杨奔奔 曹巨江 刘言松 杨 坤
(陕西科技大学机电工程学院,陕西 西安 710021)
在中国传统文化中,食品作为一种走亲访友的礼物已流传千年之久,如茶、酒、点心等。作为礼物其精美的包装是必不可少的。因此,食品包装工业已成为现代食品生产工业体系中最重要的一部分,其中纸质包装应用最为广泛[1]。中国食品包装机械的发展可追溯至20世纪,如香烟的包装设备[2]。高速取纸机构可用于食品包装过程中将食品外包装(包装纸、纸盒等)从整摞堆积的状态转为单个排列的状态。中国学者对取纸机构的研究经历了早期的摆动式[3]到现在回转式的过程。摆动式在高速运转下会产生较大的震动,影响整个机器的稳定性;回转式能较好地平衡惯性力,在高速取纸机构的研究中被广泛关注。
李龙等[4-5]在分析了取盒机构的运动轨迹后,提出了一种四头凸轮—连杆的串联机构,可达到很好的取盒目的。王宏祥等[6]通过研究四头行星轮系取盒机构的运动规律建立数学模型,确定了影响其运动的关键参数,完成了对机构的优化设计。童俊华等[7]设计了一种以椭圆—圆齿轮为传动机构的行星轮系取盒机构,该机构与圆齿轮行星系取盒机构相比,其运动特性进一步得到了优化。但目前研究或是因为机构自身特点或是刚性较差等原因,只能在较低转速下平稳运行。
在前人研究的基础上,研究提出了一种凸轮—平行四边形串联的组合机构,并通过对凸轮廓线进行设计和分析,分析基圆半径和升程与回程的运动角对运动特性的影响,以期为后续高速取纸机构的优化设计提供理论指导。
1 双凸轮—平行四边形机构
为实现吸头较为复杂的运动轨迹,采用双凸轮和平行四边形机构(吸头装在一个连杆上)的组合机构,如图1所示。

1. 吸头 2. 从动摆杆 3. 平行四边形机构机架 4. 铰链A 5. 铰链B 6. 主动摆杆 7. 副凸轮 8. 转盘 9. 主凸轮 10. 纸仓
图1 机构原理简图
Figure 1 Schematic diagram of the mechanism
在上述机构中,双凸轮与机架固连,平行四边形机构机架3的铰接端A的运动轨迹由主凸轮9的廓线确定,另一端B铰接在转盘上,由转盘带动杆机构绕凸轮回转中心O转动,吸纸过程中通过主凸轮调整杆机构机架3姿态使得吸头1在取纸时与纸架保持平行,通过副凸轮7控制摆杆转动使吸头1在取纸过程切向绝对速度为0,在法向实现伸出、缩回保证能顺利取纸并退出。取纸过程可分为3个阶段:升程阶段、取纸阶段、回程阶段,如图2所示。
(1) 升程阶段:将铰链A 4送到指定位置,使其在下一阶段能更好地实现吸头的平行状态,该阶段通过主凸轮9廓线调整平行四边形机构机架3的姿态使吸头1与纸仓10平行。
(2) 取纸阶段:当吸头1转到取纸位置时,通过副凸轮7使主动摆杆6逆时针摆动,调整吸头1的位置使其到达纸仓,并停留一定时间,以保证成功取到纸。

图2 取纸过程Figure 2 Process of paper picking
(3) 回程阶段:吸头1取纸后,主动摆杆6在这一阶段法向的前伸动作已由最远处开始缩回,但仍与纸仓10平行退出一段距离后再转动退出取纸区域。
2 主凸轮廓线设计
主凸轮用以调整四杆机构中吸头1的姿态,以避免吸纸时吸头与纸盒间出现缝隙从而产生漏气、不能取纸的现象。
2.1 取纸过程吸头姿态分析
从图2可以看出,吸头的平行状态是从吸纸前吸头前伸开始,到取纸、吸头退回,且一直持续到退出了一定距离后结束。因此要求通过主凸轮廓线变化使得平行四边形机构的机架能在某个位置进入与料仓平行状态,且保持一定时间。
2.2 凸轮廓线设计
凸轮廓线设计的初始参数如表1所示。

表1 初始设计参数Table 1 Initial design parameters
为保证在吸纸阶段吸头保持与纸仓平行,铰接点A运动的轨迹与铰接点B轨迹半径相同,为平移一个连杆长度的圆弧。如图3所示,转盘半径R,平行四边形机构的机架长度L,β所对应圆弧为铰链B走过轨迹,α所对应圆弧为铰链A走过轨迹,该段方程为:
(1)
2.2.1 升程段凸轮廓线设计 高速运动下,为实现机构平稳运动,必须保证加速度曲线光滑[8]。高阶多项式运动规律通用性强,并能满足条件[9-11],因此本文采用七次多项式对凸轮廓线的升程段和回程段进行设计。
升程段四杆机构机架摆动角度变化如图4所示,该段摆动角度随凸轮转角变化方程为:
θ=c7φ7+c6φ6+c5φ5+c4φ4+c3φ3+c2φ2+c1φ+c0。
(2)

图3 平行段凸轮廓线Figure 3 Cam profile in parallel stage
代入边界条件:
(3)
φt=φt1-φt0+δt,
(4)
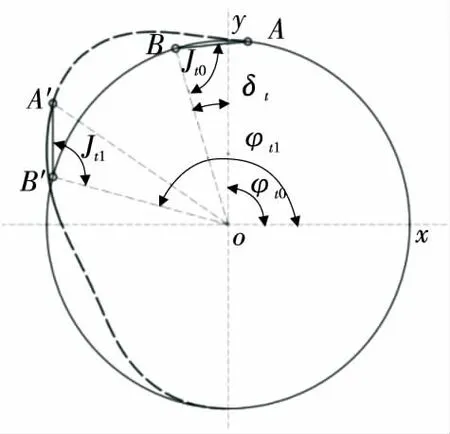
图4 升程段平行四边形机构机架摆动变化Figure 4 Variation of the frame swing of the paralle- logram mechanism of the lift section
式中:
δt——升程期凸轮转动角修正量,(°)。
当B在y轴右侧时,δt取正;当B在y轴左侧时,δt取负;当B在y轴上时,δt=0。
可得出升程段摆角变化规律为:
θ=c7φt7+c6φt6+c5φt5+c4φt4,
(5)
式中:
φt——升程段的推程角,(°)。
升程段运动过程中,铰链B轨迹方程为:
(6)
升程段凸轮廓线方程即为铰链A轨迹方程:
(7)
式中:
γt——平行四边形机架(AB)与x轴正向夹角,(°)。
γt=Jt0+θt+φt-π/2-δt。
(8)
2.2.2 回程段凸轮廓线设计 为计算方便,回程段采用反向求凸轮廓线方法。如图5所示,凸轮转角起点B'终点B,由B'向B反向计算。
回程边界条件:
(9)
φh=|φh1|-|φh0|+δh。
(10)
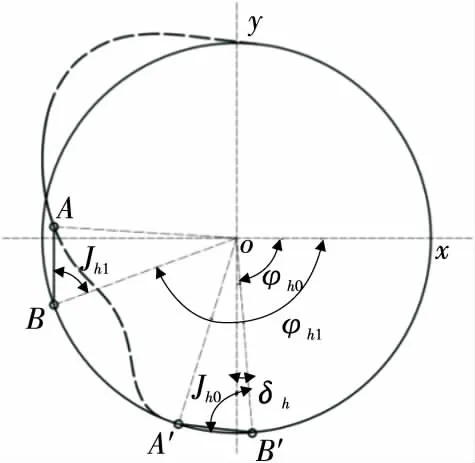
图5 回程段轨迹Figure 5 Return path track
将式(9)代入式(2)可得回程段平行四边形机构机架摆动角度随凸轮转角变化规律方程为:
θh=ch7φ7+ch6φ6+ch5φ5+ch4φ4,
(11)
式中:
δh——回程期凸轮转动角修正量,(°)。
当B'在y轴右侧时,δh取正;当B'在y轴左侧时,δh取负;当B'在y轴上时,δh=0。
回程段铰链B轨迹方程为:
(12)
回程段凸轮廓线方程为:
(13)
式中:
γh——平行四边形机架(AB)与x轴正向夹角,(°)。
γh=Jh0+θh+φh-π/2-δh。
(14)
2.3 压力角验算及分析
凸轮机构的压力角可按式(15)计算。
(15)
式中:
KQt/h——升/回程在该点凸轮廓线切线的斜率;
KLt/h——升/回程在该点平行四边形机架AB的斜率;
α'——该点处从动件压力角大小。
将式(6)、(7)、(12)、(13)代入式(15)即可得凸轮上某一点压力角的值,对式(5)、(11)分别求二阶导即可得升程段和回程段角加速度变化方程。通过对方程进行分析可知:机架AB的长度L和转盘的半径R一定时,基圆半径Rj变化范围为R-L~R+L。随着基圆半径的增加,升程段角加速度最大值会降低,但回程段角加速度最大值会增加;随着凸轮转动角的增加,升程段和回程段角加速度最大值会减小;随着基圆半径的增加,升程段压力角会增加,但并不明显,而回程段压力角增加较为明显,但其压力角最大值始终小于升程段的;随着凸轮转动角增加,升程段压力角会增加,而回程段会减小。
3 实例计算
3.1 理论分析
高速取纸机构中转盘半径R=200 mm,吸头安装所需长度L=80 mm,平行姿态保持区间β=30°,β0=170°,其他参数见表2。
初选Rj=200 mm、δt=0、δh=0,通过已知条件和计算公式,运用Matlab编写计算程序运行计算[12-13],得出理论凸轮廓线如图6所示。

表2 设计初始参数Table 2 Basic design parameters (°)
取转角修正角δ=0,运用Matlab编写计算程序,对升程段和回程段凸轮廓线在不同的基圆半径下,分析其压力角最大值和角加速度最大值变化,结果见图7、8。

图6 凸轮轮廓Figure 6 The cam profile

图7 不同基圆半径下最大压力角变化曲线Figure 7 The max pressure angle corresponding at different base circle radius
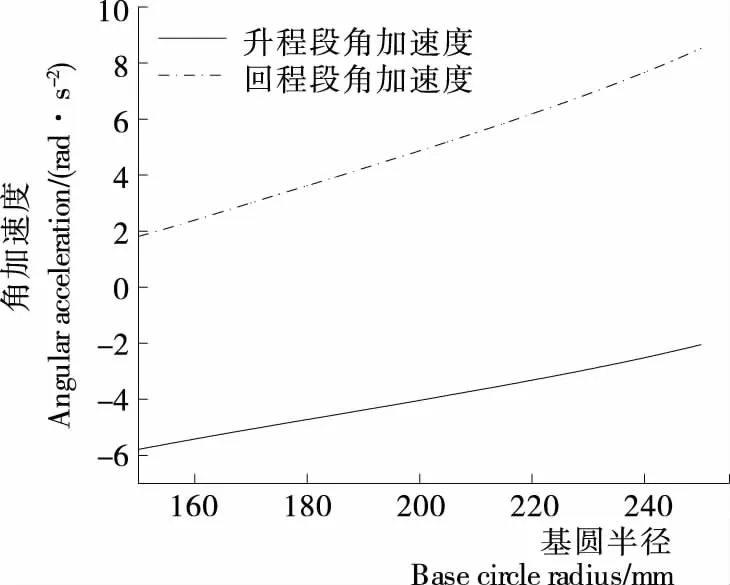
图8 不同基圆半径下最大角加速度变化曲线Figure 8 The max diagram corresponding at different base circle radius
同理,得出升程段和回程段在基圆半径为定值(取Rj=200 mm),凸轮转动角修正角δt取不同值(δt=-30°,-20°,……,30°)时,压力角和角加速度最大值变化如图9、10所示。

图9 不同转动角下最大压力角变化曲线Figure 9 The max variation of pressure angle at different rotation angles

图10 不同转角下最大角加速度变化曲线Figure 10 The max angular acceleration variation at different angles of rotation
3.2 仿真分析
取3.1中参数在UG中建立主凸轮9、平行四边形机构机架3、铰链A 4、铰链B 5和转盘8的三维模型并进行仿真,测得铰链A 4和铰链B 5在一个周期内的x轴的位移分量如图11所示,角加速度变化如图12所示。
通过对以上线图进行分析可知,本研究设计的主凸轮能满足姿态要求;基圆半径和凸轮运动角对升程段的压力角和角加速度均有较大影响,且对升程段和回程段角加速度影响结果相反;对回程段压力角和角加速度影响较小。因此,可以考虑以升程段影响为主,选择适当的基圆半径和凸轮动角,使升程段在满足条件下,角加速度最大值尽量小,回程段选择适当的凸轮运动角,使回程段角加速度最大值不超过升程段角加速度最大值。

图11 铰链A、B的x轴的位移分量Figure 11 The displacement component of the x-axis of hinges A and B

图12 角加速度变化曲线Figure 12 Angular acceleration curve
4 结论
利用七次多项式运动规律对高速取纸机构主凸轮廓线方程、压力角计算模型和角加速度方程分析可知:利用七次多项式和圆弧组合曲线实现的凸轮廓线能够满足凸轮—四杆机构高速取纸机构的姿态要求;在升程段,增加基圆半径和升程角对压力角不利,对角加速度最大值有利,满足高速取纸机构对执行件轨迹的特殊要求。但在回程段,增加基圆半径对压力角和角加速度最大值不利,而增加回程角对两者都有利,因此后续可研究通过优化方法选择合理的基圆半径和凸轮运动角。

