澳洲坚果中红外干燥机设计与试验

王教领 宋卫东 丁天航 王明友 吴今姬 周德欢 周 帆

(农业农村部南京农业机械化研究所，江苏 南京 210014)

澳洲坚果原产于澳大利亚，经过30多年的发展，中国的种植面积已超6 000 hm2，预测未来15年内，中国将成为全球最大生产国[1]。澳洲坚果仁营养丰富[2-5]，被誉为坚果之王，有较高的经济价值[6]。干制是澳洲坚果生产加工的关键环节，但由于其油脂含量高、对温度敏感且果壳坚硬，同时干燥要求将水分降到湿基含水率为1.5%的安全水分，导致目前普遍采用的传统烘房干燥需3周左右，普通热泵干燥也需要3～4 d，耗费大量能耗与人力[7-9]。普通的对流干燥因为温度与水分传递梯度方向相反，加上澳洲坚果生理特性导致干燥效率低，而辐射传热干燥一般促进温度与水分的同向传递，加速干燥过程。王云阳[10]针对上述问题开展了射频干燥技术研究，表明热风辅助射频干燥可以较好地解决干燥速率低、干燥不均匀问题。而红外干燥作为一种常见的辐射传热干燥，是通过电磁波的形式向外传递能量，其波长介于可见光和微波之间，按其波长的不同通常划分为近红外、中红外与远红外，其中中红外线辐射距离较深，适用于较厚的物料干燥，目前还未见有关澳洲坚果的红外干燥研究。

针对澳洲坚果果壳厚、水分不易扩散等问题，拟运用中红外辐射干燥技术，辅以热风干燥及风机抽湿进行调质降温，通过计算干燥曲线、水分扩散系数与活化能等探明澳洲坚果的红外干燥特性，创制中红外干燥机，以期为澳洲坚果的快速、节能干燥提供参考。

1 中红外干燥机整机结构与主要参数

1.1 结构组成与工作原理

1.1.1 结构组成 试验用中红外干燥机结构如图1所示，由进料口、加热单元、散热腔、传输系统和出料口组成，加热单元由中红外加热管、隔热板和加热腔组成，其中中红外加热管位于隔热板下方，共6个加热单位，每个加热单元设有6根中红外加热管，每根中红外管发射功率在0～1 kW内线性可调。加热腔中设有温度探头，散热腔中设置有冷却风机，环境空气从隧道两端进入，加热后被冷却风机抽到外界环境中，实现降温排湿，在保证加热温度的同时解决因加热失控造成的局部温度过高的问题[11-12]。

1.1.2 工作原理 加热开始时将澳洲坚果铺放于传输带的进料口处，打开电源，设定好加热温度、加热功率及电机转速，待温度达到设计要求时启动转速电机，开始加热，并同时开启抽湿电机不断将隧道内的湿气抽出并起到降低积温的作用。当达到加热温度时灯管灭，当低于加热温度时灯管再次打开，保证澳洲坚果的干燥温度，每次出料后根据含水率决定是否需要再次加热，如此循环直至达到干燥要求。

1.2 关键部件参数确定与选型

1.2.1 辐射器种类选型 红外辐射加热器的选型要综合考虑脱层脱落、耐高温、转换效率和稳定性等问题。基于上述因素本试验选择功率为1 kW的非涂层式碳纤维红外线石英管作为辐射体，该石英管具有热量损失小，吸收性强和转化效率高等优点。

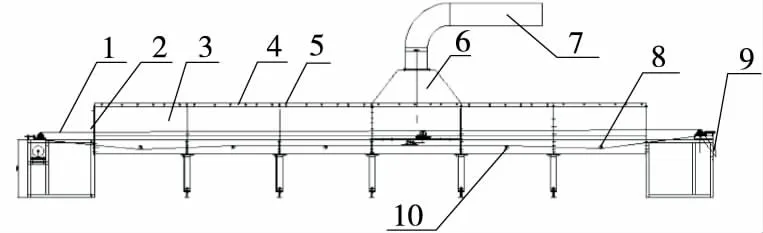
1. 输送带 2. 进料口 3. 加热腔 4. 加热板 5. 中红外加热管 6. 散热腔 7. 出风孔 8. 张紧轮 9. 出料口 10. 支撑轮

图1 中红外干燥机结构图

Figure 1 Structure of the infrared dryer

1.2.2 加热功率 根据辐射加热密度法，红外加热功率可按(1)式计算[13]：

W=E×F，

(1)

式中：

W——加热功率，kW；

E——辐射功率密度(一般取3～8，大面积薄壁工件取小值，小面积厚壁取大值)，kW/m2；

F——单位时间加热面积，m2。

根据设备的整机尺寸，加热隧道的有效面积约为9 m2，由于是大面积薄壁E取4，则W为36 kW。

1.2.3 辐射距离 设备红外加热功率为36 kW，单根红外管功率选择 1 kW，共需安装36根，每个加热单元6根，共设计6个加热单元。发射管相邻距离设计为250 mm，加热器表面与传送带距离根据经验值(一般为两相邻辐射器中心距的1.2倍)确定为300 mm。

1.2.4 主要调节因素及其控制方法 系统控制因素主要有加热腔温度、红外加热管功率与传送带转速。其中加热腔温度主要通过冷却风机不断将隧道内湿热空气抽出以实现降温，同时也促进了排湿。红外加热管功率通过电流调节器控制，传送带转速由变频电机驱动，可实现无极调速。控制系统利用PLC实现对温度和加热功率的控制。

2 材料与方法

2.1 仪器与设备

中红外干燥机：实验室自制；

电子天平：BSA224S型，广州市深华生物技术有限公司；

水分快速测定仪：MB27型，合肥祺景电子科技有限公司。

2.2 试验方法

试验地在江苏宜兴，新鲜的澳洲坚果购自广西崇左县，脱皮后邮寄到试验点后含水率约为25%。中红外干燥机的加热腔温度根据相关文献[14-15]不超过60 ℃，同时根据设备特性，设置加热腔温度为60 ℃，中红外发射管功率0.8 kW，设置好干燥温度和功率后将澳洲坚果放在托盘上，由进料口进入加热腔体后均匀输送到出料口，然后将托盘再次放入到进料口后进行加热，重复这一过程经过6次循环干燥湿基含水率降到1.5%以下。干燥过程中根据设计的时间点，随机取出若干颗澳洲坚果当其冷却后测量水分含量，绘制干燥曲线，建立数学模型，计算水分扩散系数与活化能。

2.2.1 干燥曲线的测定

(1) 干基含水率：

(2)

式中：

M——干基含水率，%；

mw——样品水分质量，g；

md——绝干样品质量，g。

(2) 水分比：

(3)

式中：

MR——水分比；

Mt——t时刻的含水率，g/g；

Me——平衡含水率(在一定的干燥条件下，将澳洲坚果干燥至恒重时的含水率)，g/g；

M0——初始含水率，g/g。

综上所述,MRCP在胆道结石中的诊断准确性、特异度、敏感度均较CT高,尤其是对于直径<0.8cm胆道结石的诊断较CT检查有明显优势,可在临床推广。

(3) 干燥速率：

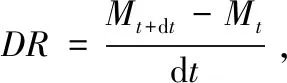
(4)

式中：

DR——干燥速率，g/(g·min)；

Mt+dt——t+dt时刻的含水率，g/g；

Mt——t时刻的含水率，g/g；

t——时间，min。

从进干燥开始为起始0点，通过设定传送带转速物料每1 h刚好通过整个隧道，每隔1 h测量澳洲坚果干基含水量，分别绘制澳洲坚果干燥曲线与干燥速率曲线。

2.2.2 干燥数学模型 物料干燥伴随着复杂的传热传质，为了描述这一过程，探明物料所含水分随干燥时间的变化机制，学者[16-19]通过大量的试验与理论分析，建立了多个经验与理论模型。试验选择了11个常用的薄层干燥模型(表1)进行澳洲坚果中红外干燥动力学研究并利用1Stopt软件进行数据拟合，R2越接近于1，RMSE和χ2越小，表明模型可靠性越高[20-21]。

2.2.3 有效扩散系数 表征水分传递的重要参数，表明物料的脱水能力，可运用Fick扩散第二定律来求解[22-25]，物料表层与外部环境之间的水分传递达到瞬态平衡时，不考虑干燥样品的体积变化及外部阻力，通过化简后得出有效扩散系数的表达式：

(5)

式中：

MR——水分比，%；

Deff——有效扩散系数，m2/s；

t——干燥时间，s；

L——物料厚度的1/2，m。

在式(5)中将t作为自变量，lnMR作为对应变量绘制函数曲线并进行一维线性拟合得到的直线斜率k如式(6) 所示。

(6)

2.2.4 干燥活化能 干燥活化能表征了物料干燥的难易程度。利用阿伦尼乌斯公式(Arrhenius equation)可以建立有效水分扩散系数、干燥温度与活化能之间的关系[26]，如式(7)所示。

(7)

式中：

Deff——有效扩散系数,m2/s；

D0——扩散基数，m2/s；

Ea——活化能，kJ/mol；

T——干燥温度，℃。

2.2.5 数据处理 试验数据使用Oringin 8.0绘图，利用1Stopt 15进行统计分析与数据拟合。

3 结果与分析

3.1 澳洲坚果中红外干燥特性分析

3.1.1 澳洲坚果中红外干燥曲线 由图2可知，澳洲坚果初始水分比为1(23.19%)，经过6 h水分降至0.05(1.36%)的安全水分。从图3可以看出，整个干燥过程主要呈现降速干燥，在初始阶段干燥速率较大，随后逐渐降低。可能是初始干燥阶段物料水分含量高，吸收的中红外能量高，同时利用冷却风机形成空气对流，实现澳洲坚果的热质同向传递，提升了干燥驱动力，形成较高的干燥速率。而随着干燥的进行，澳洲坚果水分含量与耦合能力均逐渐降低，同时澳洲坚果中亲水性固体表面与干燥剩余水分之间的结合力变大，进而造成蒸发焓逐步升高，导致水分去除能耗也相应增大[27]。因此，干燥速率将会持续降低直到干燥结束。

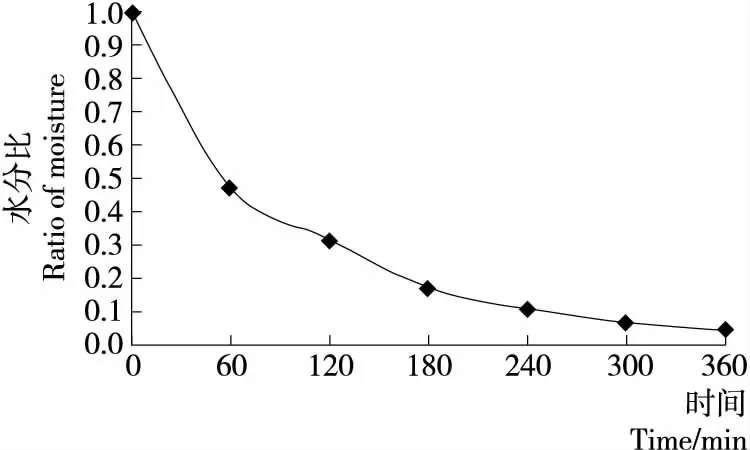
图2 澳洲坚果中红外干燥曲线Figure 2 Mid infrared drying curve of macadamia

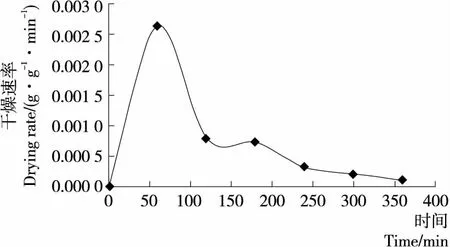
图3 澳洲坚果中红外干燥速率曲线Figure 3 Mid infrared drying rate curve of macadamia

3.1.2 澳洲坚果中红外干燥质传递与能耗 利用式(5)计算澳洲坚果干燥有效水分扩散系数，结果如图4所示，各阶段的干燥有效水分扩散系数在2.03×10-7～2.31×10-7m2/s，分布较均匀，符合农产品干燥区间。根据阿伦尼乌斯方程，结合式(7)可知，lnDeff与1 000/T+273.15呈线性关系，利用1Stopt软件进行拟合，计算出澳洲坚果的活化能为159.5 kJ/mol，与相关报道[27]的数值接近，相比苹果[28]、油茶籽[29]、燕麦马铃薯复合面条[30]活化能较大，因此较难干燥。

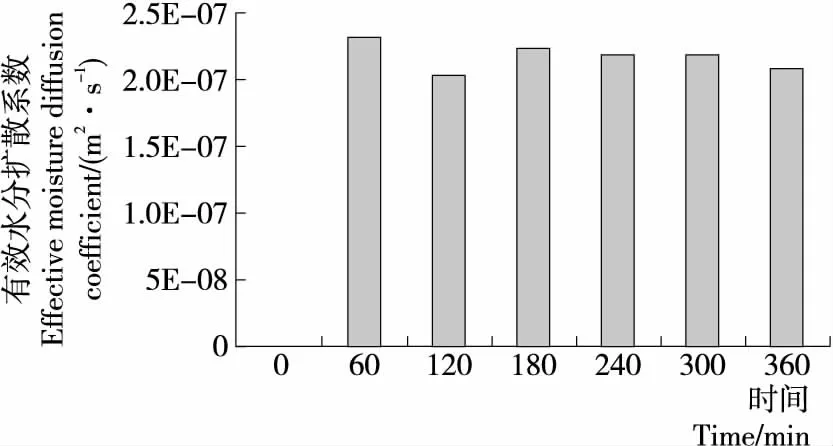
图4 不同时间点干燥有效水分扩散系数Figure 4 Effective moisture diffusivity at different time points

3.1.3 澳洲坚果中红外干燥裂纹分析 从外观上看澳洲坚果干燥过程中有微裂纹产生，主要是初始含水率较高，瞬态温度过高，导致局部干燥不均匀而形成的。目前红外干燥过程中难以避免细微裂纹的产生，即使采用热风低温干燥也可能产生，但细微裂纹对贮藏影响有限或许还有利于后续的开口及脱壳。经试验发现，提高控制精度、及时散热处理等措施可进一步降低裂纹产生、减小裂纹大小。

3.2 澳洲坚果中红外干燥动力学模型研究

由表1可看出，Midilli-Kucuk模型的R2值最大，RMSE与χ2平均值最小，因此Midilli-Kucuk可以有效地描述澳洲坚果中红外干燥过程，方程可以表示为：

MR=0.999 3exp(-0.030 1t0.7643)-5.414 5E-005t。

(8)

表1 各模型与统计结果分析Table 1 Name and statistical analysis of each model

3.3 澳洲坚果中红外干燥试验验证

针对Midilli-Kucuk模型利用同一批次澳洲坚果进行中红外干燥，测量不同时间点的水分进行验证，结果如图5 所示，拟合效果好，说明Midilli-Kucuk模型可以有效地预测澳洲坚果中红外干燥过程中的水分变化情况。

4 结论

(1) 研制了中红外干燥机，确定了辐射器种类、加热功率、辐射距离等主要参数，并制定了调质降温的控制方法，促进水分热质同向传递，提升干燥驱动力，干燥时间显著缩短，较好地解决了均匀干燥问题。

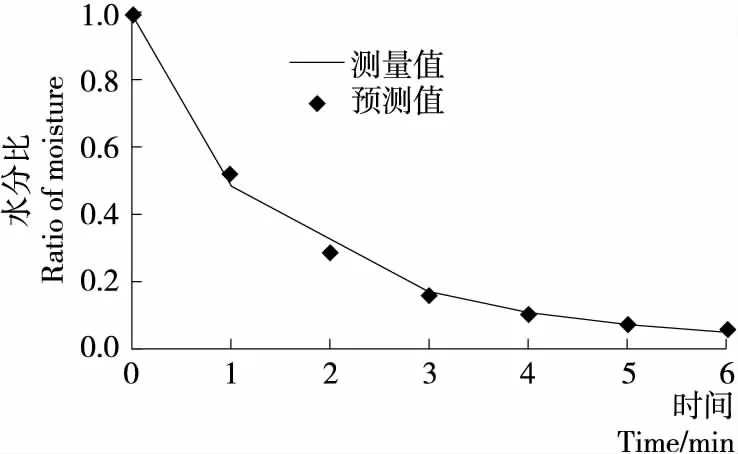
图5 Midilli-Kucuk模型下预测值与试验值对比

Figure 5 Comparison between predicted value and experimental value under Midilli-Kucuk model

(2) 澳洲坚果通过中红外干燥，经过6 h由23.19%的初始含水率降到1.36%的安全水分，整个过程主要为降速干燥，无明显恒速干燥阶段；Midilli-Kucuk方程可以较好地预测澳洲坚果中红外干燥过程水分的变化机制。

(3) 澳洲坚果中红外干燥各时段有效水分扩散系数位于2.03×10-7～2.31×10-7m2/s，分布较均匀，符合农产品干燥区间；澳洲坚果的活化能为159.5 kJ/mol，高于一般果蔬，进一步从理论上说明了其干燥困难的原因。

(4) 澳洲坚果干燥过程中有微裂纹产生，应继续优化设备的温度控制系统，进一步提升澳洲坚果干燥的均匀性，减少微裂纹产生或使其大小满足生产要求。