基于Smith预估补偿的啤酒发酵温度控制策略

高 锦 章家岩 冯旭刚

(安徽工业大学电气与信息工程学院，安徽 马鞍山 243032)

啤酒发酵是啤酒酿造过程中最为关键的环节，该生产环节控制效果的好坏对于最终所生产酿造出的啤酒口感和质量起着决定性作用。发酵环节是一个复杂的生物化学反应过程，其中发酵罐中的压力、温度以及发酵液中的酵母浓度等均会影响到最终产物的质量。由于发酵液温度的变化会影响发酵罐内部压力以及发酵液中的酵母浓度，所以对于发酵温度的调节控制显得更加重要[1-4]。

常规的PID控制因其控制结构简单、良好的稳态性能等特点，而被许多啤酒生产厂商用于啤酒发酵过程中的温度控制。但该控制方法参数整定时间长，并且无法针对不同的温度控制条件修改控制参数，因此会导致控制系统的动态控制效果不佳[5-6]。目前国内外学者针对啤酒发酵温度控制问题开展了先进的控制策略的研究[7-8]，杜金钊等[7]采用模糊控制器控制啤酒发酵的温度，获得了良好的动态特性，但稳定性不理想；孙家琪等[8]提出了预测控制策略并进行了仿真，结果表明该方法具有良好的抗干扰性，但并未考虑模型失配的情况，在实际的应用中会有一定的偏差。

试验提出一种基于Smith预估补偿的非线性PID控制策略，以解决常规PID存在动态响应慢、超调量大等问题，提高系统的控制性能，确保啤酒发酵温度控制的准确性和快速性达到平衡，保证啤酒生产质量。

1 啤酒发酵温度分析及建模

1.1 啤酒发酵温度控制

啤酒发酵由于涉及到大量的生物化学反应，因而成为啤酒生产过程中最耗时的环节。简而言之，啤酒发酵就是糖化麦汁通过酵母菌的发酵作用，最终分解成C2H5OH、CO2、H2O的过程。在此期间，发酵罐内会产生诸如双乙酰、高级醇等产物。虽然此类产物的量极小，但其对啤酒最终的口感与质量却影响很大[9]。在正常情况下，较低的发酵温度可以降低酵母活性，影响发酵速率，并最终实现较小的发酵中间产物量；较高的发酵温度可以提高酵母活性，加快发酵速率，并最终提高生产效率和经济效益。所以实现对啤酒发酵过程中温度的精确控制是确保啤酒最终质量的重要举措。

啤酒的发酵是在体积较大的封闭发酵罐中进行的，罐内发酵原料的温度分布存在一定的梯度。因此，通常采取3段式温控策略，即分别设置上部、中部及下部3段温度冷却带，分别设置3个阀门，每层的温度检测采取3个温度检测器件均匀分布同时检测，最后取其平均值作为最终该层的温度检测值。该温度检测值作为最终所要实现的控制目标，同时可作为一个被控量用来指导调节阀门开度，即控制每层冷媒介质的流量值。

由于啤酒发酵罐中存在热对流现象，并且上部冷媒介质流量的大小也会影响中下部的发酵液温度。因此啤酒发酵温度控制系统是一个输入和输出之间存在耦合的系统。并且随着时间的变化，啤酒发酵所要求的温度会有所变化，因此该系统还是一个时变系统。通过对大量现场采集的数据进行分析，可确定本系统的多输入多输出之间虽然存在耦合关系，但耦合作用不是很强，基本上每层的温度控制回路就可以进行单独控制。由于发酵罐上部的液体大多是气液混合物，而发酵罐下部通常为酵母堆积的液体，因而上部测温点和下部测温点所检测到的温度值通常不作为控制量。因此将中部测温点检测到的温度值作为主要控制量。

啤酒发酵的工作原理：控制系统通过温度传感器实时测量发酵罐中的温度变化，并将其传送到PC，进而传送给PLC控制器，控制器向电磁阀传输信号以调节阀门的开度，从而改变冷媒介质流量。冷媒介质通过发酵罐壁与发酵罐内发酵液进行热交换，最终使得发酵液的温度控制在理想的温度范围内。

从图1可以看出，啤酒发酵温度工艺主要可以分为1个自然升温阶段、3个保温阶段以及2个降温阶段三部分。其中前期的自然升温阶段由于是生化反应放热速率慢，因而调控简单，采用常规PID控制即可满足控制要求。3个保温阶段主要指的是前酵阶段、还原阶段和低温贮酒阶段，由于该阶段的主要控制目标是保持温度不变，不出现较大的超调或者抖动，因而对其进行控制也不难。主要的控制难点在两个降温阶段，因为降温阶段要求等速降温，而自然升温阶段所产生的热量较少，另外，使用冷媒冷却降温会有时间滞后，所以采用常规PID对啤酒发酵温度进行调节控制会产生较大超调量，较慢的响应调节，进而导致温度的误差偏大，影响最终的啤酒质量[10-11]。基于此，选择更加先进的控制算法来实现对两个降温阶段的温度控制尤为重要。

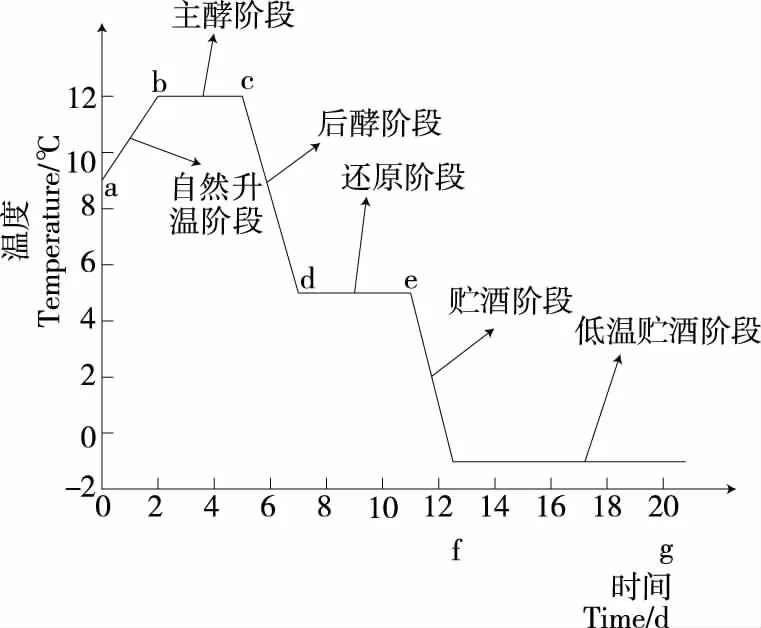
图1 啤酒发酵过程中的温度工艺曲线Figure 1 Temperature curve during beer fermetation

根据啤酒发酵过程中的温度工艺要求，设计了一种基于Smith预估补偿的非线性PID控制器来调节啤酒发酵温度，如图2所示。

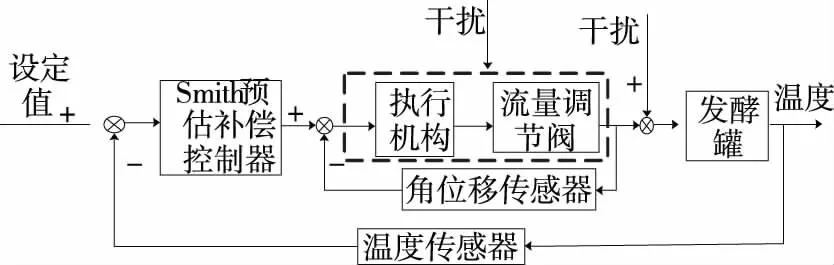
图2 啤酒发酵温度控制原理

Figure 2 The temperature control principle of beer fermentation

考虑到啤酒生产过程中的复杂环境，作用在流量调节阀的各种干扰将导致其开度不准确。因此，执行器与调节器之间采用闭环控制，最终实现流量调节阀的准确定位。由于啤酒发酵过程中，微生物在发酵罐中持续不断的生化反应，发酵罐内的温度不断变化，因此为了保证发酵温度按照理想的发酵温度曲线进行变化，需要对发酵罐中温度进行监测并反馈给温度设定值，最终实现自动控制。

1.2 啤酒发酵温度模型

由于啤酒发酵的反应机理复杂，采用机理建模方法很难获得精确的温度模型，但可以据此对发酵温度模型所具有的一些动态特性进行分析[12-14]。因此，可以根据发酵过程中生物化学反应的热平衡原则来对啤酒发酵温度模型进行近似描述[15]。由于发酵罐的体积大，因此进行模型构建时，需做出如下假设：

① 考虑某固定时间段的一段发酵过程；

② 忽略微生物生长产生的热；

③ 忽略热传递时的热损失；

④ 忽略冷媒介质、发酵罐壁和发酵液三者之间的温度变化梯度。

根据热平衡原理和以上假设，可以建立以下方程：

(1) 发酵液和发酵罐壁两者之间的热平衡方程[16]：

(1)

式中：

C——比热容，J/(kg·℃)；

M——发酵液的总质量，kg；

θ——发酵液的实时检测温度，℃；

θ0——发酵罐壁的平均温度值，℃；

E——发酵反应产生的热量，J/s；

k——发酵罐壁和发酵液之间的传热系数，J/(m2·s·℃)；

S——发酵液和发酵罐内壁之间的接触面积，m2。

(2) 冷媒介质和发酵罐壁两者之间的热平衡方程[17-19]：

(2)

式中：

C1——发酵罐壁的比热容，J/(kg·℃)；

M1——发酵罐壁的总质量，kg；

k1——发酵罐壁和冷媒介质之间的传热系数，J/(m2·s·℃)；

S1——发酵罐壁和冷媒介质之间的接触面积，m2；

θ1——冷媒介质的平均温度值，℃。

(3) 冷媒介质的热平衡方程：

k1S1(θ0-θ1)=ρQC2(θ3-θ2)，

(3)

式中：

ρ——冷媒介质的密度，kg/m3；

Q——冷媒介质的流量，m3/s；

C2——冷媒介质的比热容，J/(kg·℃)；

θ2——冷媒介质的入口温度值，℃；

θ3——冷媒介质的出口温度值，℃。

根据式(1)～(3)，可推导得出：

s(T1s+1)θ(s)=-aQ(s)+b(T2s+1)E(s)，

(4)

整理后得：

(5)

式中：

E(s)——啤酒发酵时产生的热量，J/s；

Q(s)——冷媒介质的流量，m3/s；

a、b——常值；

T1、T2——时间常数。

在啤酒发酵过程中，发酵液温度是影响酵母活性的重要因素，而酵母活性则是反应过程活跃程度的衡量标准，酵母活性高，反应速率也就高，反之反应速率低。因此，根据阿伦尼乌斯(Arrhenius)公式，发酵反应速率和发酵温度之间的关系可表示成[20]：

(6)

式中：

μ——发酵反应速率，mol/(L·min)；

α、β——常数；

θ——发酵液的实时检测温度，℃。

由于发酵罐中没有搅拌装置，所以发酵罐中热量的交换传递主要通过发酵罐内的发酵液相互对流的方式进行。基于此，在对发酵温度对象的特性进行分析研究时，θ既是时间上的函数，也是空间上的函数。综上所述，通常将发酵液的实时检测温度θ和冷媒介质的流量Q之间的关系近似描述为二阶时滞特性，其表达式如下：

(7)

式中：

T3、T4——时间常数；

τ——滞后时间，s；

K——增益系数。

2 啤酒发酵温控系统算法

由于啤酒发酵过程中不同时间段对应的工艺要求以及温度控制要求有所区别，因此常规PID控制无法有效满足。在这种情况下，试验依据自适应控制和智能控制的基本思想并借助于计算机的优势而采用非线性PID控制算法[21]。另外，由于啤酒发酵温度控制系统的大延迟和非线性，使用Smith预估器对其进行补偿。图3为采用Smith预估补偿的非线性PID的控制系统框图。

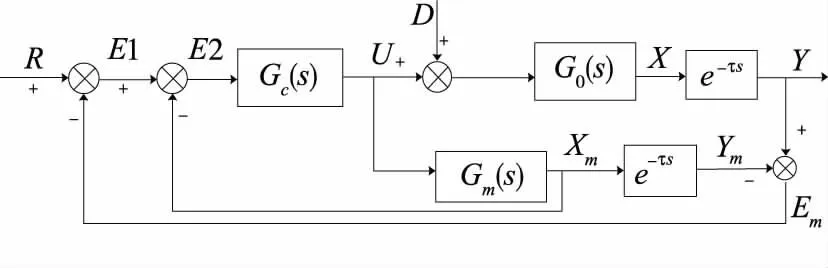
Gc(s). 控制器的传递函数G0(s). 控制系统实际的模型Gm(s). 控制系统的参考模型R. 系统的给定量D. 系统的扰动量Y. 系统的实际输出Ym. 参考输出τ. 该系统的纯滞后时间常量

图3 Smith预估补偿的非线性PID控制系统

Figure 3 Smith predictive compensation nonlinear PID control system

非线性PID控制器Gc(s)的设计基于高斯函数。构造如下非线性函数kp、ki、kd：

kp[e(t)]=ap+bp{1-exp[-(e〔t〕/cp)2]}，

(8)

式中，ap、bp、cp为正常数。当误差e(t)→±时，kp取最大值ap+bp；当e(t)=0时，kp取最小值ap；bp为kp的变化区间；cp的大小是kp变化的速率。

(9)

式中，ap、bp、cp为正实数，ad为kd的最小值，ad+bd为kd的最大值，当e(t)=0时，kd[e(t)]=ad+bd{1-exp[-(dd/cd)2]}，kd的变化速率可通过调整cd大小来进行调节。

ki[e(t)]=aiexp[-(e(t)/ci)2]，

(10)

式中，ki的取值范围为(0,ai)，e(t)=0时，ki取最大值。ci的取值决定了ki的变化快慢程度。

比例增益参数kp函数的变化曲线如图4(a)所示。从图4(a)中可以看出，当e(t)>0时，为保证系统有更快的响应速度和更小的超调量，kp随着e(t)的增大而增大。当e(t)<0时，随着|e(t)|的增大，为了保证系统具有好的快速性和小的超调量，kp也随之增大；当|e(t)|减小时，为使系统尽快回到稳定点，kp也应减小。

微分增益参数kd函数的变化曲线如图4(b)所示。从图4(b)中可以看出，当系统的超调增加时，kd迅速增大，反向控制作用随之增强，因此系统超调量被有效抑制。

积分增益参数ki函数的变化曲线如图4(c)所示。从图4(c)中可以看出，当e(t)较大时，为了避免系统的响应产生振荡和减小系统的超调量，ki不应该选取得过大；当e(t)较小时，为了消除系统的稳态误差，ki要增大。

非线性PID调节器的控制输出为

(11)

非线性PID调节器中的增益参数会随控制误差而变化，因而其抗干扰能力强于常规线性PID控制器。

3 试验仿真及分析

在对一200 L的小型啤酒发酵罐的发酵温度控制系统进行建模之后，确定数学模型为

(12)

图4 kp、kd、ki的变化曲线Figure 4 kp、kd、ki change curve

式中：

K——放大系数，K=1；

T——时间常数，T=8；

τ——滞后时间常数，τ=3。

运行时间为2 000 s。当运行时间为1 000 s时，向系统添加一个幅值为0.05的阶跃信号作为干扰信号。根据仿真结果，基于Smith预估补偿的非线性PID控制具有更好的抗干扰性。表1为两种控制器的动态性能指标对比情况。

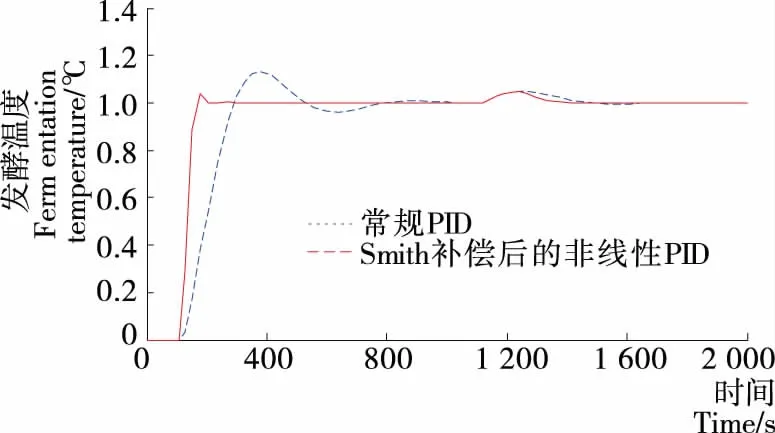
图5 啤酒发酵温度控制仿真曲线

Figure 5 Simulation curve of beer fermentation temperature control

表1 控制器的动态性能指标Table 1 Controller dynamic performance indicators

从图5和表1可以看出，Smith预估补偿的非线性PID控制优于常规PID控制，具有更好的动态性能和抗干扰性，更短的响应时间，更小的超调量。

在实际的啤酒发酵温度控制系统中，由于阀门等设备的老化、校测中存在的误差等原因，整个系统具有不确定性，所以采用参数摄动对其进行描述。被控对象随机摄动可写成如下形式：

(13)

式中，选取p的摄动区间为[-0.1，+0.1]，即被控对象的3种摄动情况分别为p=+0.1，p=0，p=-0.1。阶跃信号用于仿真分析，K的摄动仿真曲线如图6所示。

由图6可知，当K在摄动区间[-0.1，+0.1]随机波动时：如果增益K增大，则该控制器跟随设定值的响应速度变快，调节时间变短；如果增益K减小，则该控制器跟随设定值的响应速度变慢，调节时间变长。但最终所有的均可趋于稳态。因此，当参数K摄动时，试验所设计的控制系统可以保持比较好的鲁棒性和动态控制品质。

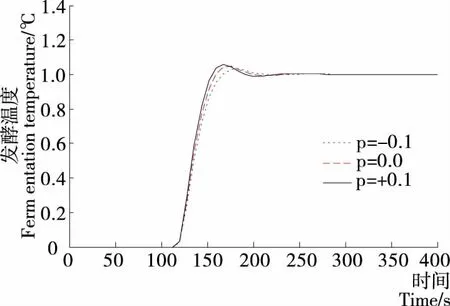
图6 K的摄动仿真曲线Figure 6 K’s perturebation simulation curve

4 应用案例

对于200 L的小型啤酒发酵罐的啤酒发酵温度控制系统，使用现有的西门子S7-300PLC作为控制器，用力控组态软件进行上位机监控程序的开发，控制器调节周期设置为7～9 s。用SCL语言进行编程，将编写的FB1作为非线性PID控制器，而编写的FC1用于计算kp、ki、kd的值。上位机可显示啤酒发酵温度的变化趋势。图7、8分别为应用常规PID和Smith预估补偿的非线性PID时的啤酒发酵温度波动曲线图。图7中3个保温阶段的温度控制范围分别为±1.0，±0.5，±0.7 ℃。图8中3个保温阶段的温度控制范围分别为±0.30，±0.25，±0.30 ℃。后者具有比前者更高的控制精度，而后者对于外部的扰动具有很强的抗干扰能力。

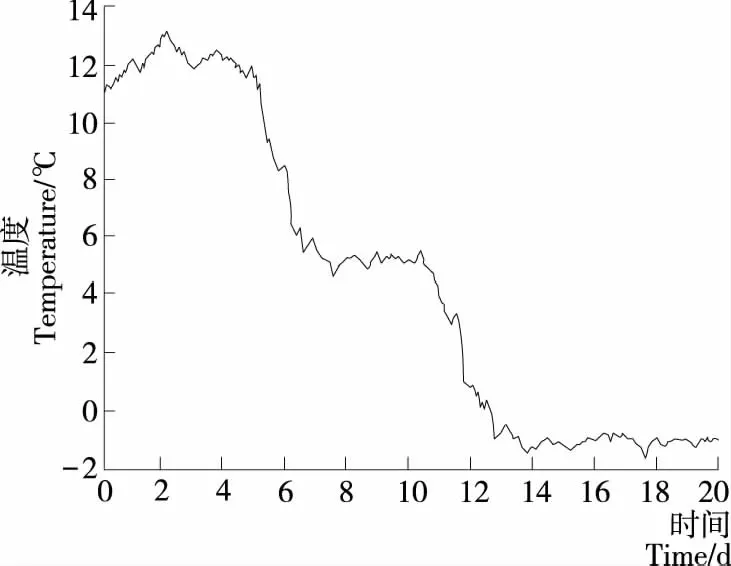
图7 常规PID应用曲线Figure 7 Application curve of conventional PID

图8 Smith补偿的非线性PID应用曲线Figure 8 Smith compensation nonlinear PID application curve

5 结论

研究介绍了啤酒发酵温度控制的工艺流程，针对啤酒发酵温度所具有的大时滞性和分阶段性等特点，提出基于Smith预估补偿的非线性PID控制策略。与已有的研究差异在于有效地提高了温度控制的快速性和稳定性，并具有较强的抗干扰能力，此外，研究运算简单，适合工厂的应用，可以满足啤酒发酵温度的控制要求。

尽管研究的控制策略较简单且实用，但啤酒发酵温度是个建模难的过程，研究也只针对几个重要的特点来设计控制器，寻找更精确的对象模型是下一步研究的重点，而且建模过程中的影响因素较多，需要较多的实际经验，都有待于进一步的研究。