科学思维素养方面“模型建构”5级水平的表现性任务设计

唐黎明

(宝山区教育学院，上海 201900)

教育部制定的《普通高中物理课程标准(2017年版)》(简称《标准》)简要介绍了高中物理课程核心素养的4个方面,它们分别是物理观念、科学思维、科学探究和科学态度与责任．随着课改的推进,近几年有关核心素养的研究在我国基础教育界正如火如荼地进行．

1 问题的提出

《标准》认为科学思维主要包括模型建构、科学推理、科学论证、质疑创新等要素．《标准》中《附录Ⅰ 物理学科核心素养的水平划分》关于科学思维的5级水平要求如表1所示．

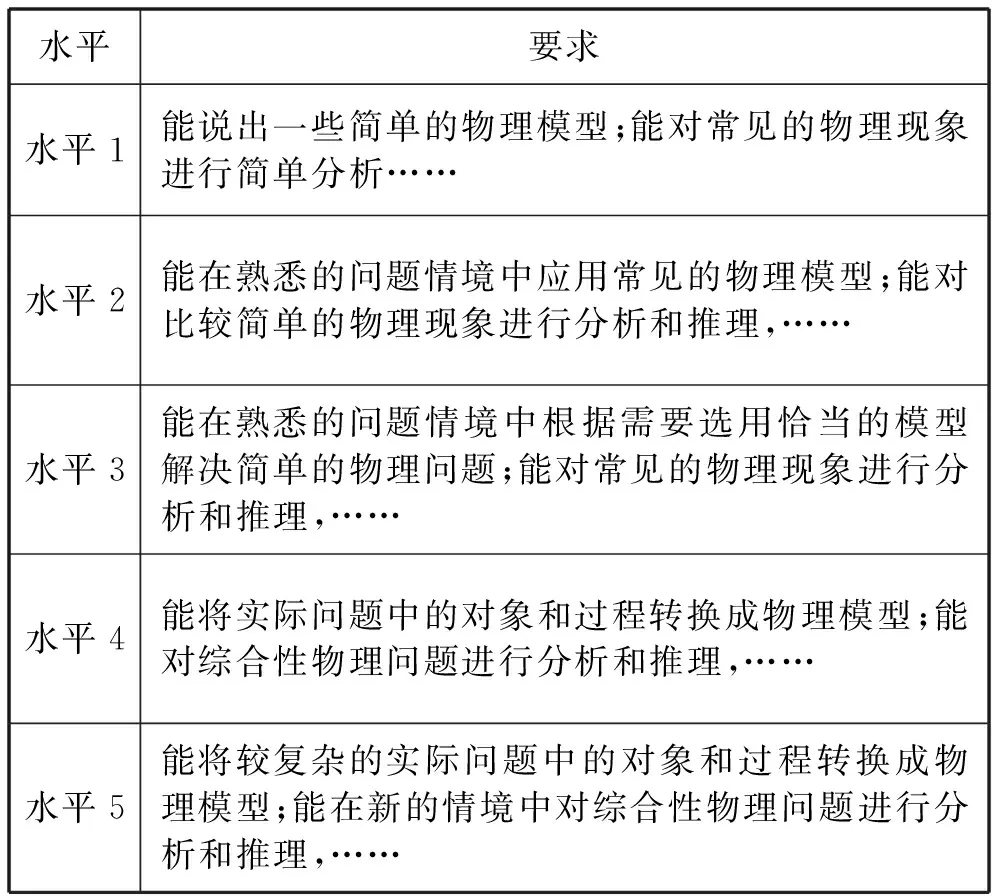
表1 科学思维素养的5级水平[1]

将表1中水平1至水平5要求的内容分别与模型建构、科学推理、科学论证、质疑创新对应起来,就会分别得到模型建构、科学推理、科学论证和质疑创新的5级水平要求．其中“模型建构”的5级水平要求如表2所示．

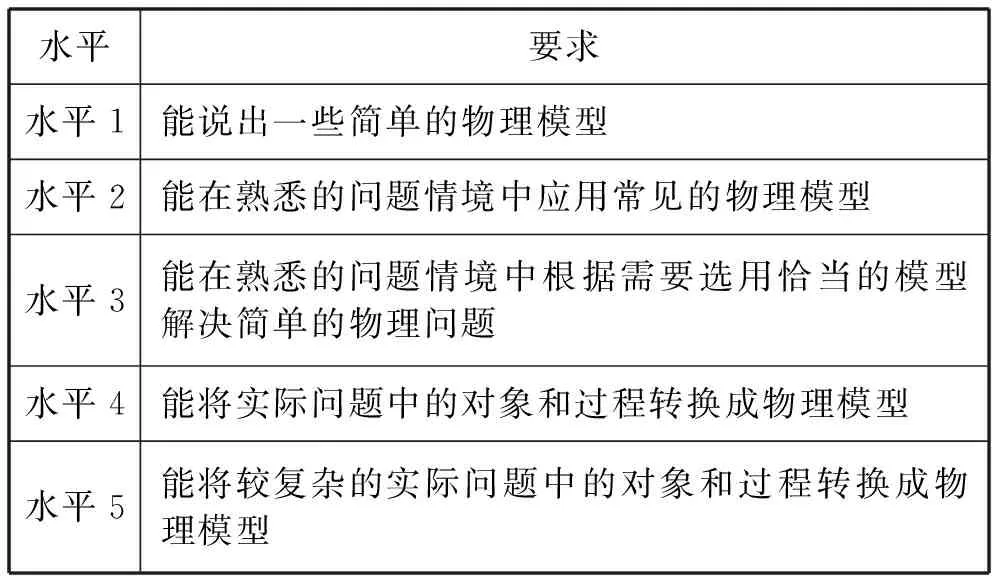
表2 模型建构的5级水平

但《标准》并未给出表2中“模型建构”5级水平的表现性任务的样例.这里指的表现性任务是指分别符合表2中5级水平要求的任务．没有这样的样例无论关于“模型建构”的教学还是对于其测评,都会有一定的困难,教师们会琢磨不定、难以把握要求.这不利于《标准》在一线课堂的实施,也不利于核心素养的目标落实．为了在一定程度上缓解这样的窘境,笔者将尝试依据表2中关于“模型建构”5级水平的要求分别设计相应的表现性任务的样例,并分别阐述它们的特征．

2 模型建构的水平1

表2中水平1的要求是这样的:能说出一些简单的物理模型．

在《学习、教学和评估的分类学》一书中,将认知过程中的理解维度分为解释、举例、分类、概要、推论、比较和说明7个亚类,其中关于举例的描述有“举例出现在学生提供一般概念或原理的例子的时候．…例子或事例是学生未曾在教学中见到的．”[2]那么 “水平1”是否可以认为是理解维度中的举例呢?“水平1”从语义上来说就是能例举几个物理模型,但不表明不可以举教学中已出现过的例子,所以水平1不能被认为是“举例”,也就不能被认为是认知过程中的理解维度,在5个等级中水平1又是最低的,所以认为水平1是一个知道级水平,是合理的,知道级水平包括再认和回忆．

“再认”涉及从长时记忆中提取相关知识以便将它与呈现的信息进行比较．[2]

例1.下列选项中属于物理模型的是

(A) 带电体. (B) 电子.

(C) 点电荷. (D) 元电荷.

由于学生已经学过“点电荷是一个物理模型”,在他们的长时记忆中应该有这样的记忆,只要将这个记忆与样例呈现的信息进行比较,就能得出答案(C),所以本例的认知要求是再认．

“回忆”涉及在给予提示的条件下,从长时记忆中提取适当知识．[2]

例2.请举出物理模型的2个例子．

本例要求学生从长时记忆中提取已学过的物理模型的例子,与例1相比没现成的答案可供辨认,需要将答案回忆出来,所以例2的认知要求是回忆．

3 模型建构的水平2

表2中水平2的要求是这样的:能在熟悉的问题情境中应用常见的物理模型．

“水平2”中“熟悉的问题情境”和“常见的物理模型”应该是学生在平时的教学或生活中习以为常的,至少是不陌生的、容易想到的．应用常见的物理模型,实际上是应用作出常见的物理模型是否适用的判断的规则,也就是“应用行为”是受这个规则支配的．

比如“应用质点”,实际上是应用作出质点是否适用的判断的规则,判断质点是否适用的规则是:如果研究的问题与物体的大小和形状无关,或物体的大小和形状对于研究的问题来说可以忽略,那么物体可以被看作质点．规则的条件部分就是《标准》中讲的“质点的条件”,[1]不妨把这个规则叫做“质点的条件”,当面对问题需要判断研究对象是否可以被看作质点时,学生应该受到规则“质点的条件”的支配,所以为了表达类似 “应用质点”的教学要求时,还不如讲类似“应用质点的条件”来得明确．

从R.M.加涅的学习结果分类来看像这种受规则支配的智慧技能称为规则,因此,“水平2”应该对应于R.M.加涅所说的学习结果中的规则,规则是通过其运用于一个或多个具体例证而得以展示的．[3]

例3.研究下列与运动物体有关的问题时可将物体视为质点的

(A) 研究航天飞机绕地球作圆周运动的半径.

(B) 研究转动车轮边缘的速度.

(C) 研究运动员跳高时的过杆动作.

(D) 研究列车全部通过铁路桥所需的时间.

本例要求运用“质点的条件”来作出选择,各个选项中的问题情境是熟悉的,质点也是常见的物理模型,所以是一个符合水平2的例子．由于航天飞机的大小比其圆周运动的半径要小得多,所以在(A)选项的问题情境中可将航天飞机视为质点,若选择了(A),则表明出现了受“质点的条件”支配的行为．如果能正确完成类似样例2的多个任务(例如运用“理想气体的条件”、运用“简谐运动的条件”等规则),则可以表明关于物理模型的学习达到了水平2．

4 模型建构的水平3

表2中水平3的要求是这样的:能在熟悉的问题情境中根据需要选用恰当的模型解决简单的物理问题．

比较“水平3”和“水平2”,相同的是“熟悉的问题情境”,不同的是“水平3”中多了“解决简单的物理问题”,“水平3”中“根据需要选用恰当的模型”是以“解决简单的物理问题”为目的的．所以水平3比水平2具有较高的等级要求表现在“解决简单的物理问题”上,对于水平3,不但要像水平2那样应用物理模型(实际上运用物理模型的条件),而且要能“解决简单的物理问题”．因此,水平3是一种“运用物理模型的条件”技能和“解决简单的物理问题”技能的综合技能．一个表现水平3的例题如下.

例4.一辆汽车正在以15 m/s的速度行驶,司机发现前方红灯亮起,立即刹车,刹车过程中汽车的加速度大小是6 m/s2．若司机刹车时汽车距离前方斑马线约20 m,请问司机是否有可能闯红灯?

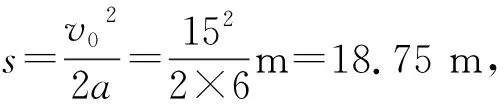
例4中的刹车情境是一个“熟悉的问题情境”,解答中只用到了一个物理公式,那么当有计算时“用一个物理公式” 就作为“解决简单的物理问题”的一种标志吧．

图1

图2

例5.如图1所示,有一根足够的竖直玻璃管,下端封闭,内有一段h=4 cm的水银柱,水银柱的下面封闭着长L1=60 cm的空气柱,大气压强为76 cmHg．如图2所示,若向管内缓缓注入20 cm长水银,则空气柱L2有多长?

解析：解决本样例首先运用等温变化的条件,由于样例中有“缓缓注入”,应将玻璃管中气体的状态变化看作等温变化这一物理模型,其次运用玻意耳定律．

先计算气体第1状态时的压强,

p1=p0+ph=76+4=80(cmHg),

同理,有p2=100 cmHg.

由玻意耳定律,得p1SL1=p2SL2,

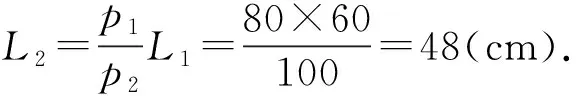
在计算中也用到了一个物理公式(玻意耳定律),尽管有压强计算,但在这一问题中重要的是玻意耳定律的运用,在这里还是体现了“用一个物理公式”的原则．给出例5是想说明当“用一个物理公式”作为“解决简单的物理问题”的一种标志时,不是没有其他辅助性的计算或判断参与问题解决.这些辅助性技能的运用为水平3在一定程度上的“弹性”变化成为可能.事实上我们做不到举出的二个样例精准地在同一水平上,可以做到的是能够将一些样例合理地控制在一个水平区间内．

5 模型建构的水平4

表2中水平4的要求是这样的:能将实际问题中的对象和过程转换成物理模型．

从要求的内容上来看,水平4和水平3存在明显的不同,“水平4”中明确提出“实际问题”,而不是“水平3”中的“熟悉的问题情境”,当然“实际问题”可能也是熟悉的,但也可以是不熟悉的、新颖的,如果是后者,那么难度就增加了．“水平4”中又明确提出将“对象和过程转换成物理模型”,存在二种转换;而对于水平2或水平3来说,应该只有一次“应用”或“选用”．“水平4”中的“转换”是在思考解决“实际问题”(不同于“简单的物理问题”)的目标下引导的,将“对象和过程”转换为物理模型是解决这类问题的前提．还有“水平4”不像“水平3”那样提出类似“解决简单的物理问题” 的要求,即“水平4”没有提出“解决实际问题”的要求．

例6.跳绳是一种健身运动,某运动员1 min跳180次,假定在每次跳跃中,脚与地面的接触时间占跳跃一次所需时间的2/5,为了能够算出该运动员跳起的最大高度，

(A) 将跳绳中的运动员视为质点.

(B) 将运动中的绳子视为质点.

(C) 将在空中的运动员看作只受重力的作用.

(D) 将跳绳看作简谐运动.

本例涉及“计算跳绳时的最大高度”这一实际问题,根据水平4,例题的作答反应不要求计算这一高度,例题的4个选项分别叙述了为了解决这一实际问题将“对象和过程转换成物理模型”的有关情况．将运动员视为质点并不难,所以(A)选项容易选对.稍难的是当有了“计算跳绳时的最大高度”正确方案(主要是将运动员在空中的运动看作竖直上抛运动)时,才有可能选对(C)．选项(C)之所以没有设计成“将运动员在空中的运动看作竖直上抛运动”是为了避免直白地向学生暗示解决这一问题的思路,以本例题符合“水平4”．值得提醒的是设计选择题时,要考虑选项间的“迷惑”性,[4]在本样例中企图用选项(B)来“迷惑”选项(A), 用选项(D)来“迷惑”选项(C),以减少“猜对”答案的可能性．

6 模型建构的水平5

图3

表2中水平5的要求是这样的:能将较复杂的实际问题中的对象和过程转换成物理模型．

“水平5”和“水平4”明显是类似的,“水平5”比“水平4”只多了“较复杂的”,用它来修饰“实际问题”,以突出水平5比水平4要求高．

例7.如图3所示,是建筑工地上常用的一种“深坑打夯机”．工作时电动机带动两个紧压夯杆的滚轮匀速转动,可将夯杆从深h=4.8 m的坑中以2 m/s2的加速度由静止竖直向上提起来．当两个滚轮与夯杆分开时,夯杆被释放,最后夯杆在自身重力作用下落回深坑,夯实坑底．之后两个滚轮再次压紧,夯杆再次被提上来,如此周而复始工作．已知两个滚轮边缘的线速度恒为5 m/s,假定在打夯过程中坑的深度变化不大,且夯杆底端升到坑口时,速度恰好为0(不计夯杆在坑底停留的时间)．为了计算打夯的周期应将夯杆看作什么物理模型?并分析夯杆在一个周期内做的是怎样的运动?(g=10 m/s2)

本样例涉及“计算打夯周期”这一实际问题,根据“水平5”,样例的作答也不要求“计算打夯周期”,“计算打夯周期”是“对象和过程”转换的意图,样例的作答反应是“对象和过程”的物理模型的建立．本样例的解答如下.

由于夯杆上各点的运动情况都相同,要计算的是打夯的周期,所以只要观察夯杆底端的运动就可以了,即以夯杆底端的运动来代替整个夯杆的运动,将夯杆看作质点．

解析：假设夯杆在匀加速上升过程中速度尚未达到滚轮边缘的线速度5 m/s时,滚轮与夯杆分开,然后夯杆作竖直上抛运动(通常夯杆重力要比其受到的空气阻力大得多,忽略空气阻力),直至夯杆底端升到坑口时速度为0．

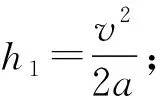
由于v<5 m/s,所以“假设”成立．

若从夯杆底端离开坑底算起,到夯杆底端首次回到坑底为一个周期,则夯杆先作匀加速直线运动,再作上升阶段的竖直上抛运动,最后做自由落体运动．

通过上述解答,不难发现样例5的复杂性一方面表现为运动过程的分阶段性,另一方面表现为,对于可能的运动过程并不是可以直接判断的,而是需要证明的．所以样例5应该符合“水平5”的要求．

7 小结

通过上述分别偿试例举模型建构的5级水平的样例,觉得有必要澄清5级水平的具体意涵,特在表2右侧加了一栏“附加说明”,内容见表3．

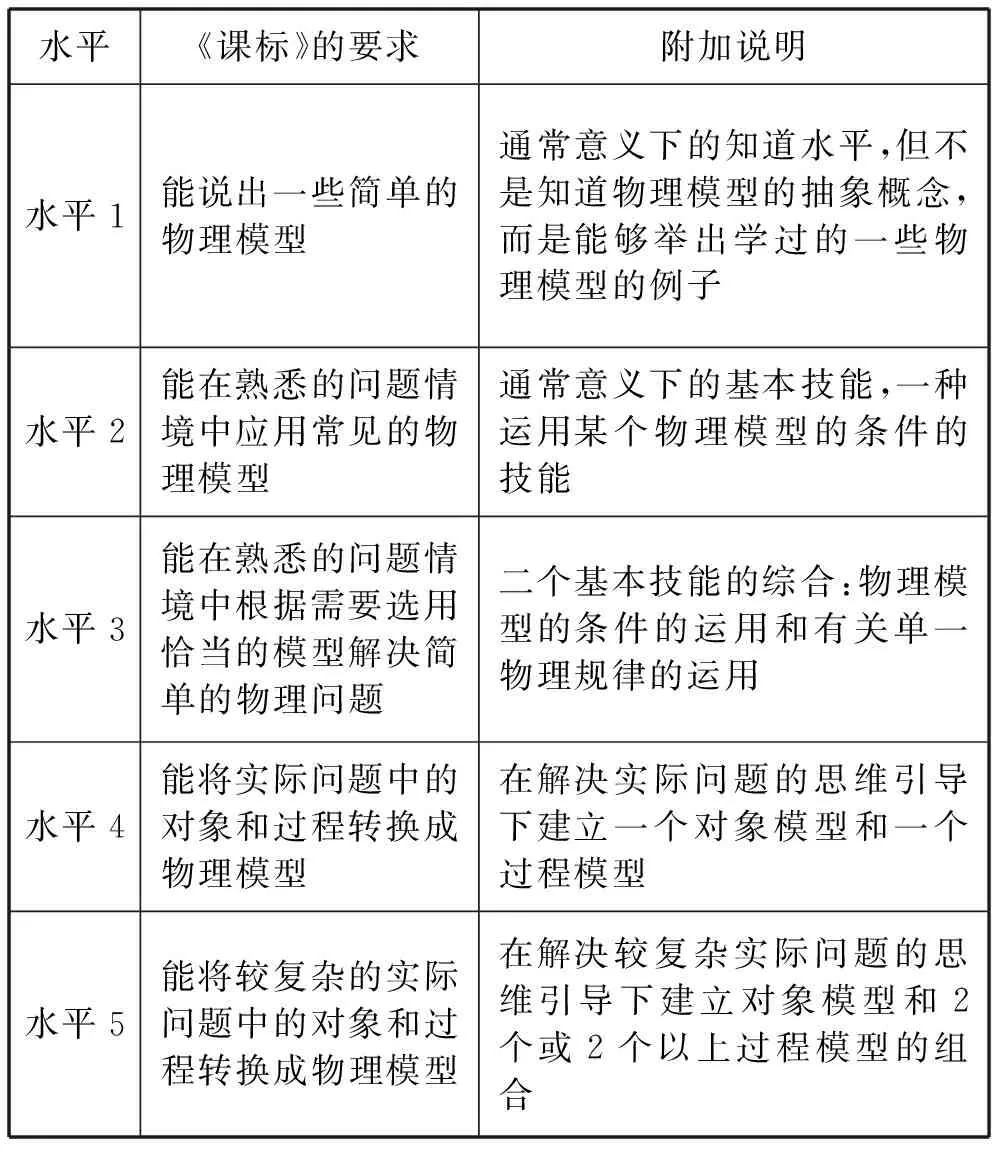
表3 模型建构的5级水平

另外,在分别设计模型建构的5级水平的表现性任务时,还可以采用下面“3个策略”．

(1) 模型建构的5级水平不可能是间断的,每级水平应该代表了一个水平区间．

(2) 关于体现模型建构各级水平的表现性任务,问题情境的复杂度[5]是逐渐增加的,所以物理模型也就“藏”得更深．

(3) 在设计体现模型建构3级以上水平的物理问题,表现性任务的完成不可能回避除了物理模型的条件性知识以外的其他物理知识或技能．这说明中等以上水平的模型建构能力是和其他物理知识的运用连结在一起的．

总之,“附加说明”和“3个策略”是本文通过尝试模型建构的样例设计而得出的结论.这些结论将为有兴趣开发足够的、训练或评估科学思维素养方面模型建构的表现性任务,提供策略性指导.

除模型建构外,科学思维素养方面还有科学推理、科学论证、质疑创新3个要素,希望有志之士能依次开展有关5级水平的表现性任务的样例研究,以便对科学思维5级水平有一个全面、合理而又明确的认识,本文若能起抛砖引玉的作用,笔者将深感欣慰．