应用STELLA软件研究非匀变速直线运动

刘文庆

(南京师范大学附属中学，江苏 南京 210003)

系统思考能够帮助我们理解并解决现实世界中复杂问题,用于支持系统思考的计算机模型有其特有的名称——系统动力学．系统动力学是一项计算机建模技术,能够对真实系统进行仿真,得出其时间特性．[1]STELLA软件在Windows操作系统下工作,是系统动力学用于建模的一种工具性软件．

运用系统动力学方法,思考做非匀变速直线运动物体的相关物理量之间逻辑关系,应用STELLA软件,构建系统循环图,即栈流图．从建模角度出发,栈流图有4个基本构造块,即栈、流、转换器、连接器．从系统思考的角度出发,栈流图由3个基本构造块组成,即栈、流和信息反馈．[2]STELLA软件具有强大的计算和作图功能,非常方便作出相应物理量随时间变化的图像和图表,可以定量研究变化的过程细节．本文笔者展示3个例子,应用STELLA软件,分别解决力学、电学、磁学中的非匀变速直线运动问题．

1 合外力随速度变化的非匀变速直线运动

情景1.质量是2 t的汽车,在平直的公路上行驶,如果汽车初速度是5 m/s,保持额定功率为80 kW,且运动过程中阻力不变,阻力是重力的0.2倍．问:汽车运动的加速度、速度如何变化?

f=0.2mg=0.2×2×103×10 N=4×103N.

由牛顿第二定律

开始,v0=5 m/s,牵引力为

合外力F合=F-f=1.2×104N,

最终,汽车以20 m/s收尾速度做匀速直线运动．

这个问题并不复杂,笔者以此为例,简要介绍应用STELLA软件解决问题的流程．

第1步,在Map菜单下,建立汽车恒功率加速过程物理量的逻辑关系的系统循环图如图1,速度是栈(Stock),加速度是流(Flow),质量、合外力、牵引力、功率、阻力、阻力系数都是转换器(Conventer),带箭头的连接两个物理量的线是连接器(Action connector)．图中诸多物理量构成一个相互作用的系统,注意到速度对牵引力的影响,逻辑上是负反馈．

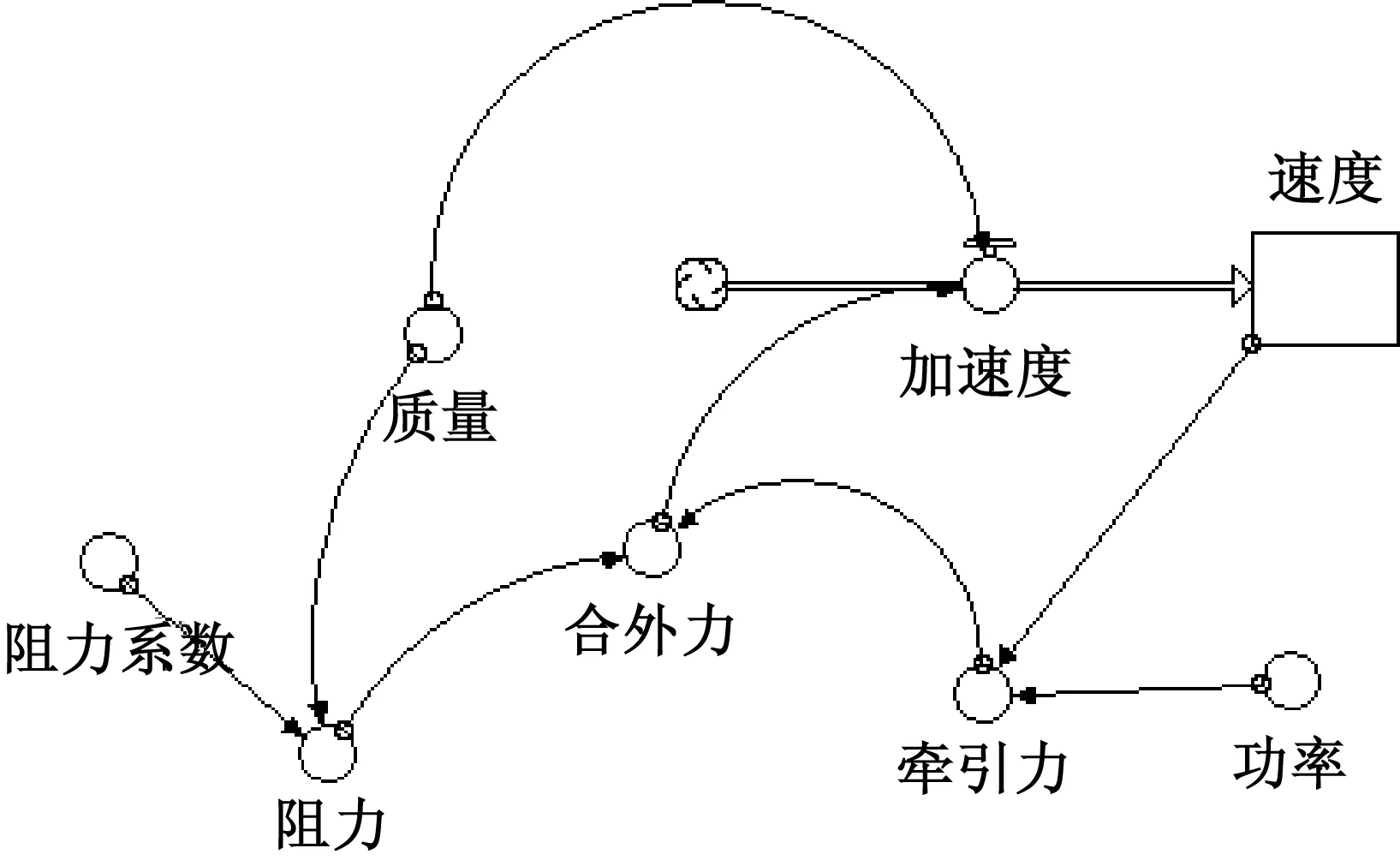
图1

第2步,在Model菜单下,输入已知物理量大小和相关公式．在Equation菜单下,可见系统动力学模型内部公式和物理量大小和关系,如图2所示．

图2

第3步,在Graph 菜单下,建立速度、加速度、牵引力等多个物理量随时间变化规律的图像,在Run菜单下,设置模拟长度等,运行可得如图3,图中1、2、3分别为v-t、a-t、F-t图像．

图3

2 合外力随位移变化的非匀变速直线运动

图4

情景2.如图4,质量为m的小球A穿在绝缘细杆上,杆的倾角为α,小球A带正电,电荷量为q,在杆上B点处固定一个电荷量为Q的正电荷．将A由距B竖直高度为H处无初速释放,小球A下滑过程中电荷量不变,不计A与细杆间的摩擦,整个装置处在真空中．已知静电力常量k和重力加速度g．问:A球如何运动?何时有最大速度?

解析:带电小球A在重力、支持力、库仑力作用下,在斜面上做直线运动,取沿斜面向下为正方向,设两电荷距离为r,由库仑定律和牛顿第二定律,有

初始距离为r0，小球A位移为x,

由于小球A与杆上固定正电荷B点距离r不断变化,导致库仑力大小变化,进而合外力变化,加速度a变化,速度v变化,位移x变化,再导致小球A与杆上固定正电荷B点距离r变化,循环无穷,运动情况比较复杂,属于非匀变速运动．

运用系统动力学方法,应用STELLA软件,建立带电小球多个物理量逻辑关系的系统循环图如图5,这里有两组栈和双向流,左上方一组加速度是流,速度是栈;另一组速度是流,位移是栈．还要特别注意的是,速度、位移、加速度、合力可以为负值．由于题中没有给出物理量大小,在Model菜单下,输入合适的物理量大小数值和相关公式．

图5

图6

在Graph菜单下,创建速度、位移、加速度随时间变化图像;运行展示图像如图6,其中1、2、3分别为v-t图像、x-t图像、a-t图像,可以看出小球沿斜杆做往复运动,是非简谐运动．

3 合外力随速度和位移共同变化的非匀变速直线运动

图7

情景3.一个质量为m、直径为d、电阻为R的金属圆环,在范围很大的磁场中沿竖直方向下落,磁场的分布情况如图7所示,已知磁感应强度竖直方向的分量By的大小只随高度变化,其随高度y变化关系为By=B0(1+ky)(此处k为比例常数,且k>0),其中沿圆环轴线的磁场方向始终竖直向上,在下落过程中金属圆环所在的平面始终保持水平,速度越来越大,最终稳定为某一数值,称为收尾速度,问:金属圆环的收尾速度多大?

解析:磁感应强度竖直方向的分量为By，

By=B0(1+ky).

穿过金属圆环的磁通量为

圆环产生感应电动势和感应电流为

感应电流方向为俯视顺时针方向,大小随速度不断变化．

考虑到水平方向磁场不明,安培力计算比较复杂,通常资料上解法避谈安培力和加速度,考虑金属圆环最终以收尾速度匀速运动,从能量守恒角度,列功率关系等式

学生知道了是什么,但不太清楚为什么．笔者从动力学角度研究．研究安培力和加速度,必须深入研究水平方向磁场,设从圆环中心沿各个方向的磁感应强度水平方向的分量Br．构造一个底面为金属圆环、高为Δy的柱形闭合高斯面,磁通量为0．

可知磁感应强度水平方向的分量Br大小恒定,再由安培力公式

安培力方向竖直向上,对圆环由牛顿第二定律得

分析变加速直线运动过程.

笔者还运用系统动力学方法,建立金属圆环电磁感应诸多物理量的复杂逻辑关系的系统循环图如图8,需要强调的是,速度、位移同时影响电流、安培力、加速度,是双反馈机制．

图8

在Model菜单下,恰当地给相应物理量赋值;在Graph菜单下,创建速度、位移、电路等随时间变化图象;运行图像,如图9中1、2、3分别为v-t图像、y-t图像、y-t图像,充分展示了金属圆环非匀变速直线运动,学生的求知欲和好奇心得到了满足．

图9