基于6DOF的高速射弹入水超空泡特性研究
周梦笛,曹从咏,盛楚倩
(南京理工大学 自动化学院,江苏 南京 210094)
超空泡是指当射弹在水中高速运动时,由于弹体周围的压力急速降低至水蒸气的饱和蒸汽压而使水发生汽化,形成水蒸气泡进而包裹整个弹体的物理现象。超空泡的形成可使得射弹所受的阻力大大减小,从而增加弹体的射程并提高其运动速度。
利用超空泡现象,可以通过提高射弹在水中的运动速度进而使其具有较大杀伤力,其在鱼雷、反鱼雷等武器上都有着广泛的应用。上世纪70年代,前苏联就利用超空泡技术研发了代号为“暴风”的潜载高速鱼雷。我国在超空泡领域的研究起步较晚,现阶段研究大多集中于利用数值求解或进行射弹在水中运动时的外部流场仿真,且射弹模型结构通常过于简化,与实际情况相差较大。李佳川等通过建立子弹纵向运动的动力学模型和分析子弹撞水前后的受力情况对其入水过程进行了数值模拟[1-3];王泽宇模仿风洞工况对带攻角和不带攻角的无尾翼旋转超空泡射弹进行了水下航行的数值模拟[4];胡青青等利用结构网格对水平和垂直两种入水角度下圆柱形射弹水下航行阶段超空泡形态进行了二维数值研究[5-6]。但对带尾翼射弹的入水全过程的三维仿真研究较少,结合工程实际,为了更全面地描述高速射弹入水的超空泡特性,笔者从空泡形态和其发展规律角度入手,利用CFD数值方法,对不同空化器形态的弹体模型在不同入水角下超空泡特性进行模拟,得到4种不同工况下阻力系数和相关速度参数的变化规律,并将仿真得到的弹丸速度曲线与实弹射击中测得的弹丸速度进行对比,论证所设计的仿真模型的可靠性。
1 物理模型
基于实际工程需要,笔者设计了两种口径为3.0 mm具有不同空化器形状的四尾翼反鱼雷射弹模型,如图1、2所示,1#模型采用了锥形空化器,2#模型采用平头形空化器。为了控制变量,两种模型仅在空化器形状上有所差异,其弹长(193 mm)、质量(241 g)和空化器投影面积均一致。
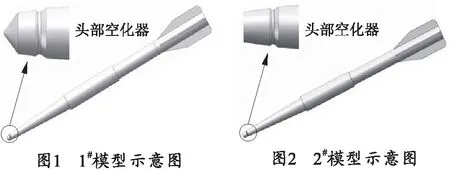
实际工程中射弹的几何形状较为复杂,质量分布不均,且在航行中发生微小形变,笔者为简化弹体模型,作出如下假设:弹丸为理想刚体,在计算中不考虑其形变;弹丸质量分布均匀,且整个弹体为由同一材料构成的实体,弹体密度取实际工程中射弹的平均密度;弹丸在初始时刻攻角为0°;不考虑计算过程中由于弹丸运动而产生的热效应对水蒸汽密度的影响。
2 数值模拟方法
采用基于求解不可压缩粘性流体流动的N-S方程组,利用VOF多相流模型、k-epsilon湍流模型以描述流动,利用6DOF模型定义射弹运动,Schnerr-Sauer空化模型来模拟超空泡的发展及溃灭。Schnerr-Sauer空化模型从汽液净质量传输率的表达式入手,将水和蒸汽的混合物看作是一种包含大量球形蒸汽泡的物质,计算了体积分数:
当Pv>P时:
(1)
当Pv≤P时:
(2)
式中:Re和Rc为传质源相;ρv、ρl和ρ分别为蒸汽密度、液体密度和混合相密度;P为气压;Pv为饱和蒸汽压;α为蒸汽体积分数;RB为空泡直径。
3 网格划分、边界条件及求解设置
基于上述假设,笔者建立了三维模型来模拟射弹入水及超空泡的形成过程,确定弹丸初始位置为弹头距水面约1 cm的高度,弹体用三角形网格进行离散,在弹头处进行网格加密且设立厚度为1 mm的边界层。外围流场形状为四棱柱的压力出口,上方为空气域,下方为水域,由于使用了6DOF动网格,本文的体网格均采取四面体网格,在水面创建加密区以更好地捕捉弹体的入水过程,以入水角60°下的1#模型为例,初始的网格划分及边界条件的设置如图3所示。其中,入水角指的是弹丸头部刚接触水面时,弹体轴线与水平面的夹角。

采用压力基瞬态求解器,设置全局计算域温度为288.16 K,空气域压力为标准大气压,编写UDF文件定义水域压力随深度变化。利用多相流模型和RNG k-epsilon湍流模型,弹体壁面采取标准壁面函数处理。选取基于压力速度耦合的PISO算法求解,该算法相比于SIMPLE算法,耗费内存较大,在一定程度上会延长迭代时间,但可有效减少迭代步数。动量、湍流动能和湍流耗散率采用一阶迎风格式进行离散,压力基分离求解器采用PRESTO!求解。由于6DOF动网格只能在一个cell内使用,初始化之前将外围流场合并,定义空气体积分数为1,通过打补丁的方式定义水域。
4 数值仿真结果分析
笔者借助流体分析软件,并嵌入用户自定义文件,采取上述求解方法,得到了两种不同弹体以1 000 m/s的初速度,分别在入水角为30°和60°工况下超空泡特性及弹体运动变化规律。并且用本文的求解设置建立与实弹射击中相同的工况,将数值仿真的结果与实际射击试验中测得的结果相对比,以验证仿真模型的可靠性。
4.1 空泡形态分析
将数值仿真的结果同经验公式[1]的计算结果进行对比。两种方法计算得到的空炮形态如图4所示,结果整体一致性较好,说明建立的仿真模型具有较高的可靠性。

图5为1#模型在入水角为60°和30°工况下的空泡形态特征图,可以看出,空化器右侧首先触水并使得周围水面向上隆起,隆起高度随入水时间增加,入水初期由于入水角的影响,超空泡呈现不对称形态,空泡左侧略大于右侧,且右侧部分弹体与水接触,随着入水深度的增加,不对称性逐渐消失,右侧空泡进一步发展,呈现光滑,并且逐步包围弹体,水面在尾翼触水的时候再次隆起,趋于平静。

通过观察4种工况下超空泡的形态的变化过程,本次研究发现,半径相同的平头与锥头空化器对超空泡特性影响较小;不同入水角下超空泡的形成过程相似,空泡形态有所差异。在小入水角工况下,空化器与水面冲击时间较长,在水面处的空泡不对称性更强,且直径较大。
4.2 阻力特性分析
阻力系数作为无量纲量,可综合的表达入水角、空化器形状对弹体所受阻力的影响,因此通过仿真试验中监测得到的阻力系数来分析超空泡对弹丸受力的影响。
仿真结果表明,入水角度的变化对弹丸入水后稳定的阻力系数值的影响较小,图6为1#模型在不同入水角度下该参数随时间的变化情况,可以看出,在不同的入水角度下1#模型的阻力系数基本稳定在0.6左右,入水冲击峰值为2.1左右。

在两种工况下,当空化器刚接触水面时阻力系数均瞬间增大,原因在于此时外围流体介质密度发生变化,弹体所受阻力开始由极小的空气阻力转为水阻力,之后的一段时间内该曲线出现了一个较大的峰值。原因在于此时超空泡还未形成,弹体入水部分与水接触,因而存在较大的摩擦阻力及湍流应力,之后超空泡逐渐发展包裹弹体,仅头部空化器与水接触,在这个阶段里,摩擦阻力逐渐减小到接近于0,因此阻力系数也相应的逐渐减小至一个稳定值。但由于存在一定的尾拍扰动,该曲线仍在小范围内上下振荡。当入水角为60°时,与30°的情况不同,在尾翼入水的时候曲线再次出现了峰值,分析原因在于,该时刻尾翼与水面产生了较剧烈的冲撞。通过上节分析可知,当入水角较小时,空化器与水面冲击时间延长,冲击强度相应减小,水面处空泡直径较大,因此小入水角工况下尾翼未与水直接接触。
此外,试验数据表明,空化器形状对阻力系数影响较大,如图7所示。

对比1#模型和2#模型在相同入水角下的阻力系数曲线可发现,两条曲线的变化趋势几乎一致,但2#模型的阻力系数明显大于1#模型,稳定在1.1左右。表1为两种模型在不同入水角度下阻力系数峰值大小,也可观察到2#模型的阻力系数峰值大于1#模型。

表1 两种模型不同入水角下阻力系数峰值表
图8为两种模型在30°入水角工况下入水过程中速度的变化曲线,在初速度一致的情况下,2#模型速度衰减较快,结合两者的阻力系数曲线,可知平头空化器所受阻力大于锥头空化器。

4.3 试验验证
利用模型仿真得到某种实验弹丸速度变化曲线,与实弹射击中测速靶测出的结果进行对比,验证模型的可靠性。如图9所示,通过在指定位置安放测速靶,测得5个点位弹丸的航行速度。可以看出三维模型仿真得到的曲线十分接近于实测值,说明模型仿真得到的弹道和超空泡特性与实际发射结果相接近,可靠性较高。

5 结束语
通过对具有不同空化器形状的高速射弹在不同入水角下的空泡形态和动力特性进行对比分析,主要得到以下结论:
1)仿真结果与经验公式计算结果、实弹射击结果吻合程度较好,仿真成果可靠性较高。
2)本次研究对射弹入水过程进行了三维仿真,考虑了3个平动、3个转动共6个自由度对超空泡特性及入水阻力的影响,可为非静水环境下射弹入水仿真提供参考。
3)对比了两种具有不同空化器形状、相同空化器直径的射弹在不同入水角下的空泡形态特征及阻力特性,可为超空泡射弹的优化设计提供依据。结果表明,两种空化器对超空泡特性的影响较小,平头空化器在入水时阻力系数较大。

