目标立意以生为本教学有序——《用字母表示数》教学思考与实践

徐 宾

一、研究教材的变化，明确目标立意

笔者就《用字母表示数》这一教学内容，首先将2011 版本教材与2001 版教材进行了对比研究，得到了以下启示：

2001 版本：

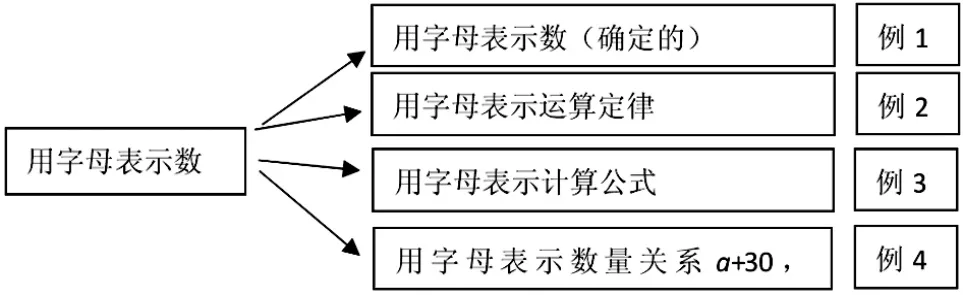
2011 版本：

1.凸显了用字母表示数不确定性的本质。

新教材删除了用字母表示确定的数这一内容，直接用含有字母的式子表示数量关系，凸显用字母表示数的本质——不确定性。

2.增加了用字母表示数量关系的课时数。

新教材增加了用字母表示数量关系的课时数，重点突出用含有字母的式子既表示数量，又表示数量关系。如用a+30 既表示父亲的岁数比女儿的岁数大30 岁的数量关系，又表示父亲的岁数。这是初学时的一个难点，首先学生要把语言叙述这一关系改为用含有字母的式子表示。其次，学生不习惯将a+30 视为一个量，学生常常会认为这是一个式子，不是一个结果。为了突破这个难点，教材增加了用字母表示数量关系的例题和练习，为方程以及用方程解决问题的教学做好铺垫。

二、研究学生的问题，倡导以生为本

1.课前访谈中的问题。

为了了解学生对用字母表示数的真实学情和想法，笔者对五年级3 个班的学生进行了访谈，让学生写一写“看到《用字母表示数》这个课题你想到了什么”。

通过整理，笔者发现学生对这个问题的想法主要体现在：（1）为什么要用字母表示数？用字母表示有什么好处？（2）怎样用字母表示数？用字母可以表示哪些数？哪些数可以用字母表示？通过分析，笔者认为可以用这两个问题引领全课，学生明白了怎么用字母来表示数，学会了用含有字母的式子表示数，并感受到了这种式子的简洁性和概括性，那么这堂课的教学目标也就实现了。

2.课堂教学中的问题。

【案例】：a+30 不是结果！

师：a+30 表示父亲的年龄，也表示父亲比女儿大30 岁。

生：可a+30 到底是几岁呢？这不是结果。

学生的学习存在潜在困难。对字母式只认同是一个运算过程，而不是一个结果。因此，笔者认为第一次出现用字母式表示时要舍得花时间进行强调感悟。如下图，让学生经历感悟到等号左边是计算的过程，而右边则是一个计算的结果。

对于这个难点也不能一蹴而就，教材在后面又增加了这方面的课时，让学生进一步感悟。

3.后续学习中的问题。

在后续学习用方程解决问题中，有些学生经常会出现错误。所以，笔者认为可以在第一次教学用字母表示数时进行适当渗透。

三、研究教学的设计，经历关键步骤

吴正宪老师说：“学生如果想真正走进概念，就必须经历过程。”如何经历过程，理解概念本质，笔者从立序、对比和选材三方面展开思考和实践。

1.经历关键步骤——立序。

“循序渐进”是小学数学教学应该遵循的教学规律。课堂教学要厘清知识内容的“序“，尤其是概念的教学，要经历序的过程。

笔者认为，用字母表示数的教学流程可以这样设计。（1）体会用字母表示数的必要性，体会确定和不确定，不确定下有范围。（2）用字母或字母式可以表示数量。（3）进一步感知，含有字母的式子也可以表示数量关系。（4）深入研究，体会用字母式表示与用字母表示的区别——既可以表示数量，也可以表示数量关系。

2.感悟概括优势——对比。

前苏联教育家乌申斯基说“比较是一切理解和思想的基础”。本堂课笔者认为可以从以下两方面的对比着手。

（1）特殊与一般的对比。

师：今年老师34 岁，胖胖34-30=4（岁），明年老师35 岁，胖胖5 岁，当老师40 岁时，胖胖10 岁。像这样的情况还有很多很多。让我们来观察一下吧！这是今年我们的年龄，这是明年我们的年龄，那a，a-30 这是哪一年我们的年龄？

生：所有年龄都可以。

师：这两个式子能简明地表示出任何一年我们的年龄，那你觉得用字母表示数有什么好处？

小结：看来用字母表示数能表示出所有情况，十分简便。

这一从特殊到一般的对比过程的反馈，其实是让学生经历从个别到一般的归纳过程。其一，通过对比，让学生体会用字母表示数的概括性和简洁性。其二，通过对比，在变与不变的过程中，让学生初步体会函数思想。其三，通过对比，渗透在后续学习用方程解决问题中，当两个有关联的未知量，设一个为x，另一个可以用含有x 的算式来表示的意识。其四，对字母式的含义，既表示数量，又表示数量关系进行及时巩固。

（2）具体与抽象的对比。

师：老师还带来了一盒笔，猜一猜，盒子里面大约有几支笔？

生：30 支，40 支。

师：还可能是几支？

生：可能是100 支。

师：一定是30 支吗？

生：不一定。

师：一定是40 支，100 支吗？

师：刚才老师手中笔的数量是确定的，可以用具体的数5 来表示，现在盒子里面笔的支数不确定了，你们说该表怎么示？

生：x，a，b，m……

师：因为盒子里笔的数量不确定，我们就想到用字母来表示。

师：大家猜测的30 和x 表示盒子里的笔的数量，它们有什么不同呢？

数只能表示一个特定的情况，是确定的。而字母不仅能表示特定一种情况，还能表示一个集合中任意一个值的量，是不确定的。这是两者的本质区别，也是字母表示数的优势所在。在教学中，让学生经历“具体数”与“字母”的对比思辨，从而理解字母或字母式可表示一个集合中的任意数。经过对比、思辨、交流等数学活动，促使学生对概念意义的理解从低水平层次向高水平层次转变。

3.显概念本质——选材。

本堂课的新授环节借助三个盒子，完成新课的教学，让学生经历感悟体验知识的形成过程。

选择材料的理由：

（1）纸箱子不带情境因素，没有附加情境的干扰，从而将学生的思考集中聚焦在对数的表示上。

（2）当学生看见教师往盒子里放笔时，用数表示是明确的，当学生看不见盒子里的笔的数量时，用数表示就是不确定的。在对比中，呈现了本课时内容所要面对的数的状态。这个与其他素材等所带来的兴趣是有本质不同的。

（3）通过比较两个纸盒y 与x+5 谁更合理，引出字母式的优越性，揭示概念本质。

四、再思考，再出发

通过教学实践及反思，笔者认为要让学生真正感悟用字母表示数的本质，我们还有很多问题值得思考和实践。

1.如何创新？如何基于学生的真实学情设计教学？

2.如何加强衔接，从整体上体现用字母表示数的教学价值？

3.如何让学生体会到a+30 是一个结果，我们可以怎么做？

帮助学生实现从具体、真实的数字向抽象的字母的认知转变,形成抽象意识和符号意识。