基于粗糙集理论的高校教师评价体系研究*

付沙 肖叶枝 周航军

（湖南财政经济学院 湖南长沙 410205）

一、引言

高校教师评价体系是对高校教师教学、科研以及师德师风等一系列工作的量化评价。随着近年来高校教师人事、绩效制度的进一步深化改革，各高校在人才引进、职称晋升以及绩效考核等问题正不断融入更多的竞争与择优机制。为确保全面提高教育教学质量、教师素养，促进学校管理更加科学化，优化学校人力组合，必须进一步加强教学评价工作的深入落实与完善。对此，探索建立一套符合高等教育办学与人才培养规律，促进教师职业发展的教师评价体系是当前亟待解决的首要问题。为完善多元化的人才评价标准，构建科学、合理、高效的评价体系与比较方法是教师评价工作的关键所在。

美国学者Nolan[1]将教师评价认定为一种组织能力，可通过对教师行为与能力的综合判断对人员的聘用以及连续任用做出决策。Elsa Cardos等学者通过整合高校效力与效率项目的决策支持系统，运用平衡记分卡建立了高校教师绩效评价体系。英国对教师专业标准不断地进行修订、完善，颁布了《英国教师专业标准》，从专业素质、专业知识和理解、专业技能三个维度做出具体规定。美国加州大学伯克利分校制定了关于教师教学评价的相关政策，该政策指出教师的教学评价必须要以证据为基础，务必做到有证可查、有据可循。这一系列研究成果为国内教师评价体系研究提供了较为完善的理论框架和研究方法。与国外的研究情况相比，国内的研究起步则相对较晚。胡涛[2]以郑州大学为例，对“双一流”背景下高校教师教学发展与评价体系进行了研究和探讨；李建林[3]运用粗糙集理论进行数据分析和处理，对教师教学质量评价系统原始数据的属性约简和权重确定，评价更为客观、有效；蔺洪全[4]针对当前高校教师考核评价中存在的问题，结合理论分析和实例，基于师德、教学、科研、人才培养、学科建设、社会服务六个方面构建了高校教师考核指标体系；韩小林[5]采用分类的方法构建指标体系，从分型的角度设定指标的权重，对高校教师进行分层次、全方位的评价研究。

由当前国内高校教师评价的现状来看，大部分评价体系缺乏完整性和连续性，也没有充分考虑高校教师这一群体的复杂性和特殊性，致使评价工作多流于形式，未能达到理想效果。此外，目前的教师评价大多采用由学生、同行、领导以及专家评价相结合的方法获取单纯的定量评价结果；或采用加权平均法实施量化考评，这种做法在很大程度上受到决策者先验知识的影响，其决策规则和推理过程的有效性受局限，其结果较难对教师做出客观评价，也不能充分发挥评价工作对教师教学、科研的导向作用[6]。本文以提高高校教师教学水平与科研能力，促进其多维度、全方面发展为目的，运用粗糙集理论与信息熵实施教师评价指标分析，不仅可以有效地分析高校教师能力评价中各种精确性、完整性和一致性的信息，而且可以对数据进行分析和推断，挖掘隐性知识，揭示潜在规律。

二、理论基础

（一）信息熵理论

熵理论由德国物理学家Clausius在1865年首次提出。1948年，Shannon将熵的概念引入信息领域，利用信息熵衡量信息的混乱程度，提出了信息的量化度量方法

利用熵来测量随机事件的不确定性或信息量，通过概率和统计的方法，为现代信息论提供了科学的理论基础，对熵的量化应用予以大幅扩展，并应用于系统的各项定量研究中。

（二）粗糙集方法及相关理论

二十世纪八十年代，波兰数学家Pawlak创立了一种用来处理模糊、不确定知识的数据处理方法——粗糙集理论。该理论主要使用已知的知识库来描述知识库中的不准确或不确定性知识，因为它不需要提供除了问题所需处理的数据集之外的任何先验信息，所以不确定性的描述和处理更加客观。

与文中研究相关的几个粗糙集概念及定义如下：

定义 1：设S=(U,A,V,f )是一个决策表，其中，是对象的非空、有限集合，也称为论域；A是属性的非空、有限集合，A的具体内容可以描述为：其中，C表示条件属性集,C表示决策属性。V为属性值域，V的具体内容可以描述为：其中，Va是属性a的值集；是一个映射，它为每个对象的属性分配一个信息值。

定义 3：从概率论方向上来说，公式S=(U,A,V,f )为一个随机系统，假设X为非空有限论域U上的随机变量, X={X1，X2，... , Xn} ,则其概率测度分布可以确定：

定义 4：从信息论的角度，设S=(U,V,A,f )为一个信息系统,U|A={X1,X2,...Xn},引入信息熵理论中的熵函数，则A的信息熵为：

定义 5： 在决策表S中， 若U|IND(C)={X1,X2,...,Xq},U|IND(D)={Y1,Y2,...,Yp},则对象集U在条件属性集C下相对于决策属性D划分的信息熵可定义为：

三、基于粗糙集和信息熵的综合评价模型

（一）问题描述

本研究将粗糙集和信息熵引入高校教师评价，建立综合评价模型。高校教师评价体系包含4个一级指标、13个二级指标的属性集合，对决策表S内的属性集C作如下描述：C={C1,C2,...,CZ} ，关于一级指标条件属性CX(x=1,2,...,z),均包含了若干个二级指标条件属性，可表述为CX={CX1,CX2,...CN}[7]。

首先，需要对连续数据给予离散化操作，再将离散化的结果转换为决表S=(U,A,V,f),U={u1,u2,...,un}表示各评价对象的集合，条件属性集C={C1,C2,...,CZ}，决策属性集D={d1,d2,...dk}

（二）模型的评价步骤

此研究所要探讨的是考虑粗糙集和信息熵的智能评价模型，首先，利用决策表S完成数据记录，再依次计算属性权重值w以及综合评价值Ei[8]。步骤如下：

步骤1：计算全体对象集U的划分结果U|IND(C)，在属性上的划分结果U|IND(D),以及筛选掉各属性D后的划分结果U|IND(C-{CX})；

步骤2：计算属性集C对应决策属性D的信息熵I(D|C)；将属性集进行分别筛选各属性CX后，计算C-{CX}对应于D的信息熵I(D|C-{CX})；

步骤3：针对各属性CX，计算粗糙集理论下的相对重要度：

步骤4：从信息熵的角度计算各评价指标的客观权重值：

步骤5：由定义7计算各属性的知识熵：

依据各属性的知识熵大小确定权重分配，即对知识熵进行归一化处理，得到各属性主观权重w。

步骤7：计算评价对象的综合评价结果。

四、实例分析

运用专家咨询和文献调研等方法，建立具有多元化评价标准的评价体系。主要评价指标包括：基本素质和道德评价、教育教学评价、科学研究评价、服务社会的能力与贡献评价，其核心维度的规模满足现当代高校教师评价体系的发展趋势[9]，如下图所示。

以某省属重点大学在岗教师评价为例，邀请该领域的专家、教授组成专家小组，选择该高校若干名教师的多项指标进行综合评价。考虑到粗糙集仅能处理离散数据，论文选取等距离方法对连续数据进行离散化操作。受篇幅所限，只罗列初始信息经离散化处理后的结果，如表1所示。

表1 数据经离散化处理后的决策表

（1）计算C1分块下各二级指标C1n（n=1,2,3)在粗糙集理论体系中的相对重要度SGF({C1n})。

（2）计算C1分块下各二级指标C1n的相对权重值(C1n)。

同理，计算一级指标C2、C3、C4分块下的各项数据，限于篇幅，其余评价指标权重的计算过程及数值不再赘述。

（3）以属性C11为例，其数据离散化后的决策表划分U|IND(C11)={{1,2,3,5,7,9},{4,6},{8,10}}，知识熵为：H(C11)=0.56

同理，计算C12和C13的知识熵分别为：0.56、0.58。

根据各属性的知识熵大小确定权重分配，得到各属性主观权重为：

限于篇幅，其余评价指标权重的计算过程及数值不再赘述。

（4）经过研究选取主观因子µ= 0 . 4 ，由公式(9)计算各评价指标的综合权重为：

w(C11)=0.242，w(C12)=0.376，w(C13)=0.381

w(C21)=0.299，w(C22)=0.172，w(C23)=0.186，w(C24)=0.169，w(C25)=0.174

w(C31)=0.339，w(C32)=0.371，w(C33)=0.290

w(C41)=0.570，w(C42)=0.430

（5）根据信息熵观点下的粗糙集方法，计算一级指标的权重值。

w(C1)=0.245，w(C2)=0.295，w(C3)=0.308，w(C4)=0.152

结合二级与一级指标权重，得到全局情况下二级指标的综合权重值。

w(C11)=0.059，w(C12)=0.092，w(C13)=0.093

w(C21)=0.088，w(C22)=0.051，w(C23)=0.055，w(C24)=0.050，w(C25)=0.051

w(C31)=0.104，w(C32)=0.114，w(C24)=0.089

w(C41)=0.087，w(C42)=0.065

（6）依据文中算法，计算得到上述10位教师的综合评价结果，具体结果及排序如表2所示。

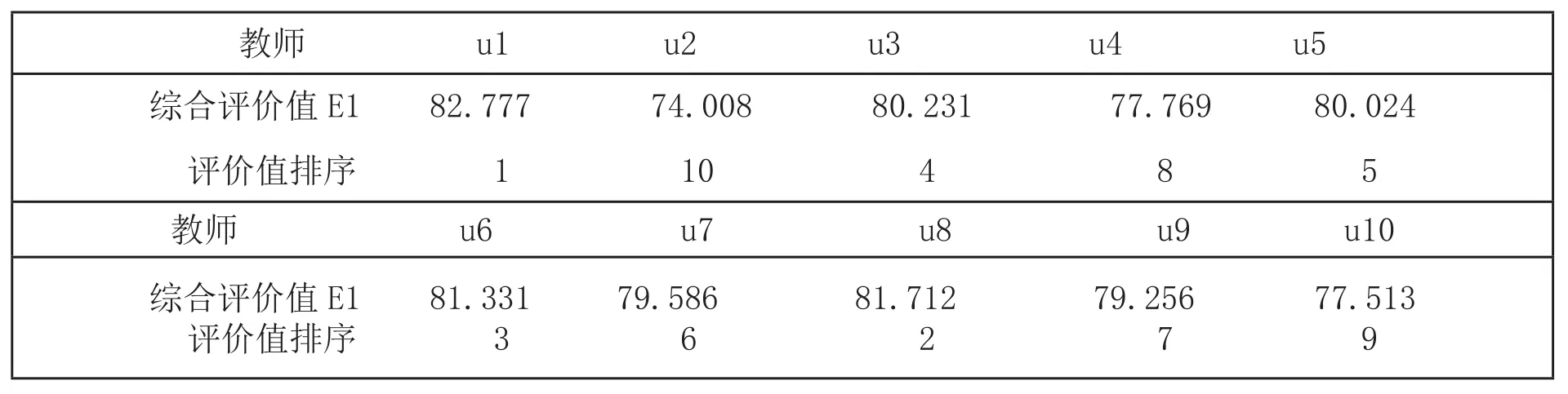
表2 综合评价结果及排序

综合评价结果与已有的考核结论符合性较高，验证了该评价模型在一定程度上能够客观有效地反映参评教师的实际绩效情况。

五、结语

作为高校管理的重要内容以及相关制度的制定依据，高校教师评价已成为当前的研究热点。本文重点研究了高校教师评价体系中指标及其权重的确定，充分考虑影响高校教师评价结果的因素，建立了切实可行的、有效的评价体系。为了能够使评价决策结论进一步地全面化与客观化，通过将粗糙集理论和信息熵引入到评价分析中来，对决策表进行分块解构，以层次式计算的方式获取属性客观权重；通过分析属性知识熵和权重之间的联系，结合基于知识熵的权重确定方法，对教师各方面能力进行更为客观、有效的评价。该评价体系可促进高校建设和改革，促使教师个人能力的提升，增强学校的竞争力，其研究亦为高校教师评价提供了一种新的思路和途径。