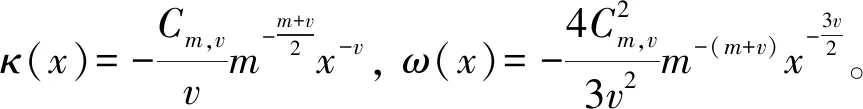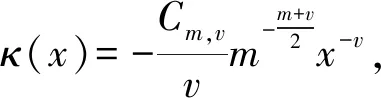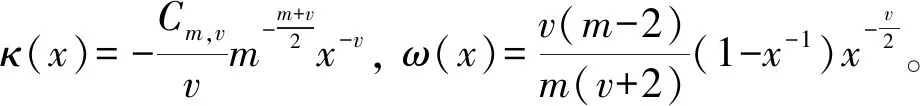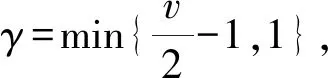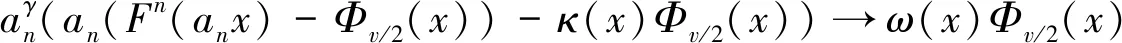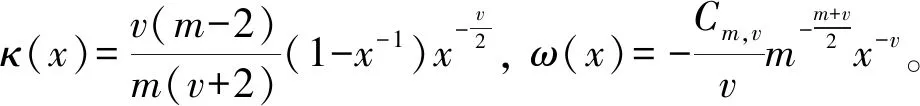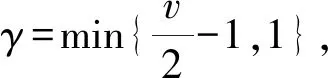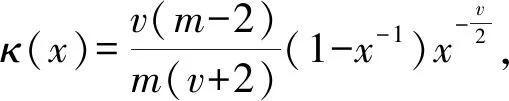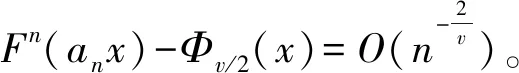费希尔分布最大值分布的渐近展开
韦 杰,曾 萍
(贵州中医药大学 信息工程学院, 贵阳 550025)
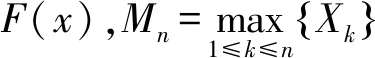
(1)
其中G(x)为非退化分布函数。若上式在G(x)的连续点处成立,则称F(x)属于G(x)的吸引场,记作F∈Dl(G),并且G(x)只能是3种经典极值分布类型之一[1]。自极值理论提出后,学者们对其展开了深入的研究[2-8]。在抽样分布中,费希尔分布的概率密度函数[9]为

(2)
其中m、v表示自由度(m>0,v>0),
本文主要研究在最优规范化常数条件下,自由度为m、v的费希尔分布随机变量序列最大值分布的渐近展开,并得到最大值分布收敛到极值分布的逐点收敛速度。
1 相关引理
为了证明定理,需要一些辅助引理。首先给出费希尔分布尾部表达式、Mills率和最优规范条件下最大值的极值分布。
引理1设f(x)和F(x)分别为费希尔分布概率密度函数和分布函数,对于充分大的x>0,有
(3)
证明对于x>0,有
(4)
由洛必达法则得到
(5)
结合式(4)(5),对于充分大的x可以得到式(3),引理得证。
引理2当x→∞时,有Mills率:
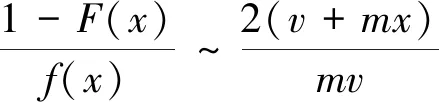
(6)
证明对于x>0,由引理1可得
综上,当x→∞时,引理得证。
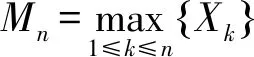
其中,规范化常数
(7)
证明对于引理1,当x>0时,有
根据引理1和文献[1]的推论1.12得到F∈Dl(Φv/2)。存在tn,使得满足n(1-F(tn))=1,因此结合式(6),当n→∞时,有
整理得到
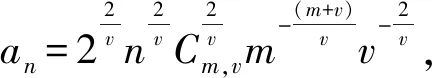
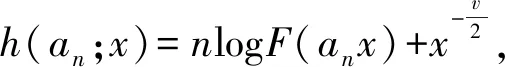
1) 当0 2) 当v=1时,有 3) 当1 4) 当v=2时,有 an(anh(an;x)-κ(x))→ω(x) 其中,这几种情况的κ(x)和ω(x)在定理1中给出。 证明令 (8) (9) (10) (11) 下面讨论0 类似可得 引理得证。 定理1设{Xn,n≥1}为i.i.d.序列,F(x)为费希尔分布的分布函数,规范常数an由式(7)给出,当n→∞时, 1) 当0 (12) 2) 当v=1时,有 (13) 3) 当1 (14) 4) 当v=2时,有 (15) 其中: (16) (17) 证明由引理3可知,当n→∞时,h(an;x)→0且 (18) 下面讨论0 定理得证。 致谢:衷心感谢西南大学彭作祥教授在学术科研上的悉心指导。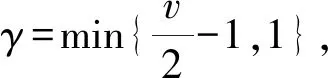
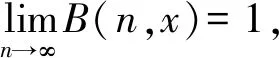
2 主要结论