基于离散时间观测带有马尔可夫切换的随机网络系统的反馈控制

叶志勇，王泽权，唐朝君，匡 艳

(重庆理工大学 理学院， 重庆 400054)

随着网络通信、控制和计算技术之间的相互渗透和发展，网络系统已经广泛应用于各个领域之中。作为科学和工程控制领域的新兴学科，网络系统一直受到广大研究者的关注，并且网络系统在物理学、计算机科学、生物学等也有着广泛的应用[1-7]。

近20年来，学者们对随机微分方程的稳定性的控制问题已进行了广泛深入的研究，取得了很多优秀的成果[8-12]。文献[13]指出：如果给定的随机微分方程是不稳定的，则可以通过设计一个反馈控制μ(x(t),r(t),t)使其达到稳定状态。然而这种有规律的反馈控制要求在所有的时间上对状态进行连续观测，在经济上这种方法是非常昂贵的，实际上连续情况的观测也可能无法实现。所以毛学容等[14]提出了基于离散时间状态观测的随机微分方程的反馈控制问题，即在离散时间观测的基础上设计一个反馈控制μ(x([t/τ]τ),r(t),t)，使其控制更加合理和实用。毛学荣等[14]设计了几类重要的随机微分方程基于离散时间观测的反馈控制器。

在实际中，网络本身在某个时刻会受到不可预料的外部或者内部扰动，这是无法避免的。所以，本文讨论的是带有马尔可夫切换的随机网络系统基于离散时间观测的一致性问题，通过使用普希茨条件，直接研究基于离散时间观测的反馈控制系统本身，对τ建立一个更好的上界，得到了带有马尔可夫切换的随机网络系统稳定性的条件，使网络系统的各个节点达到同步。

1 基础知识和模型建立

1.1 符号说明

1.2 模型描述

考虑带有N个节点的复杂网络，每个节点的动力学系统可表示为如下系统：

dxi(t)=f(xi(t),r(t),t)dt+

g(xi(t),r(t),t)dB(t)

(1)

其中初始值x(0)=x0∈Rn，r(0)=r0∈S，xi(t)∈Rn(i=1,2,…,N)，f∶Rn×S×R+→Rn，g∶Rn×S×R+→Rn×m。r(t)是t≥0时概率空间上右连续的马尔科夫链，取值为有限的状态空间S={1,2，…，N}，生成元为Γ=(γij)N×N。当θ>0时，从时间t在模态i到时间t+θ在模态j的转移概率为：

P{r(t+θ)=j|r(t)=i}=

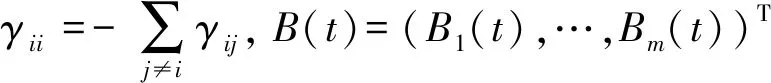
现在设计一个基于离散时间状态的反馈控制μi(x([t/τ]τ),r(t),t)，使各个节点在方程(2)下趋于同步。方程(2)如下：

dxi(t)=(f(xi(t),r(t),t)+

μi(x([t/τ]τ),r(t),t))dt+

g(xi(t),r(t),t)dB(t)

(2)

令ξ=(ξ1,ξ2,…,ξn)T是Laplacian矩阵L的左特征向量，特征值为0，ξT1=1。因为ξTL=0,所以有

(3)

同时，令

(4)

为了方便讨论，接下来引入一些假设、定义及引理。

定义1(伊藤(It)公式)[15]首先考虑一个随机微分方程：

dx(t)=f(t)dt+g(t)dB(t)

其中：t≥0，f(t)∈L1(R+,Rn)，g(t)∈L2(R+,Rn×m)，V(x,t)∈D2,1(Rn×R+,R)。定义在Rn×R+→R上的极小生成元LV：

LV=Vt(x,t,i)+Vx(x,t,i)f(t)+

(5)

其中：

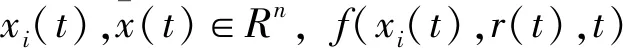
(6)

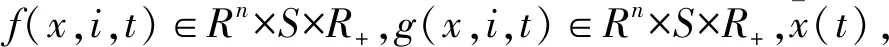
2 主要结论

为了解决方程(2)的稳定性问题，将反馈控制设置成：

(7)

其中xi, j(t)=xi(t)-xj(t)，i,j∈V，μ∈R。

随机微分方程(2)通过式(4)和(7)写成如下：

(8)

接下来是证明方程(8)稳定性的主要理论。

引理1当τ>0，令

(9)

如果τ(τ≥0)足够小并且满足2K(τ)<1，则随机微分方程(8)中的xi(t)的解满足

(10)

证明存在一个整数v≥0，t∈[vτ,(v+1)τ)，令δ(t)=vτ，根据方程(8)可得

得到

然后利用格朗沃尔不等式得：

所以当t∈[vτ,(v+1)τ)时方程(10)成立。

定理1如果满足下面的不等式：

(11)

ξmax=max{ξ1,ξ2,…,ξn}

语言中的绝大多数词都拥有多个意义。传统的语义研究没有认识到多义词各个义项之间的内在联系，没有对语义扩展的机制做出合理的解释。认知语言学揭示了多义现象的本质，认为词的多个意义中除了基本义之外，其他意义是通过隐喻和转喻的方式由基本义扩展而来的。雷可夫指出，一词多义起源于不同认知域之间以及同一认知域中不同元素之间的关系。词的基本义与扩展义之间有直接的认知性关系。词的各义项之间存在着理据性关系是因为词义的扩展从主观上来说主要是通过隐喻和转喻思维来实现的。词义扩展的方式主要有两种:基于与中心义的相似性关系派生新义为词义的隐喻性扩展，基于与中心义的邻近关系派生新义为词义的转喻性扩展。

λ1=max{(LTL)⊗In}

λ2={(ξL)⊗In}

则基于离散时间观测带有马尔可夫切换的随机微分方程(8)是稳定的。

证明首先建立一个适当的Lyapunov泛函方程

(12)

利用伊藤公式得到随机微分方程(8)的极小生成元如下:

(13)

通过方程(13)得：

(14)

同理：

(15)

将方程(9)(15)代入到方程(13)得：

(16)

(17)

同时，通过伊藤公式[18]得:

(18)

将式(17)代入到式(18)得：

(19)

由式(19)得Ω<0，所以方程(11)是稳定的。

3 实验仿真

本文考虑的是一个随机混杂系统

dx(t)=[A(r(t))x(t)+C(r(t))G(r(t))x(δ(t))]dt+

B(r(t))x(t)dB(t)

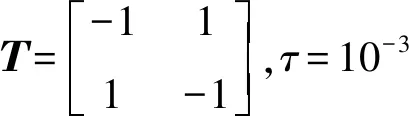
根据定理1，借助Matlab求得可行的解为：

G1=(1,0)，G2=(0,1)

根据实验的仿真结果，利用Matlab绘制随机切换和状态响应图，见图1～3。

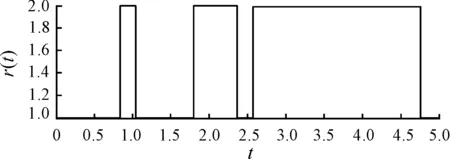
图1 随机切换

图2 状态响应1

图3 状态响应2

图1表示在r(0)=1的马尔可夫链切换的一种可能状态，图2、图3显示的是在给定的初始值x1(0)=-2和x2(0)=1以及离散时间τ=10-3条件下的响应状态，可以看出所考虑的系统在相应的条件下最终可以达到稳定。

4 结束语

本文研究的是基于离散时间观察并带有马尔可夫切换的网络系统模型，通过建立李雅普诺夫泛函方程，计算网络系统的极小生成元，得到基于离散时间观测稳定性的充分条件，把系统的稳定性问题转换为线性矩阵不等式的问题。同时可以将本文方法应用到多智能体系统中，讨论在离散时间状态下的多智能体分布式反馈控制。最后，对本文的结果进行数值模拟，验证了结果的正确性和有效性。