非稳态油膜力对转子系统盘轴松动故障的影响研究
刘 杰 , 李志农, 卢文秀
(1. 南昌航空大学 无损检测技术教育部重点实验室, 南昌 330063; 2. 清华大学 机械工程系, 北京 100084)
松动故障是旋转机械的常见故障之一,国内外学者对其进行了大量的研究,形成了较为完整的体系。Chu等[1-2]对基础松动故障转子系统的振动特性、频率特性、周期运动、混沌运动等方面进行了详尽的理论和实验研究;张靖等[3-4]针对两端支座同时松动的转子系统,建立了带有贴合工程实际的非稳态油膜力的非线性微分方程组,利用龙格库塔法进行求解,分析了系统的振动特性和频率特性。Lu等[5]建立了松动-碰摩耦合故障有限元力学模型,分析了不同松动刚度及不同摩擦间隙对整个系统的振动影响。刘长利等[6]重点讨论了偏心量、裂纹深度及其它因素对松动裂纹耦合故障转子系统的分叉和稳定性的影响。王宗勇等[7-9]针对离心机这种转子质量具有慢变特性的旋转机械,假设转子质量以余弦规律缓慢变化,建立了具有质量慢变特性的松动故障转子系统、松动碰摩耦合故障转子系统非线性运动微分方程组,采用4阶龙格库塔数值法求解,分析了转动频率、质量慢变系数对故障系统动力学特性的影响。然而,目前的研究主要集中在非转动部件的松动故障,关于盘轴松动故障的研究却忽略了。当转盘和转轴存在间隙时,油膜涡动会影响转轴的运动轨迹,进而影响盘轴碰摩;而盘轴的碰摩又会对油膜涡动造成很大的扰动。盘轴碰摩与油膜涡动之间的互相影响会对整个转子系统的动力学特性造成影响。因此油膜力对转子系统盘轴松动故障的影响具有重要研究价值。
伊朗学者Behzad在盘轴松动方面进行了初步的探索,在文献 [10-11]中,采用线性油膜力,假设转盘以一个恒定速度旋转且盘轴总是处于接触状态的前提下建立了盘轴松动模型,并研究了不同圆盘转速对转子非线性动力学行为的影响。显然线性油膜力模型对于盘轴松动故障的研究不够精确,忽略了盘轴存在间隙时的碰摩运动也会影响仿真结果的精确性。因此有必要建立合理的油膜力模型和盘轴碰摩模型。
文献[12-13]提出的非稳态非线性油膜力模型有效的解决了扰动对油膜的影响,并且文献[3-4,14-15]采用此模型取得了较好的研究成果,这些成果的取得给盘轴松动故障中考虑油膜涡动的影响提供了重要参考,在此,本文采用此油膜力模型。基于此,本文首先采用Hertz接触理论建立了盘轴碰摩模型,利用四阶龙格-库塔法对运动微分方程进行数值仿真,然后,讨论非稳态油膜力对转盘转动状态的影响及油膜间隙对转子系统振动特性的影响,为盘轴松动故障建模及动力学特性分析提供重要的参考。
1 数学模型
1.1 基于Hertz接触理论的碰摩模型
盘轴系统碰摩模型如图1所示,o1为转轴的形心,坐标为(x1,y1),o2为转盘的形心,坐标为(x2,y2),c为转盘质心,θ为转盘的转动角位移。Fr、Ft为转盘对转轴的径向力与切向摩擦力。

图1 盘轴系统碰摩模型
为简化研究,这里,作如下假设[16]
(1) 盘、轴碰摩过程中转盘整体保持刚性,转轴保持刚性,两者接触时的几何关系按内切圆处理,因此相互碰撞力在二者的公法线上,为径向力Fr;
(2) 盘、轴碰摩过程中仅在挤压接触区域有局部弹性变形,忽略挤压过程中的阻尼效应;
(3) 盘轴接触过程符合库仑摩擦定律条件,若接触点处摩擦因数μ,则切向摩擦力为Ft=μFr。
将转盘和转轴分别看成为有一定厚度、宽度的圆盘和圆孔,在这样几何条件下盘、轴碰撞问题简化为二个圆的内接触问题,根据Hertz接触定律,两个弹性体碰撞引起的法向碰撞力
(1)
式中,δ是径向嵌入深度,α为结构常量,表达式为[17]
(2)
式中,νi,Ei,Ri(i=1,2)分别为轴和转盘的泊松比、杨氏模量和撞击局部表面曲率半径。因为盘轴半径间隙h远远小于R1,所以α可记为
(3)
在盘轴的整个碰摩过程中,两者间的径向相互作用力Fr可简要表达为如下非线性形式
(4)

在盘轴接触点处,转轴的切向速度可表示为
(5)
转盘的切向速度可表示为
(6)
令ΔV=Vt1-Vt2,则Ft可表示成如下形式
Ft=sgn(ΔV)μFr
(7)
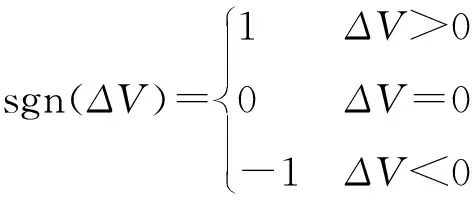
转盘对转轴的作用力在两个坐标轴方向上的分量为
(8)
1.2 盘轴松动故障转子-轴承系统运动方程
如图2所示,采用集中质量、两端滑动轴承支承的转子模型,由简单转轴、松动转盘和滑动轴承三部分组成。m1为转轴在左端轴承处的集中质量,o1是转轴左端几何中心,坐标为(x1,y1);m2为转轴在中间处的集中质量,o2是转轴在中间处的几何中心,坐标为(x2,y2);m4为转轴在右端轴承处的集中质量,o4是转轴右端几何中心,坐标为(x4,y4);m3是转盘的质量,o3为转盘的几何中心,坐标为(x3,y3),因盘轴之间存在间隙h,所以o2、o3并不一定重合。两端采用相同的圆柱短轴承,其参数L、R1、δ1分别为轴承宽度、轴截面半径、轴颈与轴承的间隙。设F1x、F1y、F4x、F4y分别为转轴左右两端受到的油膜力在x、y方向的分量,其表达式见文献[18-19]。由Behzad[17]的研究可知,陀螺效应对盘轴松动系统动力响应的影响较小,为简化研究,忽略陀螺效应。
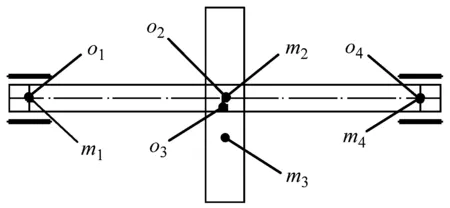
图2 盘轴松动故障转子-轴承系统模型
转轴左端的振动方程为
(9)
式中,c、k分别为转轴的阻尼系数和刚度系数。
转轴中间处的振动方程为
(10)
式中:e2为m2的偏心距;ω为转轴的自转速度;g为重力加速度;F2x、F2y为其受到的碰摩力在x、y方向的分量。
转盘的振动方程为
(11)
式中,c3、e3、θ分别为转盘的阻尼系数、偏心距和转动位移。
转盘的转动振动方程为
(12)
式中,J、cθ、R3、Ft分别转盘的转动惯量、转动阻尼系数、内圆半径和转盘受到的切向摩擦力。
转轴右端的振动方程为
(13)
为计算分析方便,对式(9)、(10)、(11)、(12)、(13)进行无量纲化处理。
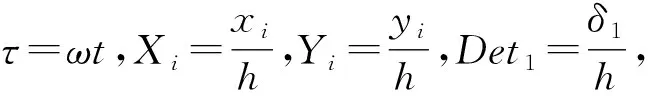
则无量纲化后的运动方程为
(14)
2 数值仿真
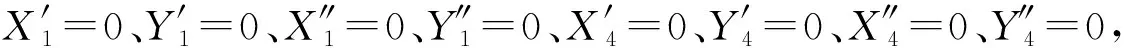
2.1 两种支撑情况下转盘的运动状态对比
在轴承无量纲间隙Det1=10,转轴无量纲转速从低到高仿真发现:这两种支撑情况下,转盘无量纲转速θ′有高低两种状态;不考虑油膜力的转子系统转盘无量纲转速θ′在Ω<0.8时,处于低转速状态,在Ω≥0.8时处于高转速状态;考虑油膜力的转子系统无量纲转速θ′在Ω<1.3时,处于低转速状态,在Ω≥1.3时处于高转速状态;不考虑油膜力的转子系统转盘无量纲转速θ′更早的进入高转速状态。如图3、图4所示为不同转轴无量纲转速Ω,转盘无量纲转速θ′变化图。

(a) Ω=0.5
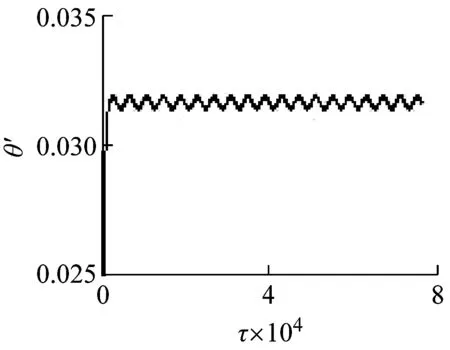
(a) Ω=0.5
2.2 不同油膜间隙情况下的振动特性分析
在转轴无量纲转速Ω=1.5的情况下,对油膜无量纲间隙Det1从小到大进行仿真,对比分析轴承端和转轴中心的运动轨迹和频率特性。
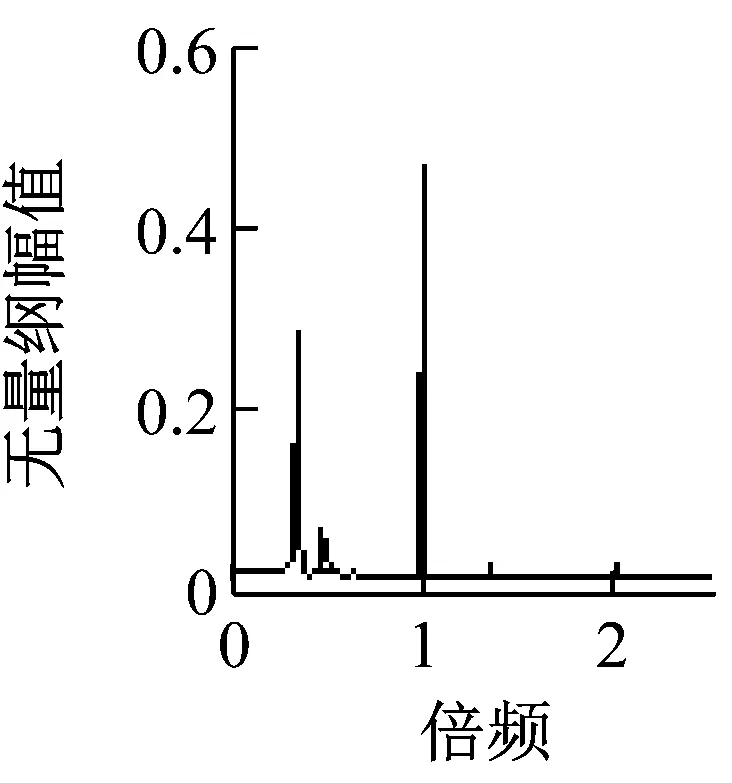
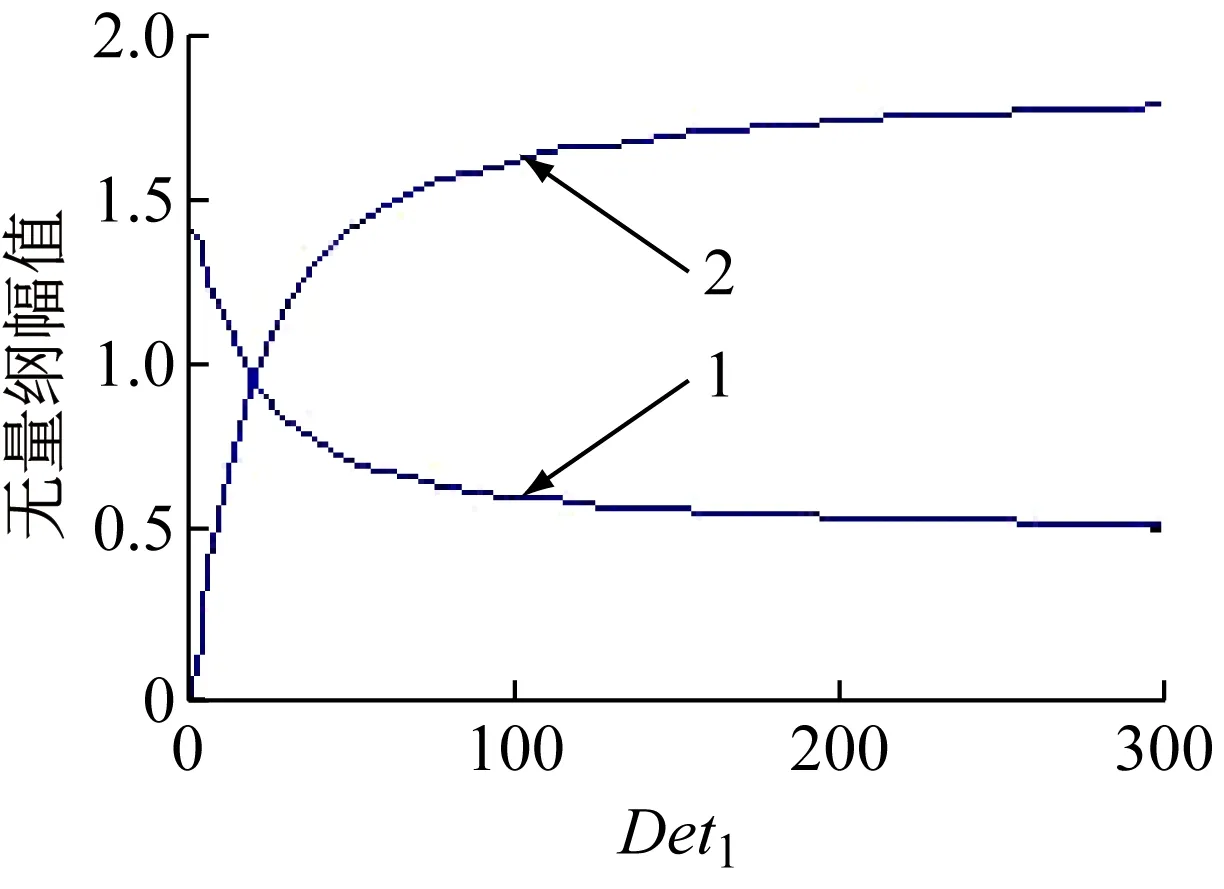
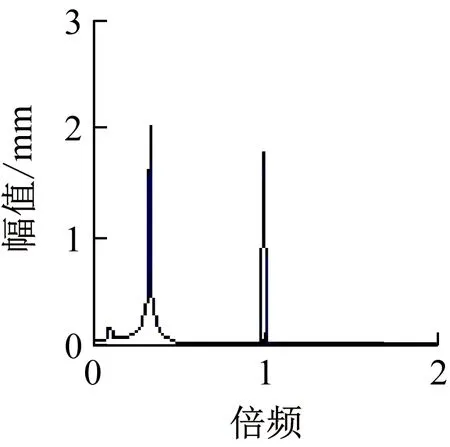
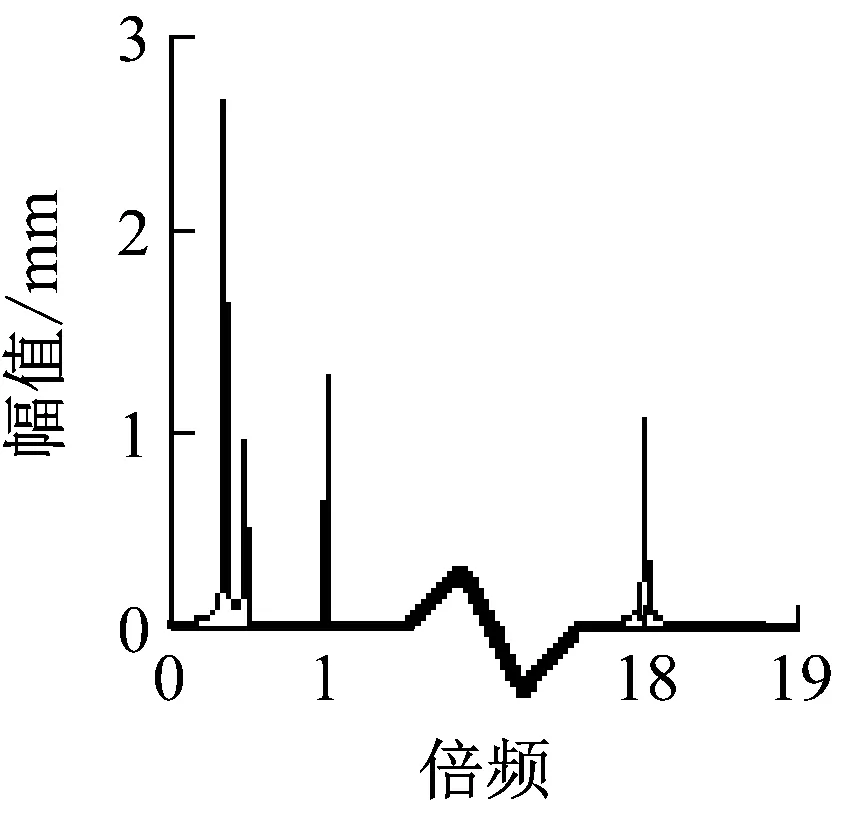
先来看轴承端o1的运动轨迹及X1的频率成分变化。通过仿真发现:当0 (a) Det1=3 X1 频谱图 (c) Det1=9 X1 频谱图 (c) Det1=280 X1 频谱图 再来看转轴中心o2的运动轨迹及X2的频率成分变化。通过仿真发现:o2的运动轨迹像一个不断旋转的扇形,随Det1的变化,并无明显规律。X2的频率成分主要由0.35倍频、1倍频和特别高的63.5倍频组成,分别对应转盘转动频率和转轴转动频率和盘轴碰撞频率,有时还会出现微弱的低倍频。如图6所示为Det1=8时,o2的运动轨迹及X2的频谱图。 由以上的频率分析可以看到,X1和X2都无明显的油膜涡动频率出现,这是因为盘轴碰摩力给油膜涡动造成很大的扰动,使其无法按照一定的频率运动,由o1、o2的运动轨迹图也可以看出o1、o2无周期运动。 (a) o2轨迹图 (b) X2 频谱图 最后分析,各种频率成分谐波的幅值变化情况。由图7可知,转盘转动频率谐波幅值在轴承处和转轴中心处的变化基本一致,当Det1较小时,幅值先急速上升,后急速下降,当Det1较大时逐渐处于平稳状态。由图8可知,转轴转动频率谐波幅值在轴承处和转轴中心处的变化相反,当Det1较小时,轴承处幅值急速上升,而转轴中心处幅值急速下降,当Det1较大时都逐渐处于平稳状态。由图9可知,高倍频谐波幅值在1.6~2.5间来回波动。 为验证仿真结果的合理性,本小节设计了盘轴松动故障转子系统实验。该实验系统由ZT-3转子实验台、本特利电涡流位移传感器和MULLER-BBM采集系统四部分组成。 如图10所示为ZT-3转子试验台,图11所示为ZT-3转子试验台示意图。该实验台由动力输出系统、盘轴松动故障转子系统两部分组成。以挠性联轴器为分界点,右半部分为动力输出系统,由电机、联轴节、转轴、轴承座、键相器、挠性联轴节组成,挠性联轴器右边连接的是一根320 mm的转轴,左边连接的是一根500 mm的转轴,转轴的两端都是由滑动轴承支撑的。挠性联轴器的主要作用是使动力输出系统只输出转矩,而不输出横向或纵向的振动,从而保证盘轴松动故障转子系统实验结果的精确性。试验台中的电机为直流电动机,其输出功率为250 W,通过调速器可以实现0~10 000 r/min范围内无极调速;左半部分为大间隙盘轴松动故障转子系统,由转轴、转盘、轴承座组成。转轴的直径是9.5 mm,转盘的质量为0.612 kg,转盘的外径为76.2 mm,两轴承座中心之间的距离为422 mm。 (1-轴承处; 2-转轴中心处) (1-轴承处; 2-转轴中心处) 图9 高倍频谐波幅值随Det1变化图 图10 ZT-3转子试验台 图11 ZT-3转子试验台示意图 图12为转盘松动结构图,盘的结构是由两部分组成,称为内圈和外环,内圈与外环通过一个锥度面进行配合,并有螺纹施加压紧力。当螺纹顺时针转动时,内圈和外环的通过锥面接触产生挤压,使得内圈的内径缩小。此时要实现盘与轴产生松动,只需把螺纹逆时针转动,使内圈的内径变大,使得其与轴产生一定的间隙,这样便可产生松动。松动间隙使用游标卡尺控制尺寸大小。 图12 转盘松动结构图 为验证不同油膜间隙对盘轴松动故障的影响,本实验通过替换不同内径的滑动轴承来实现不同的油膜间隙。 如图13、14、15为不同油膜间隙时轴承端的频谱图和运动轨迹实验结果图,可以看到频谱图中主要由转盘转动频率及转轴转动频率组成,随着油膜间隙的增大,运动轨迹经历类似周期运动、混乱运动、类似周期运动状态,且形状越来越细长,与仿真结果吻合。实验结果中转盘转动频率较高,这是由于实验采用的转盘质量相对较大,其幅值必然大。 (a) 频谱图 如图16为转轴中心处的频谱图和轨迹图,可以看到频谱图中含转盘转动频率、转轴转动频率及高倍频,运动轨迹图中也呈扇形。仿真结果与实验结果规律一致,说明仿真结论具有较好的参考价值。 (a) 频谱图 (a) 频谱图 (a) 频谱图 当盘轴松动时,盘轴碰摩和油膜涡动相互影响,必然会造成转子系统响应的复杂性,因此本文基于非稳态油膜力建立了盘轴松动转子-轴承系统的运动方程,用四阶龙格-库塔方法对其进行数值仿真,并采用实验验证。对比分析了考虑油膜力和不考虑油膜力两种支撑情况下转盘的运动状态,并研究了油膜间隙大小对轴承处和转轴中心处运动轨迹和振动特性的影响。结果表明: (1) 对比不考虑油膜力和考虑油膜力这两种情况,研究表明,不考虑油膜力的转子系统转盘无量纲转速在Ω=0.8时,即可进入高转速状态;考虑油膜力的转子系统无量纲转速在Ω=1.3时,才会进入高转速状态。不考虑油膜力的转子系统转盘进入高转速状态时的转轴转速低于考虑油膜力的转子系统。 (2) 轴承端的运动轨迹分别在0 (3) 轴承端的振动频率有转盘转动频率、转轴转动频率,当运动轨迹处于混乱状态时,会出现较微弱的其它倍频成分。转轴中心处的振动频率主要由转盘转动频率、转轴转动频率和特别高的盘轴碰撞频率,有时还会出现微弱的低倍频。轴承端和转轴中心处都无明显的油膜涡动频率出现。转盘转动频率谐波幅值在轴承处和转轴中心处的变化基本一致,当油膜间隙较小时,幅值先急速上升,后急速下降,当油膜间隙较大时逐渐处于平稳状态。转轴转动频率谐波幅值在轴承处和转轴中心处的变化相反,当油膜间隙较小时,轴承处幅值急速上升,而转轴中心处幅值急速下降,当油膜间隙较大时都逐渐处于平稳状态。高倍频谐波幅值在1.6~2.5间来回波动。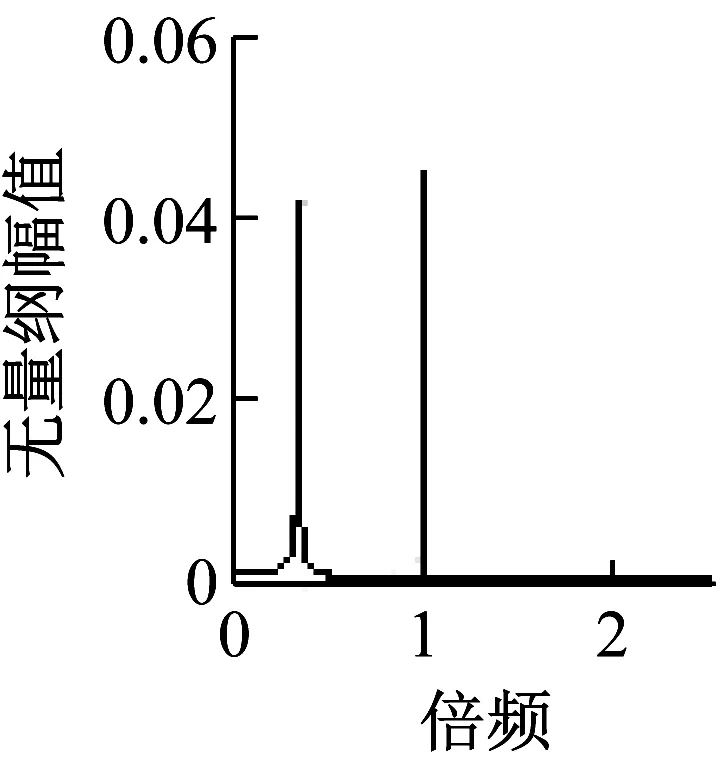



3 实验研究
3.1 实验仪器简介





3.2 实验结果分析


4 结 论

