运输类飞机风挡鸟撞位置影响分析研究

刘信超， 徐亚芳， 王露晨， 陆晓华， 左洪福

(1. 南京航空航天大学 民航学院，南京 211100； 2. 中国民航上海航空器适航审定中心，上海 200335)

作为迎风部件，风挡与尾翼、机翼、缝翼、发动机唇口和吊挂等飞机部位一样，容易遭受飞鸟撞击。据统计，全世界每年大约发生1万次鸟撞飞机事件，国际航空联合会已把鸟害升级为“A”类航空灾难[1]。根据CCAR 25.775条规定，位于正常执行职责的驾驶员正前方的风挡玻璃及其支承结构，必须能经受住1.8 kg(4磅)的飞鸟撞击而不被击穿，此时飞机的速度(沿飞机航迹相对于飞鸟)等于按第25.335(a)条选定的海平面VC值。因此，运输类飞机风挡必须经过地面试验或仿真验证，从而达到抗鸟撞损伤的设计要求。

根据适航审定经验，鸟撞适航审定以试验验证为主。但由于地面鸟撞试验的高昂费用，试验次数十分有限。因此有必要在适航验证之前，通过仿真研究手段对风挡材料、风挡厚度、自由螺栓边和夹紧边缘的不同安装方式、撞击姿态、撞击位置以及撞击速度等参数进行参数化研究，从而对试验进行指导。Doubrava等[2]研究了总厚度为14、18、20 mm的多层风挡在1.8 kg鸟体以83-125m/s速度撞击时的动态响应，发现风挡的临界穿透速度与风挡厚度成正比。Kangas等[3]对不同构型以及不同材料的风挡进行了研究，发现对多层风挡影响最大的因素是聚合物层的厚度。Dar等[4]对PMMA材质的风挡进行了鸟体重量、鸟体形状、速度、撞击角度、撞击位置的参数化研究。Wang等[5]对PMMA材质的风挡进行了环境温度、撞击位置以及撞击速度的影响研究。Mohagheghian等[6]对SGP、PVB、PU层合风挡进行了构型、温度以及厚度等参数的分析研究。

以上的参数化研究均针对有机玻璃风挡，有关无机玻璃风挡的参数化研究较少，而运输类飞机的风挡通常为无机玻璃，因此需要加强对无机玻璃风挡的研究。Grimaldi等[7]对无机玻璃风挡对于撞击角度、撞击目标尺寸以及撞击目标尺寸的敏感性进行了参数化研究，但撞击目标比较简化并忽略了风挡边界的影响。为了充分考察风挡结构的抗鸟撞能力，本文使用真实机头模型以及无机玻璃风挡模型，对撞击位置进行参数化研究，旨在为适航验证试验中的撞击点选取工作提供参考。并从损伤、接触力、位移、应力以及能量变化等方面来综合比较不同撞击点的动态响应，确定不同撞击点的严酷性，并最终为适航工作提供了撞击参考点。

1 鸟体计算模型

1.1 鸟体建模

本文所建的鸟体几何模型为两端带半球帽的圆柱体，纵向总长度为截面直径D的两倍，如图1、2所示。具体建模过程为：首先在CATIA中建立两端带半球帽的圆柱体的几何体，随后导入HyperMesh环境中用Hexa单元离散化鸟体得到图1，最终将图1鸟体导入PAM-CARSH中利用Convert功能转化为SPH模型，如图2。图1、2中的鸟体模型重1.8 kg，尺寸D为0.114 m。

图1 鸟体Hexa单元网格模型

图2 SPH鸟体计算模型

1.2 SPH算法及参数

由于鸟体在高速运动下展现出良好的流体性，故鸟体计算模型一般采用较为成熟的光滑粒子动力学(Smoothed Particle Hydrodynamics，SPH)方法进行建模。SPH算法最初是用在天体物理学领域，是一种插值方法[8]。Liu等[9]以及Monaghan[10]对SPH方法进行了详细的总结。在SPH算法中，计算鸟体被离散成有限个粒子(即插值点)，各粒子均携带速度、密度及应力等物理特性，并根据控制方程的定义随着其他粒子一起运动。每个粒子的物理特性均可以通过对相邻粒子的物理特性进行插值计算得到，可以用规则的内插函数计算全部粒子的场函数值，从而近似描述整个问题的场分布[11]。对于流体动力学问题，相关的控制方程包括连续性方程(即质量守恒方程)与动量方程(即(Navier-Stokes方程)[12]，两个方程的Lagrangian形式见式(1)、(2)。

连续性方程

(1)

动量方程

(2)

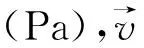
Tait状态方程

(3)

忽略大气压力并将其变成Tait方程中的压强常量p0，因此Tait方程变成Monaghan状态方程[14]

(4)

式中：p为现时压强；ρ/ρ0为鸟体当前密度与初始密度比值；b为体积弹性模量；γ为指数，文献[15]中通过平板试验拟合了b、γ，分别为2.8 GPa、7.99。初始密度ρ0为950 kg/m3。Tait方程的使用对象是弱可压流体，因此b、γ的取值必须保证密度相对变化值|Δρ|/ρ0较小，一般要满足|Δρ|/ρ0≤0.01。同时可知流体速度vf、流体中的声速cs满足式(5)

(5)

因此|vf|/cs需满足|vf|/cs≤0.1，另外，已知体积弹性模量b、指数γ、流体中的声速cs以及初始密度ρ0满足式(6)关系

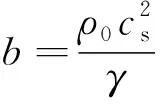
(6)

且本文中的最大流体速度为150 m/s，最终将上述取值代入式(5)、(6)，得到|vf|/cs≈0.087<0.1，说明文献[15]中通过平板试验反演所得鸟体参数的取值满足Monaghan状态方程的使用条件。

1.3 SPH算法验证

本小节给出了依据上述算法所建立的SPH鸟体撞击刚体的数值计算动态响应结果，通过与Wilbeck的试验结果[16]、Zhang等[17]以及Hedayati等[18]的仿真结果进行对比，证明本文SPH算法及其参数的合理性。Zhang等以及Hedayati等的仿真工况条件与Wilbeck的试验条件一致，在Wilbeck的试验中，鸟体重量为1 kg，撞击速度为116 m/s。两端带半球帽的圆柱体1 kg重鸟体仿真模型的尺寸D为0.093 m。因此本小节仿真对鸟体进行了重新建模，鸟体尺寸D变为0.093 m，密度保持不变为950 kg/m3，重量变为1 kg，SPH粒子数为39 456。经过计算，1 kg重的SPH鸟体撞击刚体过程见图3，撞击过程维持约2 ms，本节鸟体动态变形过程与Zhang等的结果基本一致。图4为冲击压强时间历程曲线的对比情况，冲击压强曲线共分为冲击峰及稳流区两个区域。本文SPH算法对冲击压强的冲击峰预测较准，冲击峰的上升趋势及峰值与Wilbeck的试验结果基本一致；虽然较试验结果而言稳流区过于平滑，但稳流区的总体趋势的预测较准，见图4。综上所述，本文的SPH算法及参数是比较合理的。

2 机头计算模型

2.1 机头建模

综合考虑机头结构件的尺寸比、计算精度以及计算效率，用壳单元离散化机头金属钣金件，用实体单元离散化风挡各层结构。在CATIA环境中提取几何模型的外形特征，在HyperMesh环境中修理模型细节，并将模型导入PAM-CRASH后进行计算模型前处理。所有壳单元均为4节点缩减积分单元，壳单元厚度方向设置5个积分点，单个单元边长约14 mm，总单元数为357 599。所有实体单元均为八节点缩减积分单元，单个单元边长约7 mm，总单元数为310 100。所有铆钉用Plink单元模拟，总单元数为8 226。机头结构计算模型及尺寸如图5所示，风挡计算模型如图6所示，风挡各层由外至内为：3 mm厚无机玻璃层、4 mm厚PU胶层、8 mm厚无机玻璃层、1.5 mm厚PVB胶层、6 mm厚无机玻璃层，其中每层无机玻璃的上下表面均有0.5 mm厚的钢化处理层。模型的边界条件为图5(a)中机头侧壁板的所有缘条结构受固支约束。

(a) t=0 ms(b) t=0.7 ms(c) t=1 ms(d) t=2 ms

图3 刚体撞击验证(1 kg，116 m/s)

Fig.3 Verification by impacting rigid target(1 kg，116 m/s)

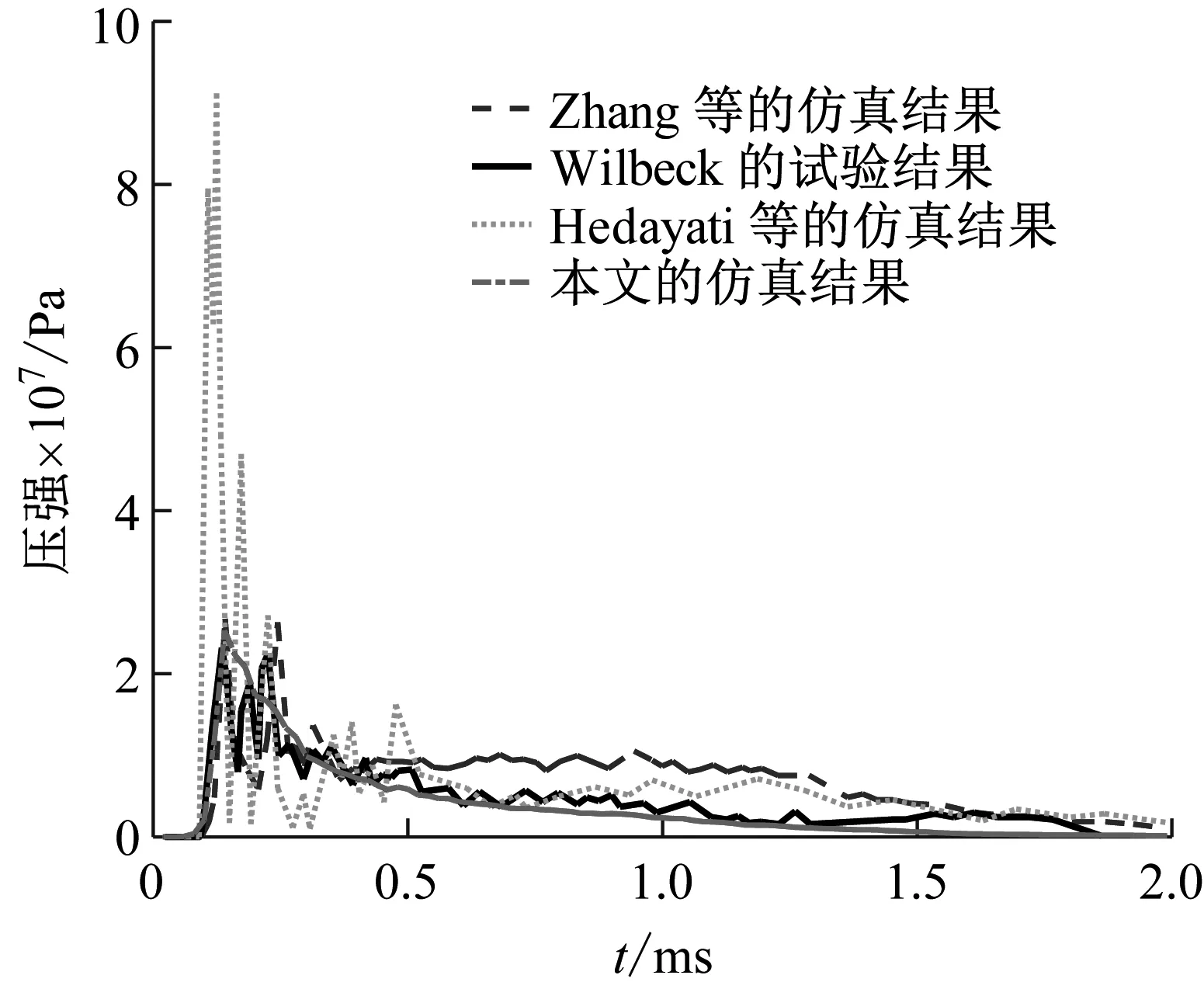
图4 冲击压强时间历程曲线对比

2.2 结构材料及属性

选取PAM-CRASH中102号弹塑性材料模型来描述机头金属结构件的力学行为，其塑性响应用可以反映金属等材料应变硬化效应、应变率强化效应及温度软化效应的Johnson-Cook本构模型描述[19]

(a) 机头整体模型

(b) 连接件模型(Plink单元)

图6 风挡结构计算模型

σe=

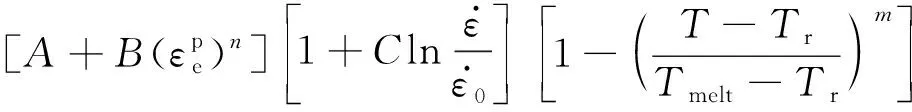
(7)

图5(a)中所示的座舱盖顶部板、侧壁板材料为2524铝合金，风挡下部板材料为2024铝合金，缘条、钣金件的材料为7075、7050铝合金。2024、7075铝合金材料在中应变率至高应变率区间，均表现出较明显的应变率强化效应，在瞬态动力学中须考虑[20]，同时考虑金属材料的应变硬化效应，但忽略温度软化效应。材料的失效行为由等效失效塑性应变εfail进行判定，即当材料的等效塑性应变到达εfail时，认为材料失效，删除其单元。文献[21-24]对上述金属材料的JC本构模型参数进行了测量，具体数值如表1所示。

表1 Johnson-Cook本构模型参数

Plink单元的失效准则为

(8)

式中：N与T分别为拉力和剪切力；Tmax与Smax分别为最大拉力、最大剪切力。本文中所有Plink单元的最大拉力、最大剪切力设为5.1 kN、3.2 kN，指数常量m、n分别设为1.5和2.1。

文献[25]中对航空无机玻璃力学性能进行了试验研究，如图7所示，玻璃材料为典型的脆性材料；应力-应变曲线由弹性加载段和失效段组成，近似为一条曲线；随着应力水平的提高，试样断裂，应力水平急剧下降。因此本文选取PAM-CRASH中16号弹塑性本构来描述其力学性能，其中失效删除塑性应变取0.001。由图7可知，无机玻璃的强度对应变率较为敏感，400 s-1应变率下的强度(1.1 GPa)几乎为准静态时强度(0.517 GPa)的两倍。同时，本文考虑了无机玻璃表面化学钢化处理的影响。文献[26]中表明，视窗玻璃经过化学钢化后，表面离子交换层的准静态强度可达到0.8 GPa。由于缺乏表面离子交换层的高应变率下力学性能数据，本文较为保守地采用准静态下的玻璃强度，其中中间未钢化层强度取0.517 GPa，表面钢化层强度取0.8 GPa。文献[27-28]中给出了PU胶层以及PVB胶层的动态应力-应变曲线，如图8所示，本文同样采用选取PAM-CRASH中16号弹塑性材料模型近似地描述其力学行为。

3 撞击位置选取

图9为本仿真中选取的各个撞击点，其中A1～A11位于风挡表面，B1～B3位于风挡中央加持结构表面。A1～A11全部位于航向右风挡，由于飞机机身具有对称性，因此不对航向左风挡进行重复计算分析。本文选取的A1～A11、B1～B3撞击点所包含的撞击区域基本覆盖了航向右风挡全部表面区域及中央夹持部件区域，其中A10、A11位于风挡边角点，A5位于风挡中心点。本文对上述撞击点依次进行鸟撞仿真计算，计算结果作为后续分析的输入。上述所有撞击工况中，鸟体撞击方向均沿着机身方向，鸟体姿态无偏航无俯仰，撞击速度均为150 m/s。

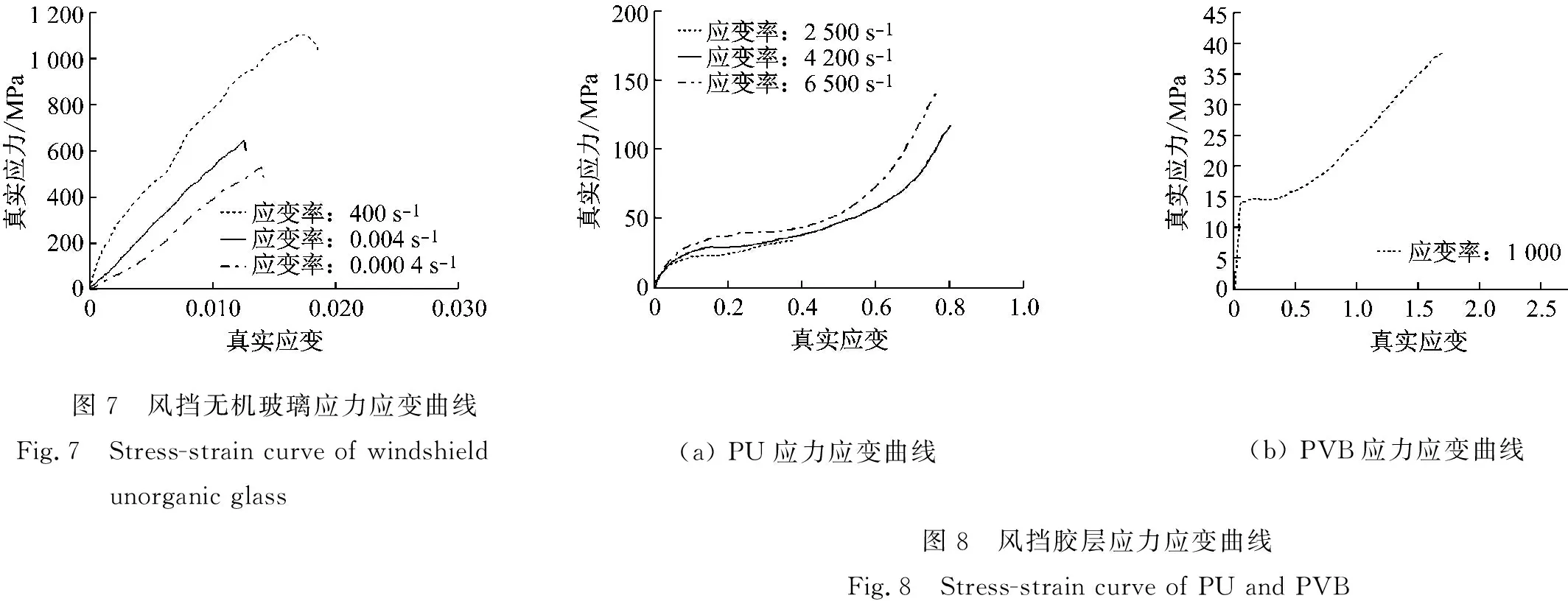
图7 风挡无机玻璃应力应变曲线 Fig.7 Stress-strain curve of windshield unorganic glass(a) PU应力应变曲线(b) PVB应力应变曲线图8 风挡胶层应力应变曲线Fig.8 Stress-strain curve of PU and PVB

图9 撞击点位置示意图

4 仿真结果分析

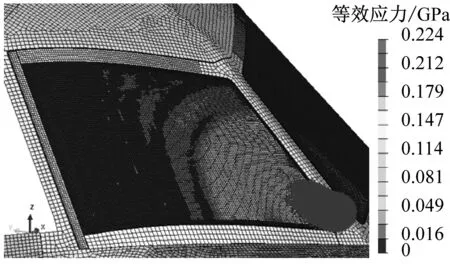
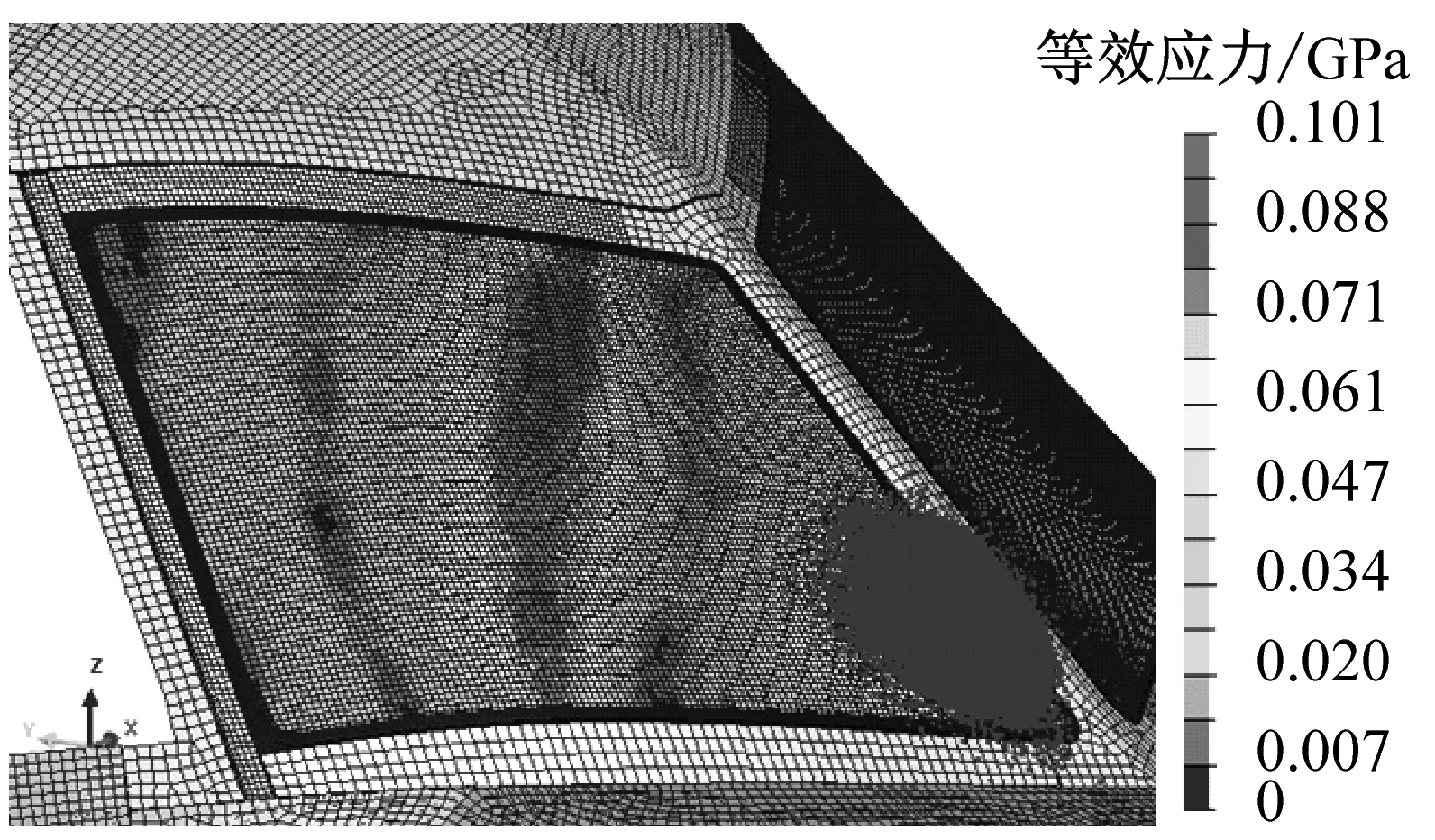
从损伤结果对比各工况，发现仿真中仅在A10点对应工况下出现风挡的稍许单元删除，且单元删除仅存在于最外层无机玻璃的表面层，其它层均无损伤。本节以A10对应工况为例分析鸟撞模拟过程：鸟体以150 m/s的速度飞向预定着弹点，鸟体在接触风挡玻璃的瞬间产生高冲击压力，撞击点处的个别风挡单元产生应力集中现象并发生删除，如0.16 ms时，接触部位某单元的范式等效应力达到759 MPa，而后该单元删除。同时撞击点处出现凹陷，随着时间的推移，凹陷区域经历了加深、转移、回弹现象，当接触时间达到3 ms后，鸟体作用力所剩无几并随后沿风挡表面逐渐滑出，图10给出了t=0 ms到t=3 ms过程中风挡与鸟体的耦合作用过程以及层合风挡的受力情况。

(a) t=0.4 ms

(b) t=0.8 ms

(c) t=1.6 ms

(d) t=3.0 ms

图10 鸟撞过程及风挡Von Mises等效应力云图(150 m/s)

Fig.10 Bird-strike process and Von Mises stress contour(150 m/s)

除了损伤情况，本文也从接触力、动能损失程度、风挡结构变形、窗框结构受力等多个角度来比较工况严酷程度。图11为接触力时间历程曲线，图12为鸟体动能损失曲线。由图11、图12可知，各撞击点对应的接触力及动能变化趋势基本一致，但接触力峰值与剩余动能的大小显著不同。以4 ms时刻的鸟体动能为剩余动能，并提取了各撞击点对应的剩余动能及接触力峰值，得到了图13。

图11 接触力时间历程曲线

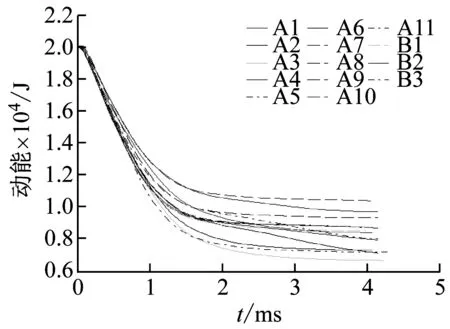
图12 鸟体动能损失曲线

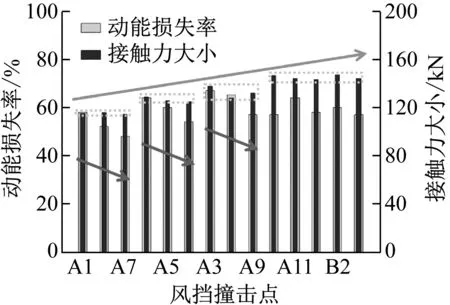
图13 不同撞击位置时的动能损失与接触力对比

Fig.13 Comparison between different impact positions about kinetic energy loss and contact force

根据仿真结果可知，如图13箭头所示，鸟体越靠近飞机机身纵轴，接触力峰值越大；鸟体越靠近飞机机身纵轴，鸟体动能损失更大。A3、A6、A9、A10、A11、B1、B2、B3各工况下，鸟体均在纵轴附近，因此接触力均表现为较大值。其次，根据对比分析发现，撞击点的竖直位置对接触力与鸟体动能损失的影响不明显，如B1、B2、B3各工况下接触力与动能损伤的对比情况。

图14为鸟体动能变化与风挡变形情况对应关系，其中风挡变形情况由风挡上某一特殊点的位移来表征。该点取为对应工况下接触力峰值出现时风挡背面上位移量最大点，本文以该点代表对应工况下风挡的变形情况。由图14可知，当撞击点距离风挡上下夹持边界较远时，即A3、A4、A5三个撞击点，风挡的变形量较大，而其他工况下由于风挡受到边界夹持部件的影响，风挡变形情况偏小。层合风挡通过变形耗散部分鸟体动能，中心撞击点A5撞击工况下层合风挡吸收能量最多并达到342.7 J，边角撞击点A7撞击工况下层合风挡吸能最少且仅有255.08 J，表明当着弹点位于窗框边界附近时，窗框会通过自身支持刚度减少风挡变形吸能。然而窗框结构的支持刚度对各撞击点的影响不同，如位于下边角的A10工况下层合风挡吸能为263.80 J，而位于风挡上边角的A11工况在接触力与A10相当且均位于边角的情况下，风挡吸能较大且为302 J，说明上下侧窗框的支持刚度存在差异，会影响风挡的吸能过程。

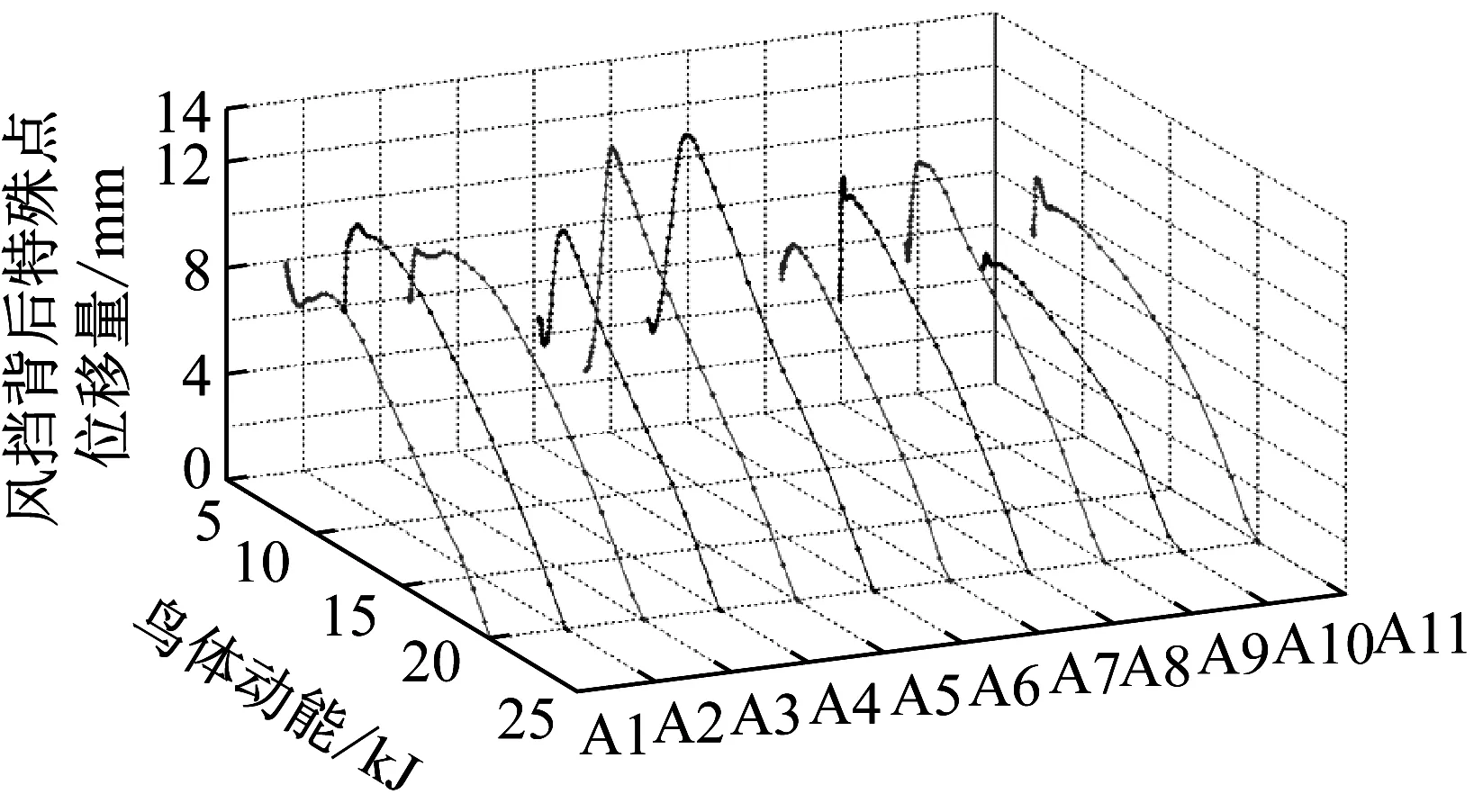
图14 鸟体动能变化与风挡变形情况对应关系

除了风挡内能外，窗框结构支持刚度对能量分配的影响也体现在自身内能变化过程中，窗框结构也通过变形行为耗散部分鸟体动能。考虑到各部位支持刚度的不同，图15中将窗框结构分为上侧、下侧、外侧以及中央窗框四个部位，图16中对上述窗框各个部位出现的内能峰值进行了统计。由于A1、A4、A7各工况的接触力较小(见图13)，且处于风挡外侧的位置，鸟体易滑走，威胁较小，因而图16中未包含该三点。此外，由于窗框各部位与着弹点的距离不同而导致应力波到达各部位的时间不同，故每一个撞击工况下都分别单独考虑四个部位的内能峰值大小，即忽略各部件的峰值到达时间。

图15 窗框结构

图16中的圆圈表示对应结构出现了较大的内能以及较大的变形，其中A系列撞击点中，A2对上侧窗框影响最大，A9对下侧窗框影响最大，A11对中央窗框影响最大；在B系列撞击点中，B2对中央撞击点影响最大；所有撞击点对外侧窗框的影响均明显小于对其他窗框结构的影响，因此忽略对外侧窗框的分析。经过应力分析发现，这些对应结构出现应力集中现象：在A2撞击工况中，上侧窗框Von Mises应力在1.12 ms时达到544 MPa；在A9撞击工况下，下侧窗框Von Mises应力在1.6 ms时达到517 MPa；在A11撞击工况下，中央窗框Von Mises应力在2.08 ms时达到329 MPa；在B2撞击工况下，中央窗框Von Mises应力在2.32 ms时达到349 MPa。以A2工况为例，给出上侧窗框结构的Von Mises等效应力云图，如图17所示，其集中应力已经超过材料的屈服强度473 MPa，局部产生塑性变形。

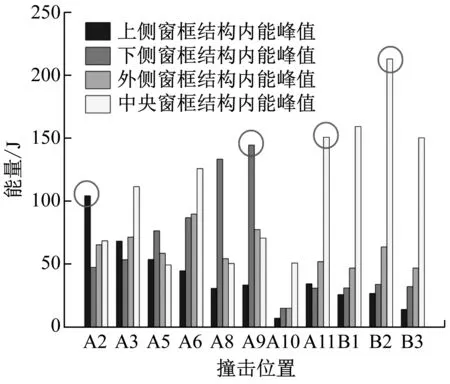
图16 窗框结构内能峰值分布

图17 A2工况下上侧窗框结构Von Mises等效应力云图(背面)

综上所述，为了充分验证风挡的抗鸟撞安全性，必须考虑到鸟体距离机身纵轴远近、边界夹持部件两大因素的影响。因此建议在验证试验中选取A2、A9、A11、B2四点作为试验靶点。

5 结 论

本文以飞机无机玻璃层合风挡为研究对象，研究了无机玻璃层合风挡的鸟撞动态响应特点及撞击后果严重性与撞击点分布位置的关系。在150 m/s撞击速度下，该飞机风挡各工况的计算损伤结果均表现出了对适航条款的符合性，然而在接触力、风挡变形以及能量变化情况上显示出了明显的差异。本文通过参数化研究来了解这些差异性，并以此为参考挑选出具有代表性的撞击点作为试验靶点，可以为审定试验提供参考，避免大量试验所带来的高成本。本文的参数化研究得到了以下结论：

(1) 越靠近飞机机身纵轴，鸟体与风挡之间的接触力越大，飞机吸收的鸟体动能越大。

(2) 对于不同冲击点而言，风挡的变形情况明显受到边界夹持部件的影响，不可忽视。

(3) 窗框结构不同部位的支持刚度存在差异，会影响风挡及窗框结构的吸能过程，且当着弹点靠近夹持边界时，对应夹持部件出现应力集中现象。

(4) A2、A9、A11、B2四点适合作为适航验证试验靶点。