海洋高桩基础水平振动特性分析

付 鹏， 胡安峰， 李怡君， 谢康和， 李 龙

(1. 浙江大学 滨海和城市岩土工程研究中心，杭州 310058；2. 浙江大学 软弱土与环境土工教育部重点实验室，杭州 310058)

随着港口及海洋工程的发展，桩基础作为一种有效的基础形式在跨海大桥、码头、近海风机、海上平台建设中得到了广泛的应用。在风荷载、波浪荷载、地震荷载等荷载作用下，海洋桩基需要承受巨大的水平动荷载。研究其在动力荷载作用下的水平振动特性具有重要的工程应用价值。

近几十年来广大学者对动荷载作用下桩基振动问题进行了深入的研究。Novak等[1-4]将土体视为均质黏弹性介质，系统的研究了动力荷载作用下桩基水平振动问题。Gazetas等[5]基于分象限假定研究了桩-土系统水平振动的辐射阻尼。Shadlou等[6]基于弹性动力学理论，分析了成层地基中单桩水平动力响应。尚守平等[7]，Zheng等[8]将土体视为饱和多孔介质，研究了饱和土中桩基水平振动问题。

这些研究均是基于完全埋入式桩基础，然而海洋桩基多采用高桩的形式，上部桩体位于水中，下部桩体埋入海床，其变形和内力与完全埋入式桩基有明显的差异[9-11]。马宏旺等[12]采用数值模拟的方法研究了循环荷载作用下高桩基础水平动力特性。Catal[13-14]将土体视为弹性连续介质，研究了高桩基础的动力稳定特性。任青等[15]基于动力Winkler模型，提出了考虑竖向荷载的海洋群桩基础水平振动模型。Hu等[16]基于饱和多孔介质理论，分析了饱和土地基中高桩基础的水平动力响应，探讨了埋入比对桩基振动特性的影响。Liu等[17]基于叠加原理，研究了成层饱和土地基中群桩水平振动特性。

以上研究都是将高桩基础埋入水中部分桩体考虑为自由段，没有考虑作用在桩身上的动水压力。徐汉忠[18]的研究表明动水压力会对埋入水中圆柱梁的水平振动特性产生显著影响。本文假设水体为无黏性不可压缩流体，考虑桩基与海床土及流体的相互作用，基于传递矩阵法，得到了海洋高桩基础水平振动解析解。本文解可为海洋高桩基础的工程设计提供参考。

1 计算模型及基本假定

计算简图如图1所示，水深为H1，土层厚度为H2，桩顶受到简谐激振力，桩体弹性模量为Ep，桩体密度为ρp，桩长为H，半径为r0。

图1 计算模型

本文在建立模型时引入以下假定：①土体为各向同性黏弹性体，水体为无黏性不可压缩流体；②桩-流体、桩-土体系振动为小变形，桩-流体、桩-土完全连续接触；③水平振动时，忽略土体的竖向位移；④桩底为固定支座，桩顶自由。

2 控制方程及边界条件

2.1 振动控制方程

(1)流体运动控制方程

无黏性不可压缩流体的运动控制方程是拉普拉斯方程，在柱坐标系下可表示为

(1)

式中,φ为速度势函数

(2)土体振动方程

根据弹性动力学理论，不考虑土体竖向位移时，柱坐标下土体振动控制方程可表示为

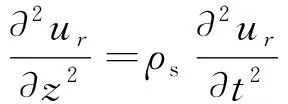
(2)

(3)

式中：ur和uθ为土体径向和切向位移；λ和μ为土体复拉梅常数，μ=G(1+2ξi)，G为土体剪切模量，ξ为土体阻尼比；ρs为土体密度。

土体振动方程相关解可参考文献[2]，这里不再详细说明。

(3)桩水平振动方程

(0≤z≤H2)

(4)

(-H1≤z<0)

(5)

式中：up为桩身水平位移；Ep为桩弹性模量；Ip为桩截面惯性矩；mp为桩单位长度的质量；qs为水平振动时单位长度桩身所受的土体反力；qf为作用于单位长度桩身的动水压力。

2.2 边界条件

(1)不考虑重力波的影响，流体表面有

φz=-H1=0

(6)

(2)流体底面z=0处无竖向速度，有

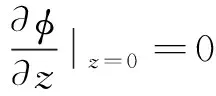
(7)

(3)流体与桩身接触面速度连续，即

(8)

(4)无穷远处，速度势满足Sommerfeld辐射条件

(9)

式中：kw为波数。

土层边界条件及桩土接触面连续条件可参考文献[2]，这里不再详细介绍。

3 方程求解

基于分离变量法，流体速度势函数φ可表示为

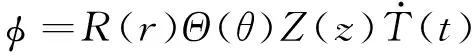
(10)

式中，T(t)为时间因子eiωt，为简便起见，在以下推导过程中省略eiωt项。

将式(10)代入式(1)，可解得

R(r)=A1Im(hr)+A2Km(hr)

(11)

Θ(θ)=B1cos(mθ)+B2sin(mθ)

(12)

Z(z)=C1cos(hz)+C2sin(hz)

(13)

式中，Im(hr)和Km(hr)分别为m阶第一类、第二类修正Bessel函数。

结合边界条件和桩-流体耦合连续条件(6)、(7)、(8)、(9)，可有

A1=B2=C2=0,m=1

(14)

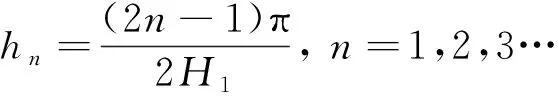
(15)

则速度势函数φ可表示为

(16)

作用在桩身上的动水压力为

(17)

式中，ρf为流体的密度。

将式(16)代入式(17)，可得

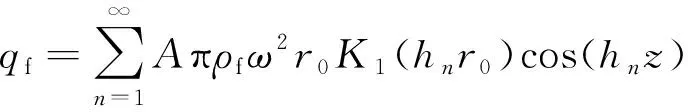
(18)

将式(18)代入式(5)，则埋入水中部分桩身振动方程可表示为

(19)

式(19)的解为

up=λ1cosh(kz)+λ2sinh(kz)+λ3cos(kz)+

(20)

式中：k4=mpω2/EpIp；λ1，λ2，λ3，λ4为待定常数。

由桩-流体接触面速度连续条件，可有

[λ1cosh(kz)+λ2sinh(kz)+λ3cos(kz)+λ4sin(kz)-

(21)

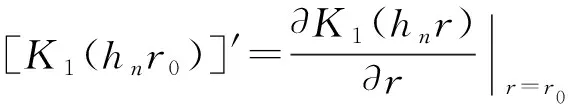
将式(21)两边同时乘于cos(hnz)，并在区间[-H1，0]上积分，可有

(22)

由式(22)可得

A=δ1λ1+δ2λ2+δ3λ3+δ4λ4

(23)

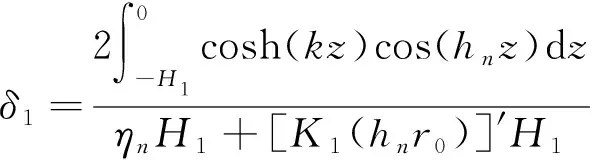
(24)

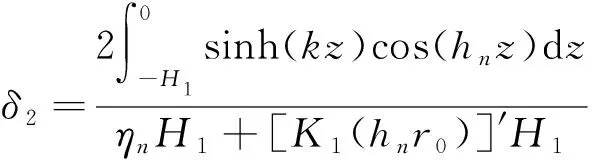
(25)

(26)

(27)

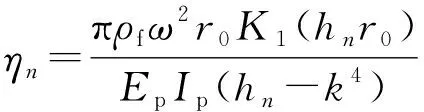
则式(20)可表示为

up=

(28)

故对于埋入水中部分桩身可有

(29)

式中：up,φp，Mp，Qp分别为桩身水平位移、转角、弯矩和剪力；[T1(z)]=[t1(z),t2(z),t3(z),t4(z)]其中

[t1(z)]=

(30)

[t2(z)]=

(31)

[t3(z)]=

(32)

[t4(z)]=

(33)

由此可得桩顶和流体-土交界面处桩身位移及内力的关系

(34)

同理，桩底和流体-土交界面处桩身位移及内力关系为

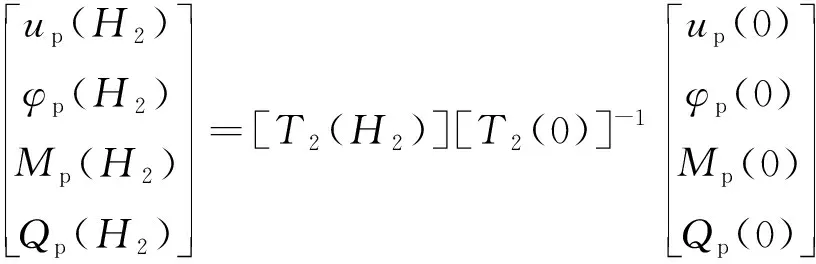
(35)

式中，[T2(z)]和[T1(z)]矩阵形式相同，具体参数取值见文献[3]

水中段及土中段桩身在流体-土交界面处位移和内力连续，则由式(34)和(35)可得

(36)

其中，

[T]=[T2(H2)][T2(0)]-1[T1(0)][T1(-H1)]-1

当桩底为固定约束时，有

up(H2)=0，φp(H2)=0

(37)

由式(36)和(37)可得

(38)

式中，

[Kp]=

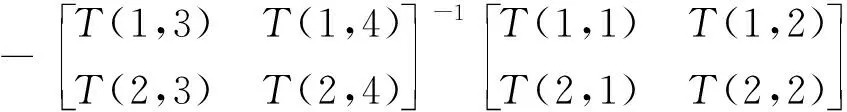
(39)

则桩顶水平动力阻抗Kh，摇摆动力阻抗Kr以及水平-摇摆耦合动力阻抗Khr可分别表示为

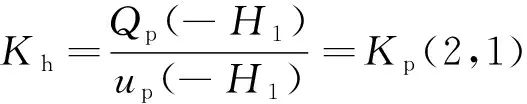
(40)

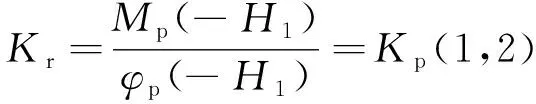
(41)

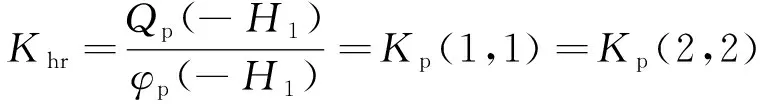
(42)

4 计算结果与分析

4.1 合理性验证

为验证本文解的正确性，将本文解与文献[18]给出的圆柱梁与水耦合振动解对比。令H2=0，将本文解退化为水中圆柱梁水平振动解，计算得到水中圆柱梁的梁顶动力阻抗。计算参数为：H1=5 m，r0=0.5 m，Ep=25 GPa,ρp=2 500 kg/m3，ρf=1 000 kg/m3。对角频率ω进行转化，横坐标为f=ω/2π。图2分别给出了根据本文退化解和文献[18]解得到的水平动力阻抗计算结果。可以看出两者分析结果完全一致，从而验证了本文解的合理性。

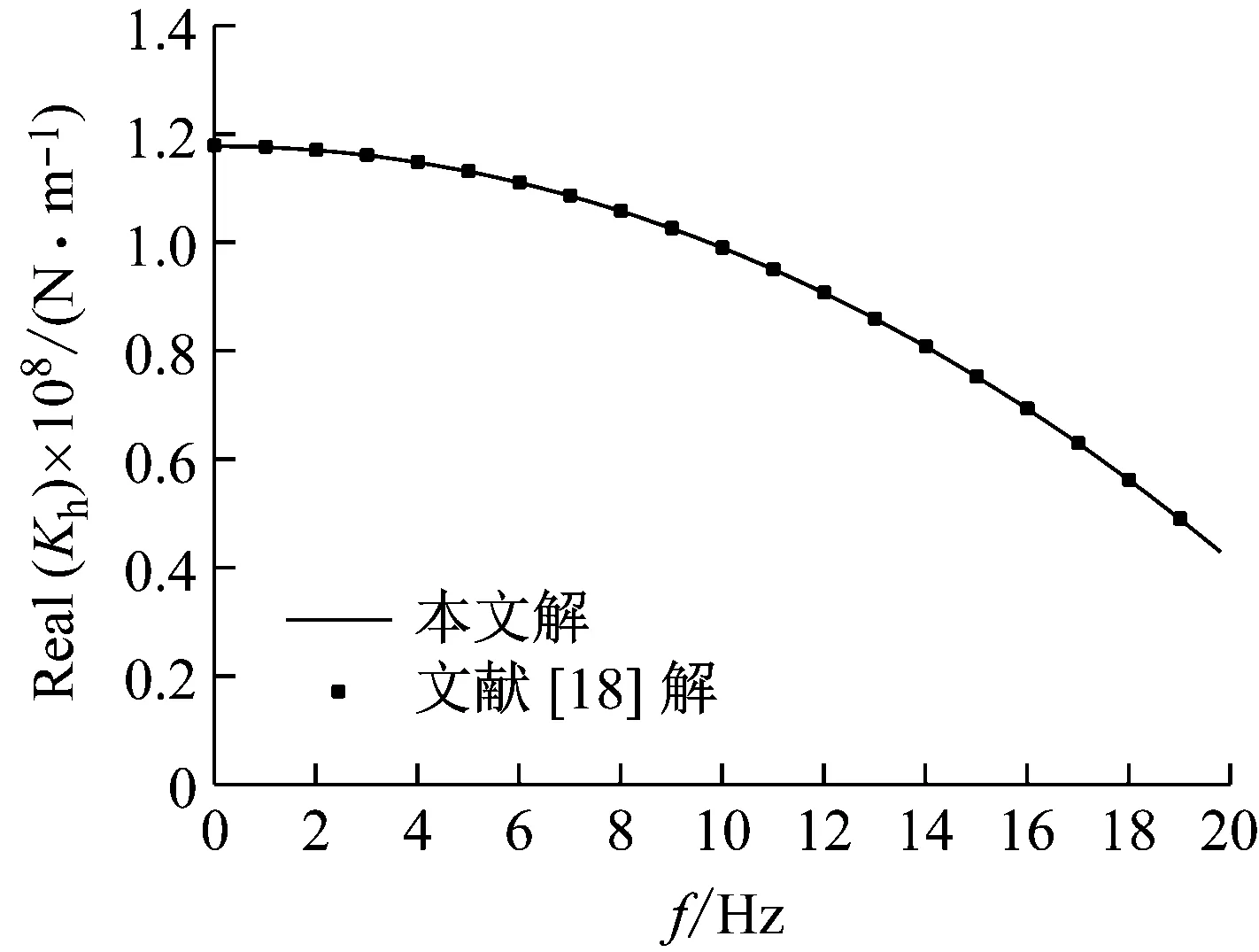
图2 与文献[18]解对比分析

为进一步验证本文解的合理性，令H1=0，将本文解退化为完全埋入式桩基水平振动解，并与文献[3]解进行对比。计算参数为：H2=20 m，Ep/Es=1 000，νs=0.3，ξ=0.05，ρs=2 190 kg/m3，其余参数同上。图3分别给出了根据本文退化解和文献[3]解得到的水平动力阻抗计算结果。可以看出两者分析结果完全一致，进一步验证了本文解的合理性。

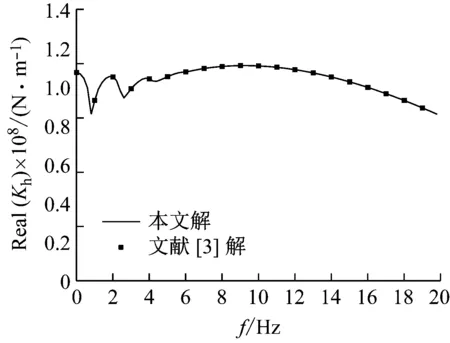
(a)

(b)

4.2 桩顶动力阻抗特性分析

对海洋高桩基础桩顶阻抗特性进行分析，主要分析动水压力、水深及桩径对桩顶阻抗的影响。其中，桩顶阻抗的实部代表真实的刚度，虚部代表桩-土及桩-流体系统能量消散的阻尼。参数分析中，计算参数取值为H2=20 m，H1/H2=0.1，其余参数同上。

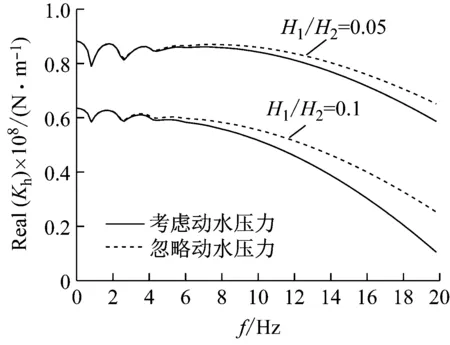
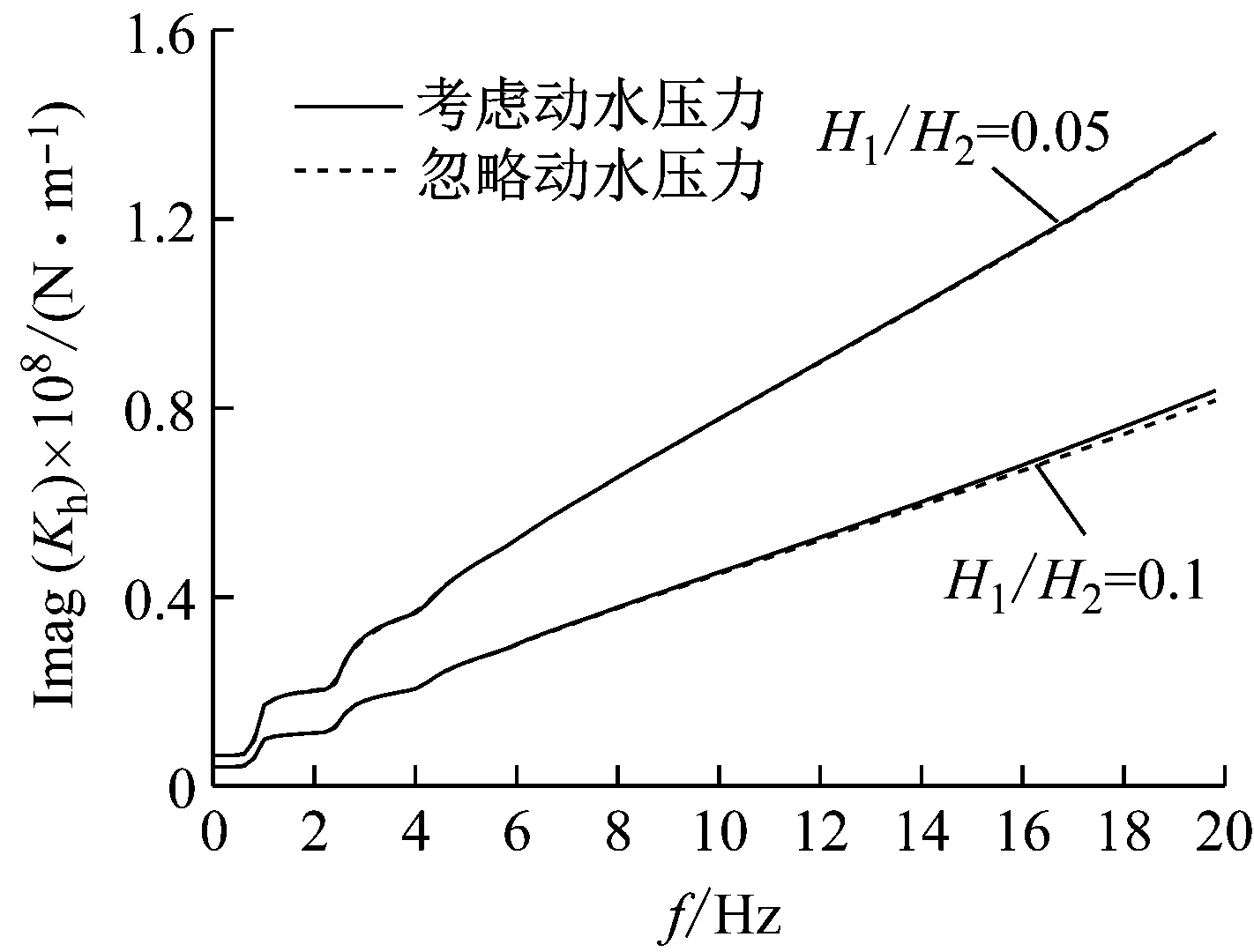
为分析动水压力对海洋高桩基础水平动力特性的影响，将本文解与不考虑动水压力的解进行对比分析。图4和图5分别反映了不同水深及不同桩径下动水压力对桩顶水平动力阻抗的影响。由图可见，频率较低时，动水压力对桩顶水平动力阻抗影响不大。在较高频率范围，考虑动水压力计算得到的水平阻抗刚度因子小于忽略动水压力计算得到的水平阻抗刚度因子，且两者的差距随频率增大而增大。当频率较高且水深较深时，考虑动水压力计算得到的水平阻抗阻尼因子略微大于忽略动水压力计算得到的水平阻抗阻尼因子。结合式(18)可以看出，动水压力随激振频率的增大而增大；ω=0时，动水压力等于0。从而随着激振频率的增加，动水压力对桩顶水平动刚度影响越大。这与图4、5的分析结果一致。说明在进行海洋高桩基础水平动力特性分析时，需要考虑动水压力作用，以免高估其水平动刚度。

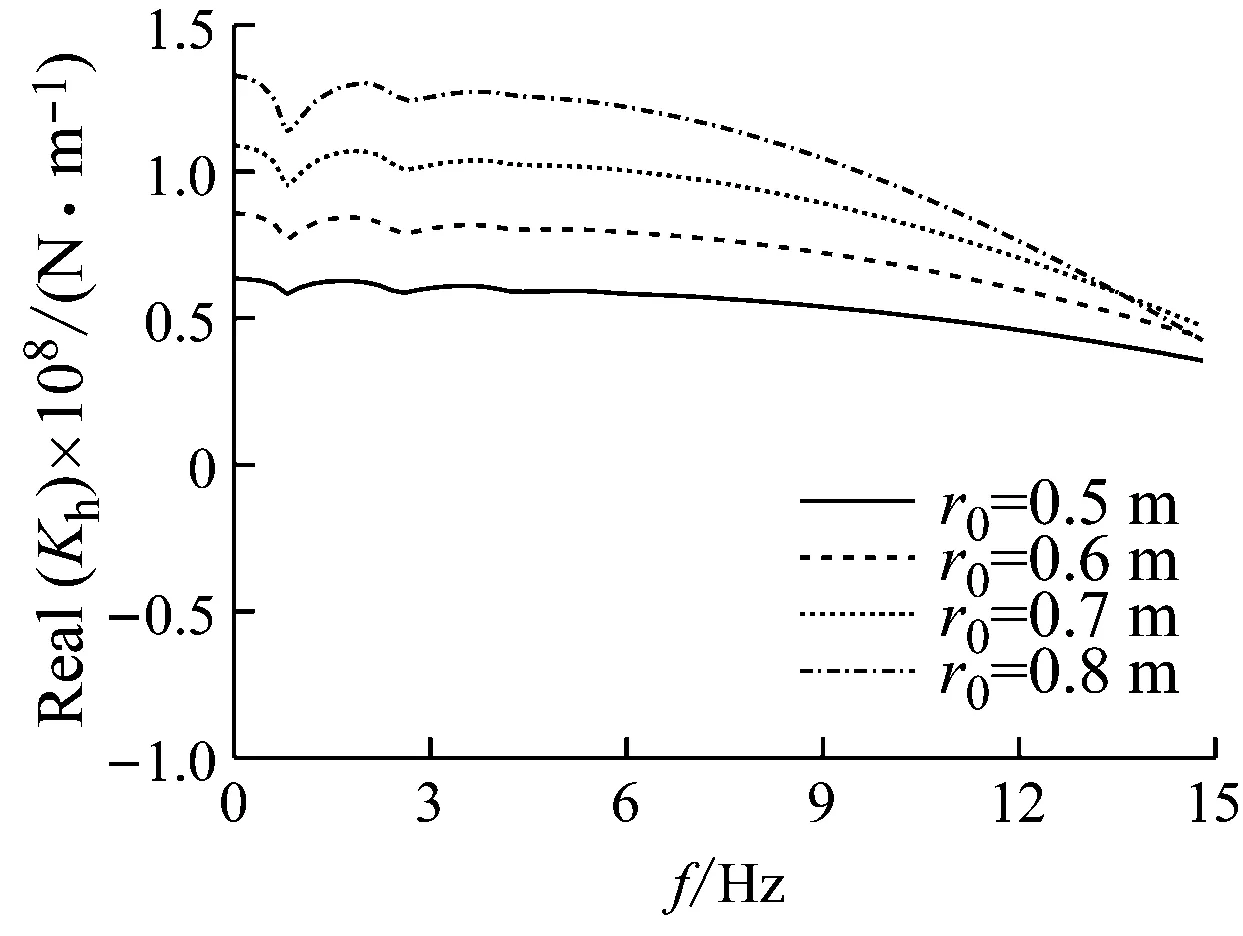
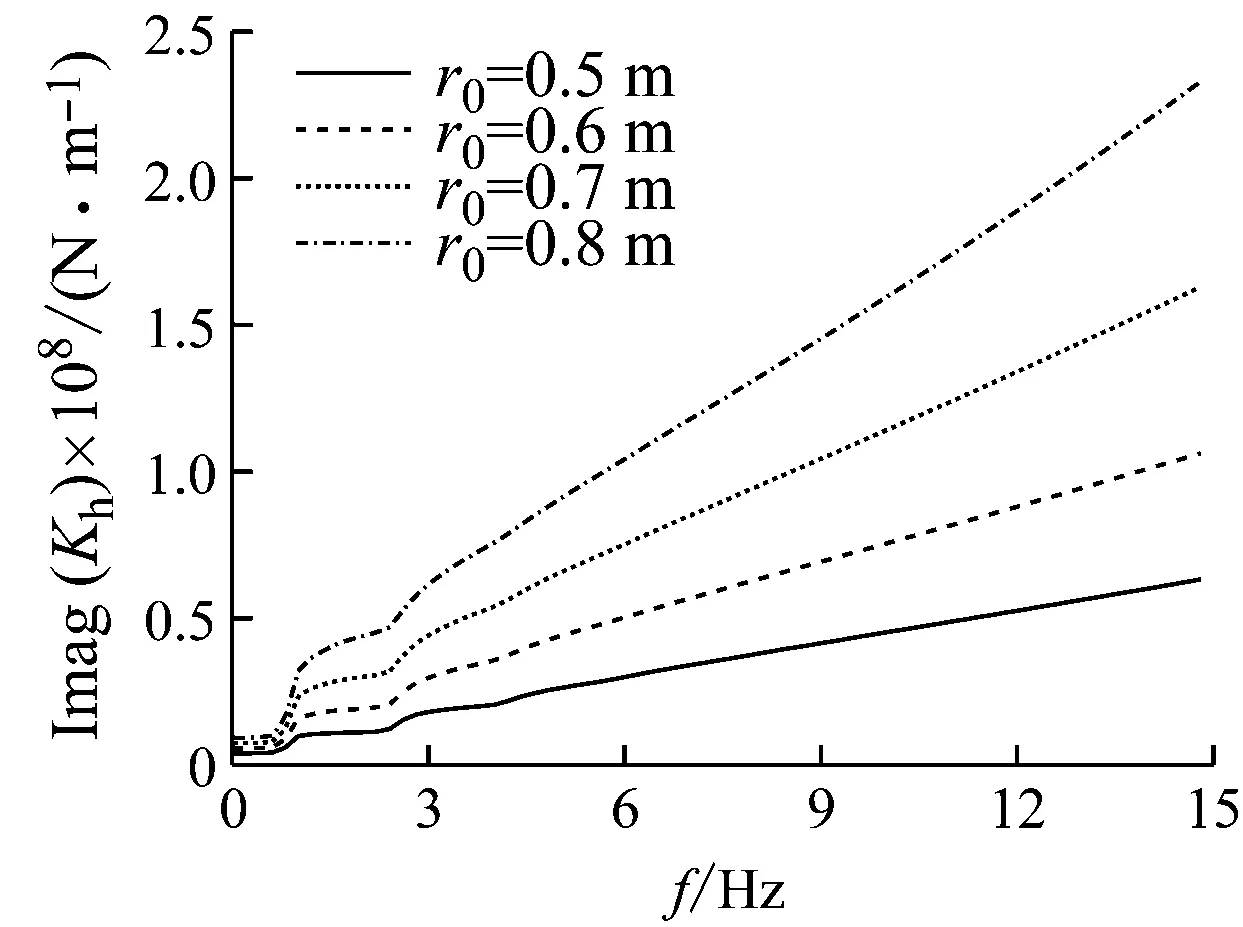
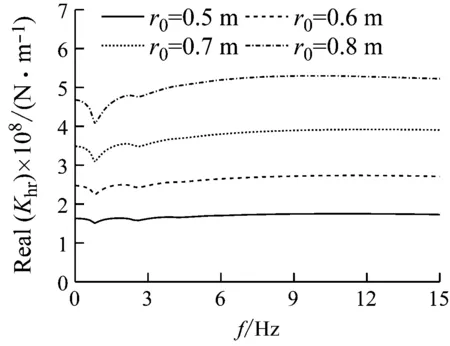
图6～图8反映了桩半径对桩顶阻抗的影响。由图可见，增大桩径对桩顶阻抗提升非常明显。但是随着频率增加，桩径对水平阻抗刚度因子影响逐渐减小。这是由于随着桩径增加，土体反力及桩身刚度增加，单位长度桩身质量也随之增加。在低频范围内，水平阻抗刚度因子主要受桩身刚度及土体反力影响。但是在较高频率范围，桩身惯性力对水平阻抗刚度因子的影响更为显著。

(a)

(b)

(a)

(b)

(a)

(b)

(a)

(b)

(a)

(b)

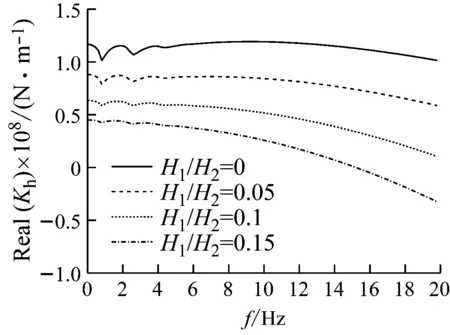
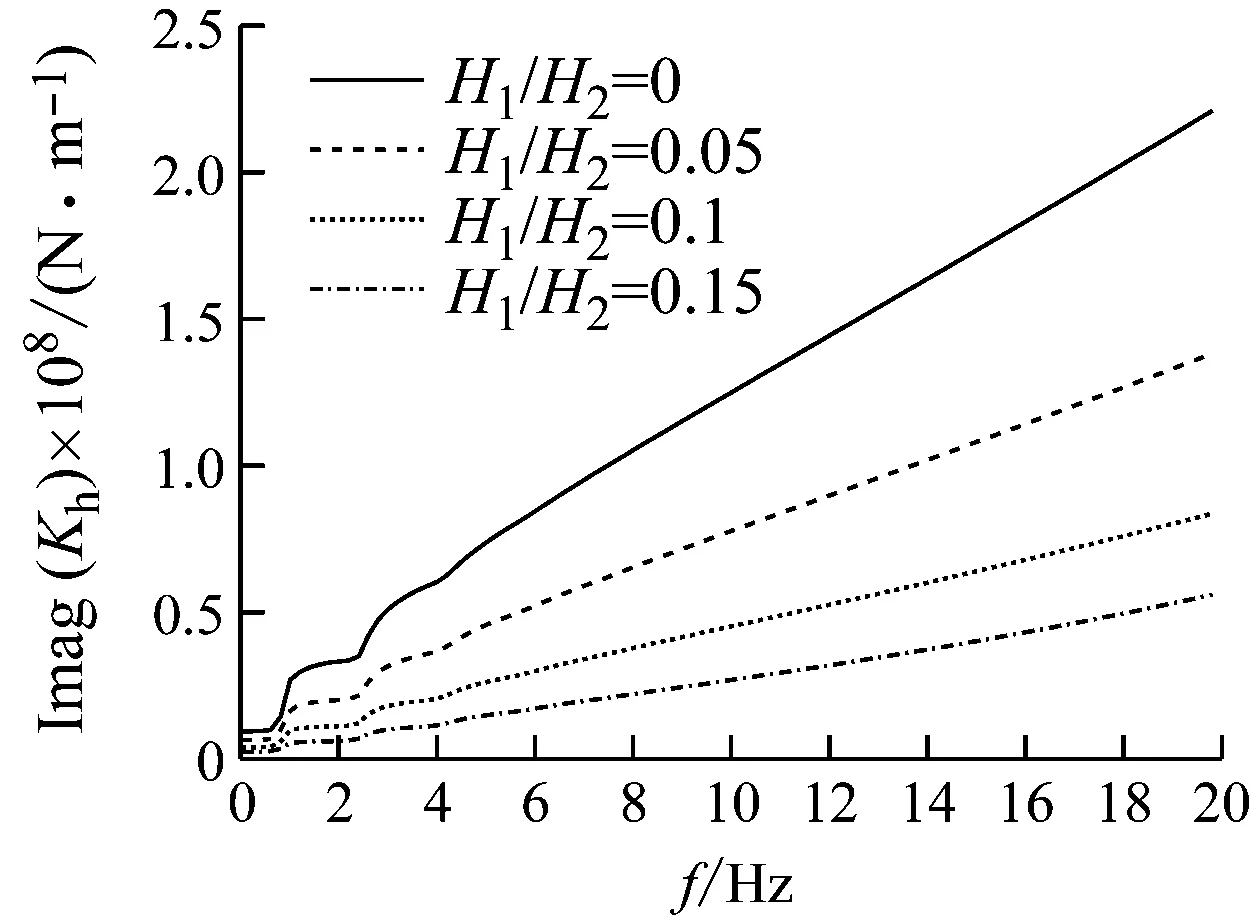
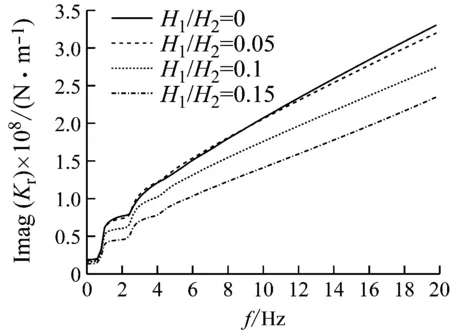
图9～图11反映了水深对桩顶阻抗的影响。可以看出当桩体埋入土中长度和桩径一定时，随着水深增加，水平阻抗、摇摆阻抗、水平-摇摆耦合阻抗均显著减小。且随着频率增加，桩顶阻抗降低幅度明显加大。当H1/H2=0.1时，桩顶水平动刚度相较于完全埋入式桩基础降低了45%以上。说明桩基础的动力特性对上部约束条件非常敏感。

(a)

(b)

(a)

(b)

(a)

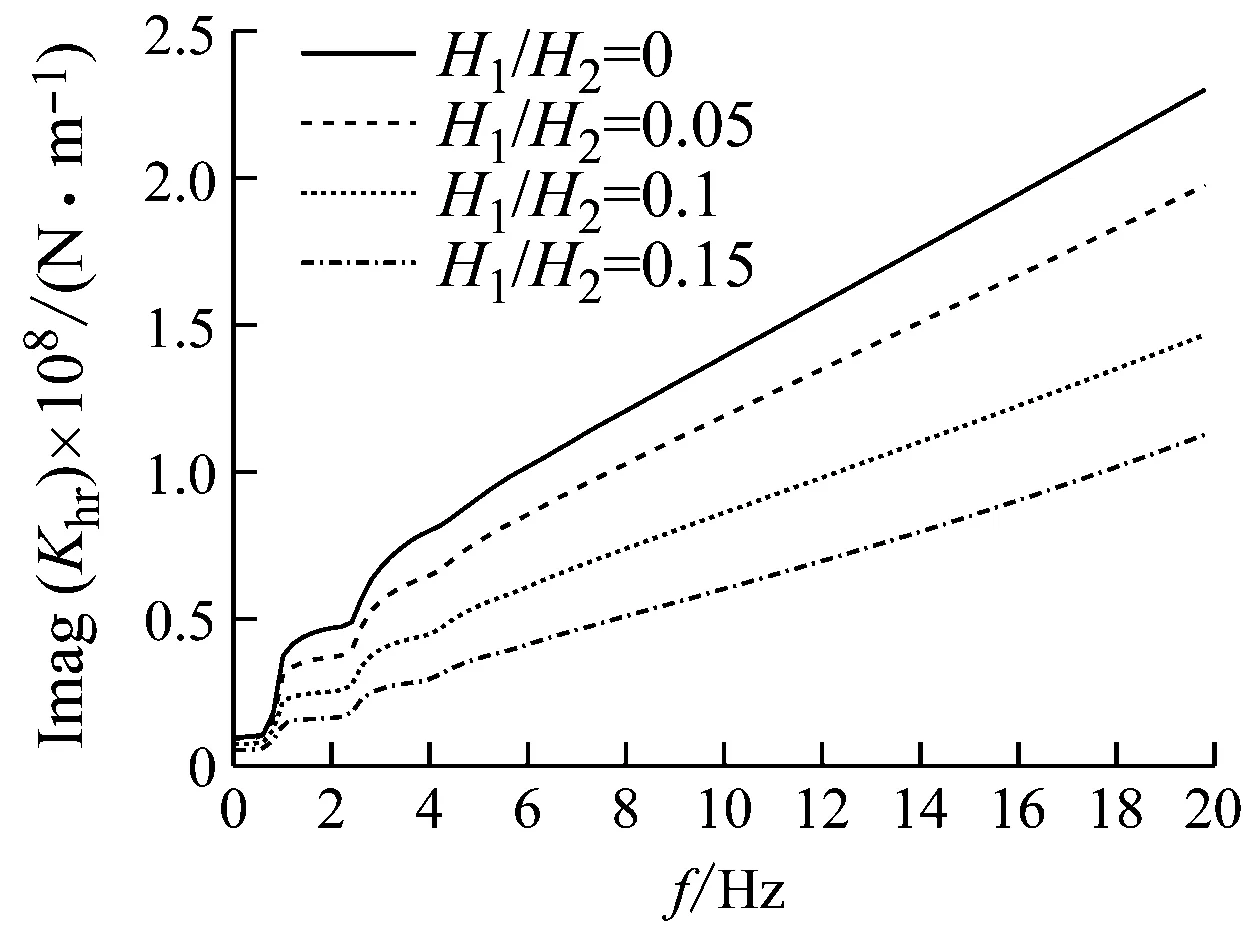
(b)

5 结 论

本文考虑动水压力作用和桩-流体耦合振动，得到了黏弹性地基中海洋高桩基础水平动力响应解析解。对桩顶阻抗进行参数分析，得出了以下结论：

(1)频率较低时，动水压力对桩顶水平动刚度影响不大，在较高频率范围，忽略动水压力会高估桩顶水平动刚度。

(2)频率较低时，动水压力对桩顶水平阻抗阻尼因子影响很小，当频率较高且水深较深时，忽略动水压力会低估桩顶水平阻抗阻尼因子。

(3)增大桩径对桩顶阻抗提升非常明显，但是随着激振频率增加，桩径对水平阻抗刚度因子的影响逐渐减小。

(4)水深的增加会显著降低高桩基础水平阻抗、摇摆阻抗及水平-摇摆耦合阻抗。且随着频率增加，桩顶阻抗降低幅度明显增大。