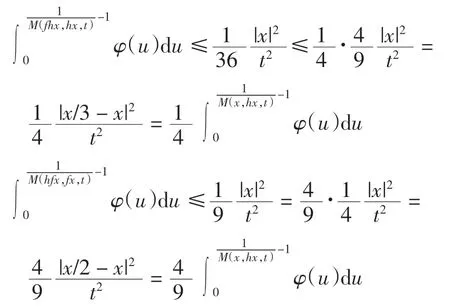模糊度量空间中一类积分型压缩映象公共不动点定理

张树义，张芯语，聂 辉

（渤海大学数理学院，辽宁锦州121013）

1 引言与预备知识

不动点理论广泛应用于多个数学研究领域，如微积分方程解的存在唯一性问题等.研究各种非线性映射在不同空间中的不动点存在性和算法及其应用是非线性泛函分析的研究热点之一.文献[1-5]讨论了模糊度量空间的几种定义.文献[6-7]修正了文献[5]给出的模糊度量空间的概念，并在这类模糊空间中获得了Hausdorff 拓扑.文献 [8-9]证明了依George 和Veeranani 意义由模糊度量空间诱导的拓扑是可度量的.文献[10]依Kramosil 和Michalek 意义，在模糊度量空间中获得了Banach 压缩原理模糊形式.此后文献[11 -13]在 Kramosil 和Michalek 以及 George 和Veeranani 意义下，在模糊度量空间中得到了一些不动点定理，其中文献[11]引入模糊度量M 满足三角不等式的概念，并在模糊度量空间中得到一些不动点定理.文献[14]在模糊度量空间中建立了模糊度量M 满足三角不等式的一类压缩映象的公共不动点定理.文献[15-16]在模糊度量空间中研究了Φ-压缩映象的一些不动点定理.文献[17]证明了模糊度量空间中模糊ψ-压缩序列的不动点定理.文献[18]证明了模糊度量空间中2 种弱相容映射的公共不动点定理.文献[19]证明了概率和模糊度量空间中φ-压缩映射的不动点定理.文献[20]在概率度量空间中得到一类平方型映象的公共不动点的存在性.本文在模糊度量空间中研究一类积分型压缩映象不动点的存在性，证明了若干新的公共不动点定理，从而改进和推广了文献[10-14]的相应结果.

定义1[5]称映象*：[0，1]×[0，1]→[0，1]为连续t-范数，如果其满足以下条件：

（1）*是可结合和可交换的；

（2）*是连续的；

（3）∀a∈[0，1]，a*1=a；

（4）∀a、b、c、d∈[0，1]，若a ＜c，b ＜d，则有a*b≤c*d.

定义2[6]称三元组（X，M，*）为一模糊度量空间，若X 是非空集合，*是连续t-范数，M 是X×X×（0，+∞）上的模糊集，且∀x、y、z∈X 和t、s ＞0，以下条件成立：

（1）M（x，y，t）＞0；

（2）M（x，y，t）=1 当且仅当x=y；

（3）M（x，y，t）=M（y，x，t）；

（4）M（x，y，t）*M（y，z，s）≤M（x，z，t+s）；

（5）M（x，y，·）：（0，+∞）→[0，1]是连续的.

若（X，M，*）为一模糊度量空间，称（M，*）为X 上的模糊度量.

例1设（X，d）是度量空间，∀a、b∈[0，1]，用a·b 表示通常的乘法，在X×X×（0，+∞）上定义函数则（X，Md，·）是一模糊度量空间，称其为标准模糊度量空间，并且称（Md，·）为d 诱导的标准模糊度量.

定义3称三元组（X，M，*）为非Achimedes 模糊度量空间，若（X，M，*）是一模糊度量空间，*是满足下列条件的*-范数.

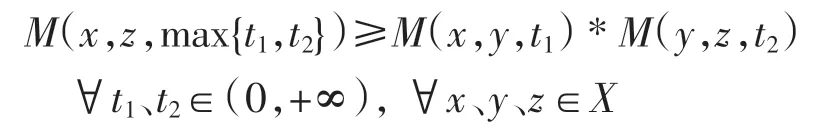
定义4[6]（1）模糊度量空间（X，M，*）中序列{xn}收敛于x 当且仅当M（xn，x，t）→1（n→∞）.

（2） 称模糊度量空间（X，M，*）中序列{xn}为Cauchy 序列，如果∀r∈（0，1）和t ＞0，存在n0∈N，使得M（xn，xm，t）＞1-r，n、m≥n0.称模糊度量空间（X，M，*）为完备的，如果其每个Cauchy 序列{xn}在X 中均收敛.

定义5[11]设（X，M，*）为模糊度量空间，称模糊度量M 为三角的，如果∀x、y、z∈X，∀t ＞0，有

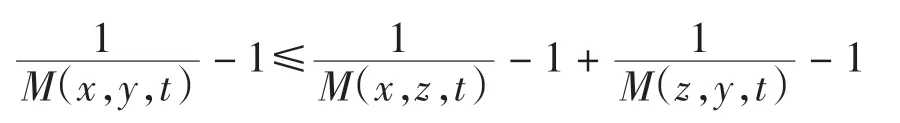
由定义5 知每个标准模糊度量（Md，·）都是三角的.

设Ω={g|g： [0，1]→[0，+∞）连续且严格递减，g（1）=0}.

定义6称模糊度量空间（X，M，*）为（C）g型的，如果存在g∈Ω，使得∀x、y、z∈X，∀t ＞0，有

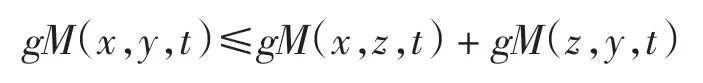
注如果M 是三角的，取则（X，M，*）是（C）g型的.反之未必成立.

定义7称模糊度量空间（X，M，*）为（D）g型的，如果存在g∈Ω，使得∀s、t∈[0，1]，有g（s*t）≤g（s）+g（t）.

引理[16]（1）如果非Achimedes 模糊度量空间（X，M，*）是（D）g型的，则（X，M，*）是（C）g型的.

（2）如果（X，M，*）是非Achimedes 模糊度量空间，*≥*1，其中a*1b=min{a，b}，则（X，M，*）是（D）g型的，其中

2 主要结果

定理1设（X，M，*）为完备（C）g型模糊度量空间，f、h 是X 上的自映象，满足下列不等式

其中：x∈X，t ＞0；α、β、γ、μ 为非负实数且α+2γ ＜1，β+2μ ＜1；φ：R+=[0，+∞）→R+是Lebesgue 可积与可和的，即

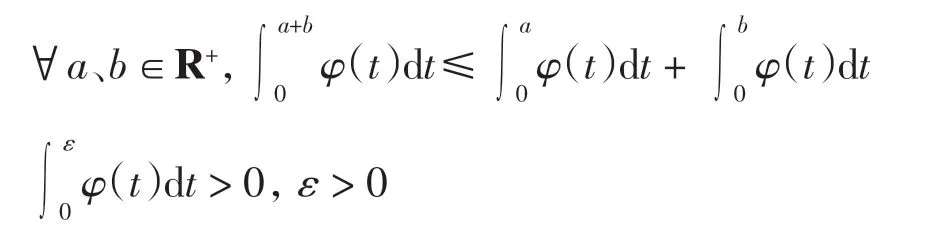
如果f 或h 连续，则f 与h 在X 上有一公共不动点.

证明对x0∈X，可归纳定义序列{xn}为x2n+1=fx2n，x2n+2=hx2n+1，n=0，1，2，…，注意到如果对某个n，有xn=xn+1，则xn是f 与h 在X 上一公共不动点.事实上，如果对某个n，有x2n=x2n+1，则x2n是f 的一不动点.由式（2）有

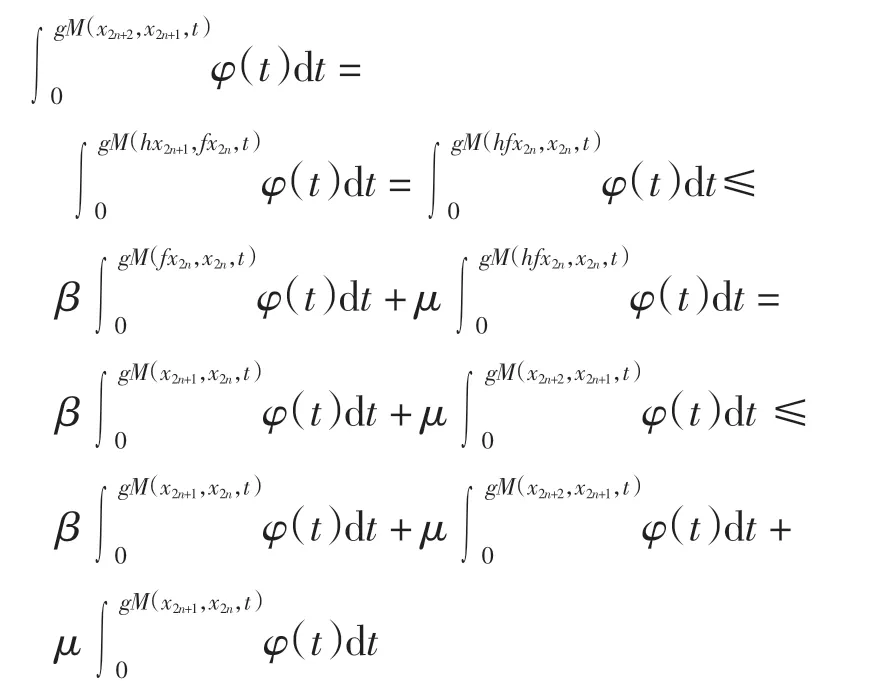
从而

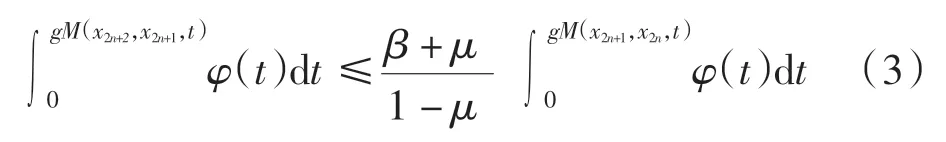
类似地，由式（1）可得

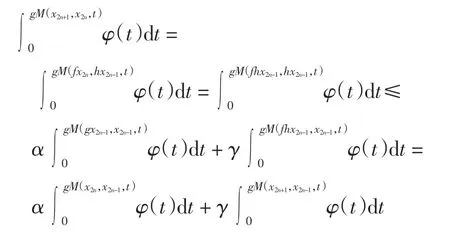
从而

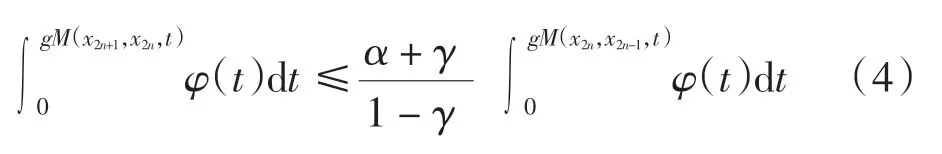
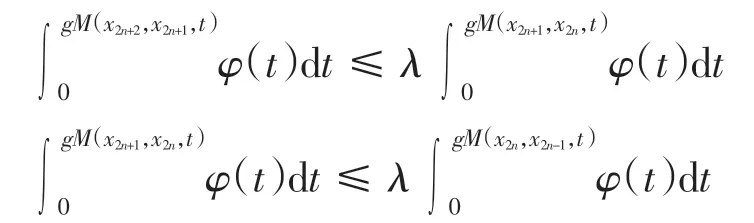
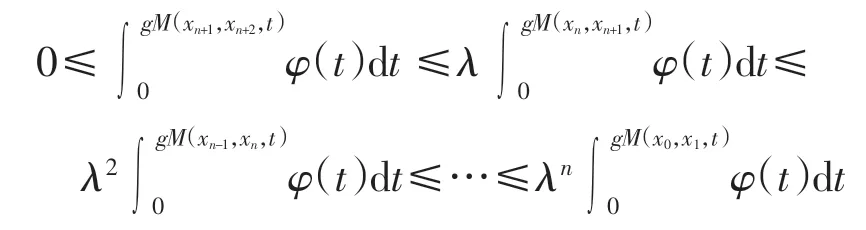
于是∀n、m 和t ＞0，有

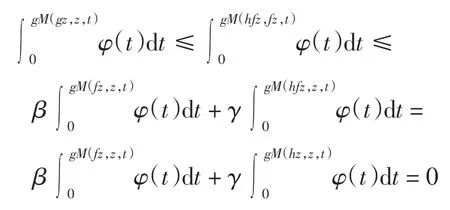
从而

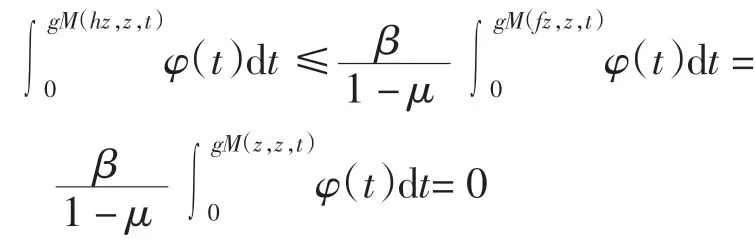
推论1设（X，M，*）为完备（C）g型模糊度量空间，f 是X 上的自映象，满足

其中：x∈X，t ＞0，λ ＜1； φ： R+→R+是Lebesgue 可积与可和的.如果f 连续，则f 在X 上有一不动点.

取φ（t）=1，由定理1 可得推论2.

推论2设（X，M，*）为完备（C）g型模糊度量空间，f、h 是X 上的自映象，满足

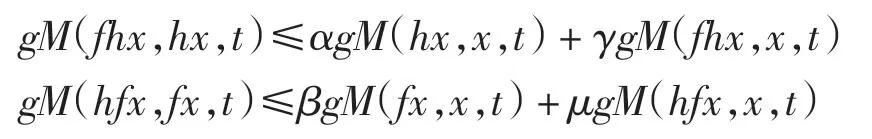
其中：x∈X，t ＞0，α、β、γ、μ 为非负实数且α+2γ ＜1，β+2μ ＜1.如果f 或h 连续，则f 与h 在X 上有一公共不动点.

设（X，M，*）为非Achimedes 模糊度量空间，如果取连续t-范数为a*b=min{a，b}，则由引理知（X，M，*）是（D）g型的，其中进而它也是（C）g型的，于是由定理1 可得定理2.

定理2设（X，M，*）为完备非Achimedes 模糊度量空间，其中连续t-范数为a*b=min{a，b}，a、b∈[0，1），f、h 是X 上的自映象，满足

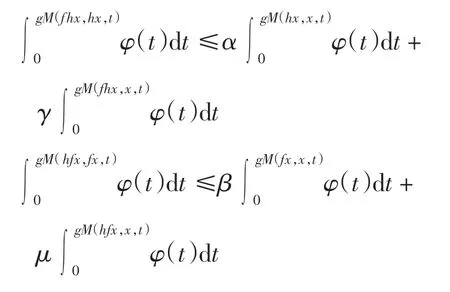
其中：x∈X，t ＞0；α、β、γ、μ 为非负实数且α+2γ ＜1，β+2μ ＜1；φ：R+→R+是Lebesgue 可积与可和的.如果f 或h 连续，则f 与h 在X 上有一公共不动点.

定理3设（X，M，*）为具有M 三角完备的模糊度量空间，f、h 是X 上的自映象，满足下列不等式

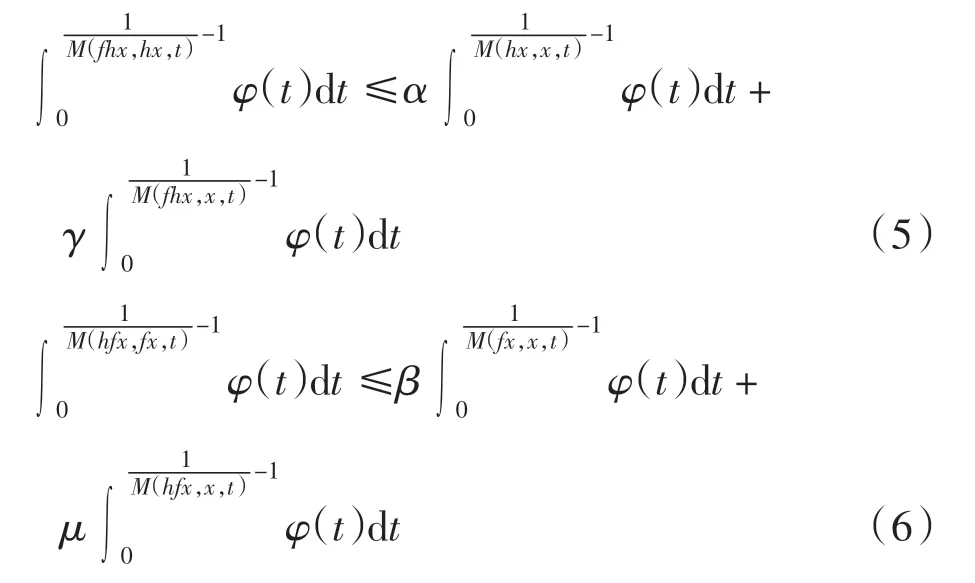
其中：x∈X，t ＞0；α、β、γ、μ 为非负实数且α+2γ ＜1，β+2μ＜1；φ：R+→R+是Lebesgue 可积与可和的.如果f或h 连续，则f 与h 在X 上有一公共不动点.

证明因为M是三角的，取则（X，M，*）是（C）g型的.由定理1 可知定理3 成立.证毕.

推论3设（X，d）为完备度量空间，f、h 是X 上的自映象，满足

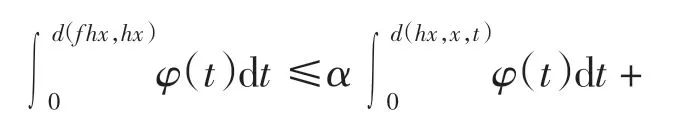
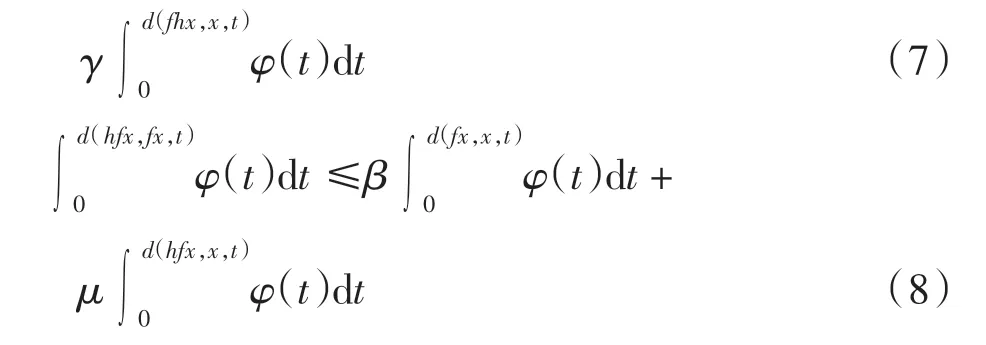
其中：x∈X，t ＞0；α、β、γ、μ 为非负实数且α+2γ ＜1，β+2μ＜1；φ：R+→R+是Lebesgue 可积与可和的.如果f或h 连续，则f 与h 在X 上有一公共不动点.

如果M 不是三角的，取连续t-范数为a*b=min{a，b}，则有如下结果.

定理4设（X，M，*）为完备模糊度量空间，连续t-范数为a*b=min{a，b}，a、b∈[0，1]，f、h 是X 上的自映象，满足

其中：x∈X，t ＞0；α、β、γ、μ 为非负实数且α+2γ ＜1，β+2μ＜1；φ：R+→R+是Lebesgue 可积的，且0，ε ＞0.如果f 或h 连续，则f 与h 在X 上有一公共不动点.

证明对x0∈X，可归纳定义序列{xn}为x2n+1=fx2n，x2n+2=hx2n+1，n=0，1，2，…，取由式（9）、式（10）和定理1 的证明过程可得，对n=1，2，3，…及t ＞0，有

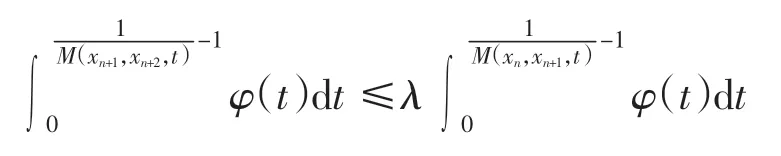
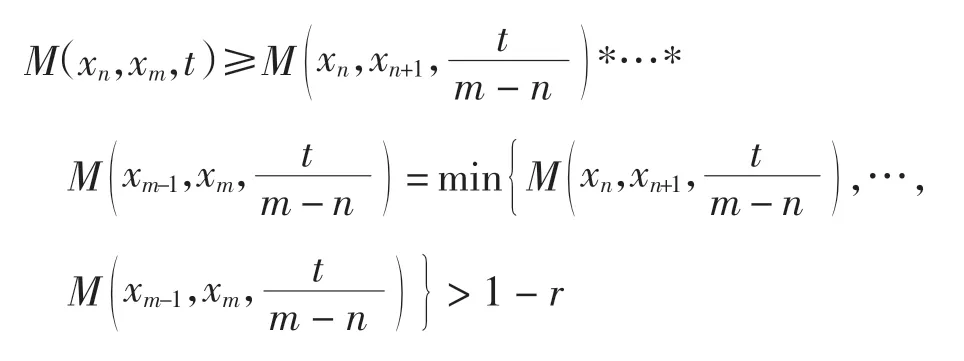
这表明{xn}是完备模糊度量空间（X，M，*）中的Cauchy序列.因此由类似于定理1 的证明过程，可得f 与h在X 上有一公共不动点.证毕.

推论4设（X，M，*）是完备模糊度量空间，连续t-范数为a*b=min{a，b}，a、b∈[0，1]，f 是X 上的自映象，满足

其中：x∈X，t ＞0，λ ＜1；φ：R+→R+是Lebesgue 可积的，且如果f 连续，则f 在X 上有一不动点.

例2∀t∈R+=[0，+∞），取φ（t）=2t，则φ：R+→R+是Lebesgue 可积的，且设X=R，a*b=min {a，b}，a、b∈[0，1].对x、y∈X，t ＞0，定义则易知（X，M，*）为完备的模糊度量空间.对x∈X，定义f、h：X→X 为fx=则有