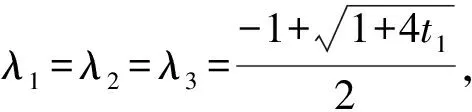两道分点线三角形面积竞赛题的推广

(常熟理工学院数学与统计学院,江苏 常熟 215500)(常熟外国语学校,江苏 常熟 215500)

2018年青少年数学国际城市邀请赛和2001年普特南数学竞赛中有两道求面积的竞赛题，都涉及到分点线三角形[1-2].三角形顶点与对边分点的连线称为三角形的分点线，由三角形3条分点线围成的三角形称为分点线三角形.笔者在题目给定的条件下解出了答案，接着考虑削弱条件后，看看能有什么结论，并把问题推广到一般情况.

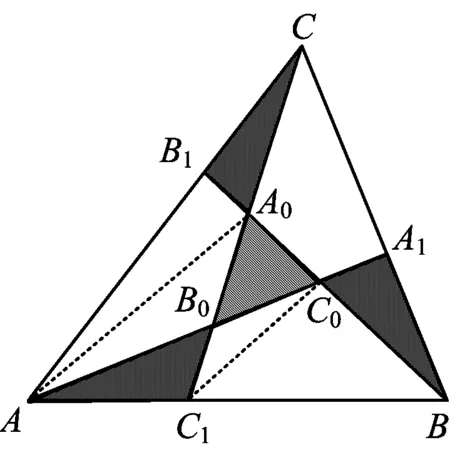
图1

例1一个三角形被分割成4个小三角形与3个四边形，如图1所示，每个小三角形的面积都为1 cm2.请问四边形CA0C0A1的面积为多少cm2?

(2018年青少年数学国际城市邀请赛队际赛第8题)

解联结AA0，C1C0.由S△AB0C1=S△A0B0C0，得S△AC1A0=S△AC0A0，从而

C1C0∥AA0，

同理可得

B1B0∥CC0，A1A0∥BB0,

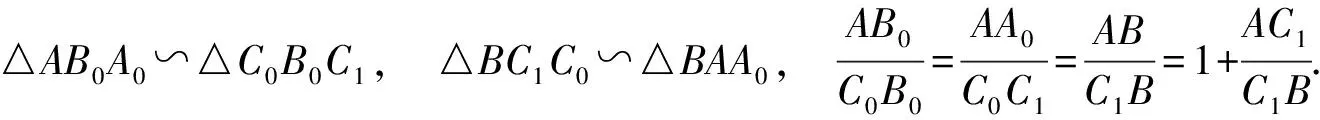
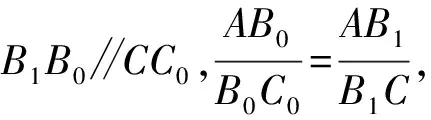
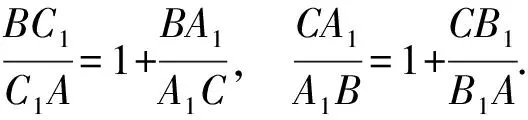
设点A1,B1,C1分别内分线段BC,CA,AB所成的比为正数a,b,c,则上面3个式子变为

消去b,c得

a2+a-1=0，

故3个四边形面积都相等.设四边形CA0C0A1的面积为xcm2，则

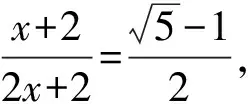
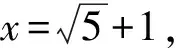
解答本题后再进一步思考，如果在条件中除去小△A0B0C0，而其余3个小三角形的面积相等，又会有怎样的结果呢？

例2如图1所示,在△ABC中，设点A1,B1,C1分别内分线段BC,CA,AB所成的比为正数a,b,c，△ABC的面积为Scm2，AA1,BB1,CC1围成△A0B0C0，当△AB1C1，△BA1C1，△CB1A1的面积相等时，求△A0B0C0的面积.

解△ABA1被直线C1B0C所截，由梅涅劳斯定理得

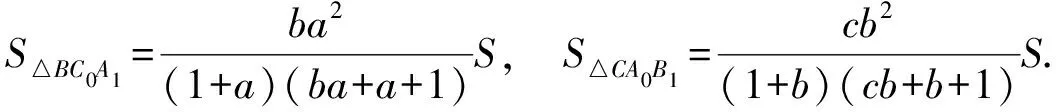
由3个小三角形等积，得连等式

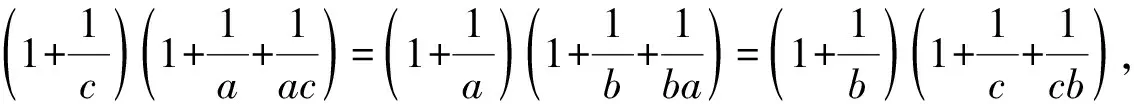
这两个连等式是关于字母a,b,c的轮换对称式，因此猜想连等式成立时，有a=b=c.

下面用反证法证明这一结论：假设a≥b≥c(两个等号不同时成立，下同)，由a,b,c为正数知

综上所知，当3个小三角形等积时，a=b=c.

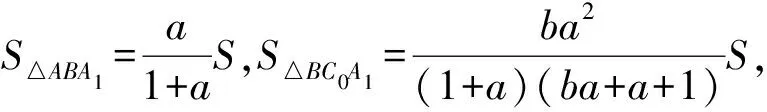
又S△A0B0C0=S-S△ABC0-S△BCA0-S△CAB0，经过运算得

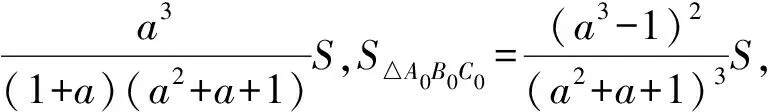
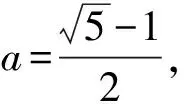
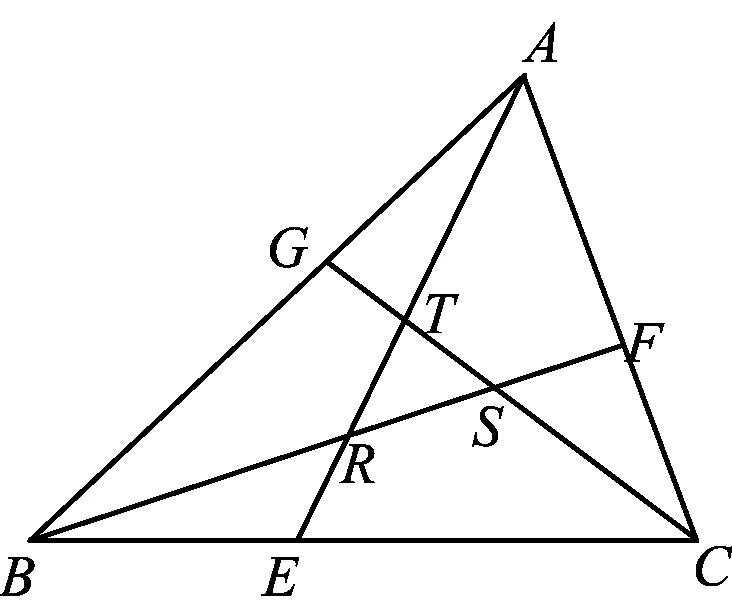
图2

例3如图2所示，已知△ABC的面积为1，点E,F,G分别在边BC,CA,AB上，AE平分线段BF于点R，BF平分线段CG于点S，CG平分线段AE于点T，求△RST的面积.

(第62届普特南数学竞赛A-4题)

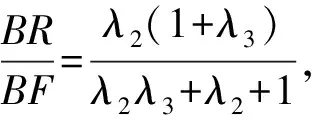
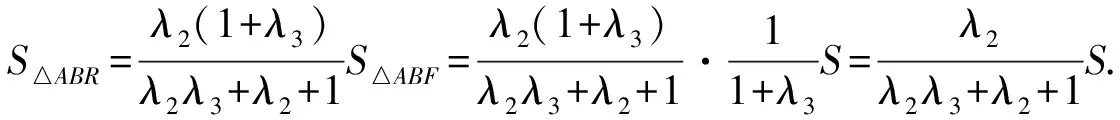
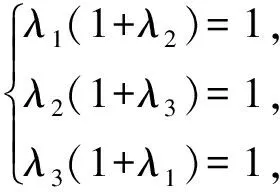
λ1λ2+λ1+1=λ2λ3+λ2+1=λ3λ1+λ3+1=2,

本题通过设三角形各边上的点得到边所分成的比，再利用已知的中点条件代入，求出这些比值，从而计算出所求三角形的面积.可以考虑如果R分BF，S分CG，T分AE所成的比是任意比，并且各不相同，那么如何算出△RST的面积呢？下面来探究这个问题.

解与前面例3的过程相同，在△BCF中，由梅涅劳斯定理可得t1=λ1(1+λ2)，同理可得

t2=λ2(1+λ3)，t3=λ3(1+λ1).

解方程组

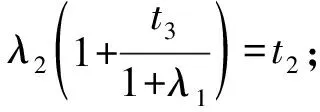
(4)

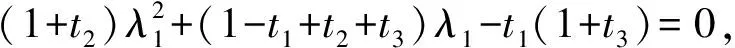
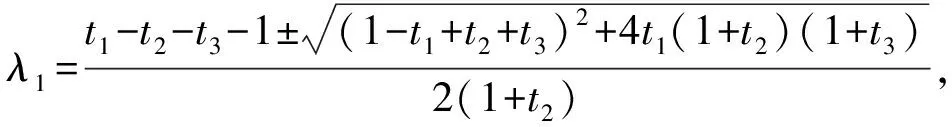
当上式的根号前取负号时，λ1为负数，不符合题意故舍去.同理可得

将解方程得到的λ1,λ2,λ3的值代入上式，即可求得△RST的面积.