基于径向分布函数的杨梅素溶解性模拟

孙芸芸，刘玉智 ，李 剑，陈立宗，陈 辉，郝翠 ，程 燕 ，李赛钰,*

(1.山东蓝城分析测试有限公司，山东 济南 250102；2.齐鲁工业大学(山东省科学院)，山东省分析测试中心，山东 济南 250014)

杨梅素，CAS NO.529-44-2，分子式C15H10O8，英文名为Myricetin(简称MY)，又名杨梅黄酮，属于黄酮类药物。为黄色针状晶体，多存在于蔬菜、水果、草药中。杨梅素具有抗氧化性，常被应用于食品和药物中，此外，研究表明杨梅素还具有抗病毒、抗菌作用和抗癌功效[1-2]。

结晶过程主要在溶液中进行，所以溶液体系的不同对结晶过程会有很大的影响[3]。溶液性质不仅可以通过实验的方式进行表征，同时可以利用分子动力学模拟手段进行辅助表征。径向分布函数(Radial Distribution Function,RDF)在分子模拟过程中常被用来表征溶质与溶剂间的相互作用力。RDF一般用g(r)来表示分子间的距离，分子间距离可以体现分子间作用力的大小[4-5]。分子动力学模拟通过RDF来定性表征溶液的性质近些年来得到了更广泛的认可，该方法对于快速筛选溶剂以及减少实验成本等方面具有独特的优势。

本实验利用Materials Studio 8.0分子模拟软件，基于径向分布函数对难溶性药物杨梅素在水、甲醇等14种常用溶剂中的溶解性进行了模拟预测，旨在简化和指导实验，降低实验和时间成本。

1 建模与计算方法

1.1 模型构建

应用Materials Studio 8.0软件，分别建立杨梅素溶质分子和多种溶剂分子。对所建立的分子进行几何优化，优化采用软件中Forcite模块的Geometry Optimization方法，优化质量为Ultra-fine，本研究中力场选择COMPASS，求和方式选择Ewald。应用Amorphous Cell模块建立周期性盒子，本实验中每个盒子的构建选择1个杨梅素分子和200个溶剂分子(图1)，体系密度设定值与实际溶剂密度相同，模拟温度为298 K。

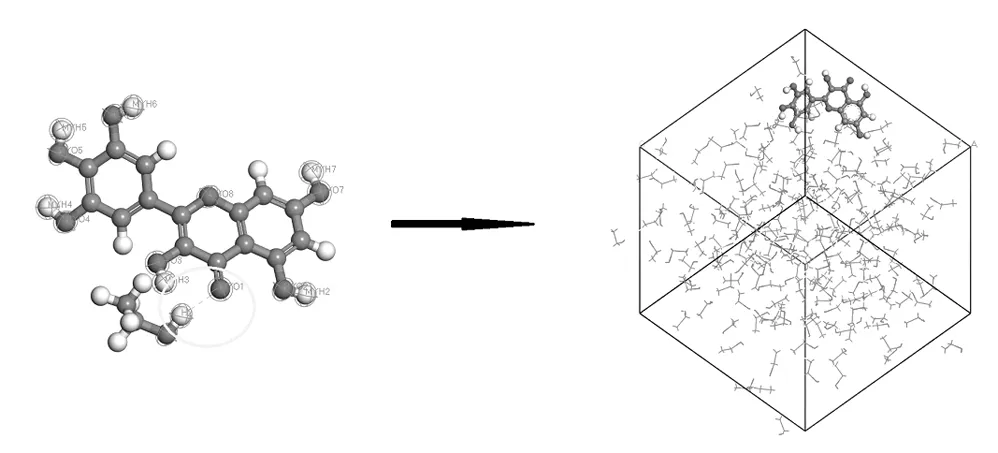
图1 溶液盒子的构建Fig.1 construction of solution boxes

1.2 计算方法

采用Forcite模块的Dynamics方法对溶液盒子进行动力学计算，计算前对溶质与溶剂分子中氢键的供给体和受体进行标记。模拟温度为298 K，选择NVT系宗，静电力求和方式选择Ewald。之后对结果的径向分布函数进行分析，本实验中选取了溶剂分子中电负性较强的O原子或N、S原子进行标定，对溶质分子中的O原子进行标定，以计算分子间的相互作用力，计算过程中截断长度选择10 Å，计算步长为0.2 Å。

2 实验部分

采用高效液相色谱法[2]对杨梅素在正丙醇、正丁醇、异丁醇、仲丁醇和丙酮五种纯溶剂中的溶解度进行测定，测定温度为298 K。模拟选取的溶剂为水、甲醇、乙醇、正丙醇、异丙醇、正丁醇、异丁醇、仲丁醇、丙酮、乙腈、乙酸乙酯、N,N-二甲基甲酰胺、二甲基亚砜和四氢呋喃。溶质与溶剂分子的建模如图2所示。

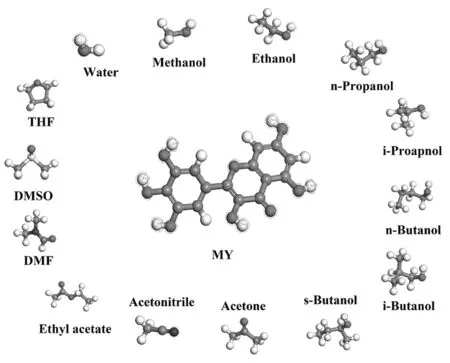
图2 溶质与溶剂分子的建模Fig.2 modeling of solute and solvents molecules

3 结果与讨论

3.1 方法验证

根据已有知识，氢键的作用范围应该在2.6～3.1 Å之间，而范德华力的作用范围应该在3.1～5.0 Å之间[6]，为检验动力学模拟的准确性，首先对乙醇纯溶剂进行模拟，计算结果如图3所示，乙醇分子间作用力分别存在于O*-O*和O*-H*之间，且分别在2.75 Å和1.75 Å之间出峰，与文献[4]数据一致，说明本实验采用的分子动力学模拟方法是可靠的。

图3 乙醇体系径向分布函数Fig.3 RDF of ethanol system

3.2 径向分布函数分析

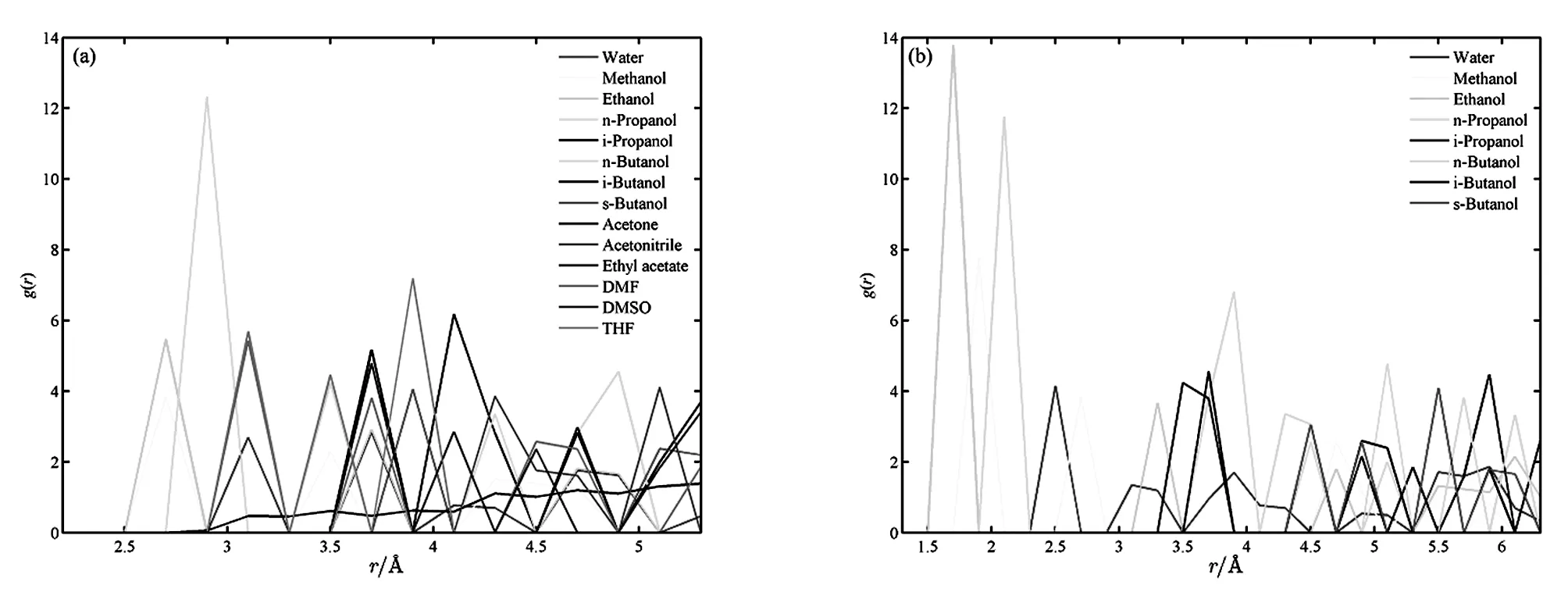
图4 不同溶剂体系中径向分布函数(a - OMY-OSolvent，b-HMY-OSolvent)Fig.4 RDF of different solvent systems(a - OMY-OSolvent,b-HMY-OSolvent)

溶质与溶剂分子之间OMY-OSolvent(图1)的径向分布函数如图4a所示，主峰出现位置在2.6 Å以外，所以溶质与溶剂OMY-OSolvent之间的相互作用力既有氢键作用力，也有范德华力。根据OMY-OSolvent计算得到的作用力大小顺序为正丙醇>异丙醇>THF>乙醇>DMF>异丁醇>乙酸乙酯>正丁醇>乙腈>仲丁醇>甲醇>DMSO>水>丙酮。同时可以看出，溶质与甲醇、乙醇、正丙醇径向分布函数的峰主要落在3.1 Å以内，所以说杨梅素分子与甲醇、乙醇、正丙醇溶剂之间的氢键作用力较强。而丙酮、DMSO等溶剂中的径向分布函数峰较为平缓且出峰位置对应的原子距离较大，说明这几种溶剂中仅存在相互作用力较弱的范德华力。溶质与溶剂之间的相互作用力越大，则理论上溶质的溶解度应当越大，同时，溶质分子之间通过有序排列而形成固体所要克服的溶质-溶剂作用力就会越大，固体相对不易结晶析出。

溶质与溶剂分子HMY-OSolvent之间的径向分布函数如图4b所示，其峰值大小顺序为乙醇>正丙醇>甲醇>正丁醇>异丁醇>异丙醇>水>仲丁醇。根据实验测得的杨梅素在298 K下的摩尔溶解度(单位mol溶质/mol溶液)顺序为仲丁醇(33.14)>正丙醇(24.13)>异丁醇(13.46)>正丁醇(10.20)>丙酮(9.30)。模拟数据除仲丁醇之外，结果跟溶质与溶剂分子之间OMY-OSolvent的径向分布函数顺序较为接近。虽然模拟并不能完全取代实验，但是就杨梅素溶解性质判定而言，采用OMY-OSolvent的径向分布函数来预测溶质在不同溶剂中的溶解性具有指导意义。

溶解性数据是工艺优化过程溶剂筛选和药物分析检测过程中溶剂选择的重要指标，对于类似THF、DMSO等溶剂，不仅存在溶剂本身毒性较大的弊端，而且该类溶剂常常会使得药物在溶剂过程中发生变质或者溶剂化作用，进而导致实验操作的困难性显著增大。因此，采用分子动力学模拟技术对溶解性质进行预测对于简化实验和指导实验具有实际价值。

4 结论

采用分子动力学方法，基于径向分布函数对杨梅素在水、甲醇、乙醇、正丙醇、异丙醇、正丁醇、异丁醇、仲丁醇、丙酮、乙腈、乙酸乙酯、N,N-二甲基甲酰胺、二甲基亚砜和四氢呋喃14种常见溶剂中的溶解性质进行了模拟。模拟结果与实验测定的溶解度结果具有较高的吻合性。采用溶质溶剂OMY-OSolvent的径向分布函数来预测溶质在不同溶剂中的溶解性具有指导意义，杨梅素溶解性的模拟顺序为正丙醇>异丙醇>THF>乙醇>DMF>异丁醇>乙酸乙酯>正丁醇>乙腈>仲丁醇>甲醇>DMSO>水>丙酮。分子动力学模拟技术可以对溶解性质进行预测，对简化实验和指导实验具有实际价值。