一个具有平均复杂性的SAT问题

苏 鑫，胡红钢

(中国科学技术大学 中国科学院电磁空间信息重点实验室，安徽 合肥 230026)

0 引言

在计算复杂性理论中，很多问题都是研究在所有输入上求解的复杂性，亦即最坏复杂性。NP完全性是研究最坏复杂性的经典范例。但在考虑复杂性时，分析者通常只对“实践中”出现的问题实例感兴趣，这就需要考虑平均复杂性。人们已经发现，很多基于图论的NP完全问题在“平均图”上很容易求解。如3-COLOR以很高概率可以在线性时间求解。Bollobas对这一领域进行了综述[1]。

为了建立平均复杂性理论，人们定义了分布NP(distNP)类。LEVIN L A证明了distNP完全问题的存在性[2]，但他构造的问题并不是自然的。LIVNE N给出了一个很强的结果，他证明了所有自然的NP完全问题都有平均复杂性的形式[3]。事实上，他利用了NP完全问题的一些性质，构造了问题的合理分布，使其成为distNP完全问题，但不足之处是分布是不自然的。

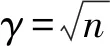
证明SIS的方法是，对于SIVPγ问题的一个输入，格B∈n×n，以连续高斯分布N(0,s2)选取n维向量x1,…,xm，令yi=ximodP(B)，设ai=「q·B-1yi」，以此得到m=O(n2)个向量a1,…,am。若SIS(a1,…,am,q)返回一个短向量e，||e||≤β，则向量是SIVPγ的一个解。

证明LWE的方法是，对于BDDγ问题的一个输入，格B，v∈n，设v=Bs+e，其中Bs是要找的近向量，||e||≤γλ1(B)。以离散高斯分布DB*,r随机选取向量y*，这里，格B*为格B的对偶格。则y*=B*·a。

〈v,y*〉=sTBTB*a+e'

=sTa+e'

(1)

将(a,〈v,y*〉)作为LWE问题的输入，输出得到向量s，则向量B·s即为BDDγ的一个解。

将对于一个NP完全问题是否存在多项式时间算法对值为1的实例给出一个见证并且对值为0的实例给出一个归结辩驳的问题归约到一组SAT实例上，从而构造出一个具有平均复杂性的SAT问题。

(1)本文方法。

考虑一个解决NP完全问题的多项式时间算法，当它的输入为NP完全问题中值为1的实例时，算法输出为t=1，与该问题的一个见证(witness)u；相反；当输入为NP完全问题中值为0的实例时，算法输出为t=0，与一段该问题无解的证明。

xi=f(a1,a2,…,an,s)

(2)

其中i=1,2,…,n。将这n个等式代入输入的实例中可得到x·a=s。相反，输入为子集和问题中无解的实例时，利用复杂性理论中的归结辩驳可得到关于无解的证明。事实上，若coNP完全问题存在多项式规模的归结辩驳时，则NP=coNP。之后，对两种情况取异或运算，便得到两种情况有且只有一种情况成立。这样，可以把对于一个NP完全问题是否存在多项式时间算法对值为1的实例给出一个见证,并且对值为0的实例给出一个归结辩驳，用一组合取范式表示。

注意到，在此方法中，只需要选取的NP完全问题的描述可以用参数表示出来。很多NP完全问题，如顶点覆盖(Vector Cover)、极大团(Maximal Clique)问题，它们的问题描述可以用图的邻接矩阵An×n表示。因此，这些问题也可以用来构造具有平均复杂性的SAT实例。最后，给出一种将SAT问题描述参数化的方法，使得SAT问题本身也可以用来构造具有平均复杂性的SAT实例。

(2)相关的工作。

一方面，有许多工作研究求解随机SAT的算法上，以找到易于求解的SAT问题上[16-18]。另一方面，有很多关于平均复杂性问题的构造。评价一个平均复杂性问题的好坏可以用三个参数衡量：首先，是问题的自然性；其次，是问题所服从分布的简单性；第三，是归约的初始问题的最坏复杂性。将现有结果从这三个角度进行了总结和对比，见表1。SIS、LWE问题和基于图论虽然是不同的组合问题，但通过适当的转换都可以转换成SAT问题(推论1)。因此，也将它们列入表中进行对比，如表1所示。

表1 现有平均复杂性问题的对比

从表1可看出，目前现有的结果有这样的规律：对于基于NP完全问题的构造几乎分布都是复杂的，而对于分布简单的问题它的复杂性几乎都是弱于NP完全问题的。因此，构造出分布简单且复杂性高的平均复杂性问题，对理论和密码学应用都具有很重要的意义。据我们所知，关于SAT平均复杂性的形式只有文献[3]提出过。事实上，通过利用Cook-Levin定理的证明方法，可以将文献[4～15]和文献[17]、[18]中的结果转化为多项式规模的SAT问题(推论1)。因此，也可以将这些结果归入到平均复杂性的SAT问题中。本文亦针对SAT问题，给出一个构造清晰，但基于一个弱于判定NP∪coNP是否等于P的问题，该问题以现有的方法是无法判定的。基于此，提出下面的公开问题，即是否可以构造基于判定NP∪coNP是否等于P的具有平均复杂性的问题。

1 预备知识

本节介绍相关的知识，包括类NP和类coNP的定义、平均复杂性理论及相应的归约，和永真式的归结辩驳。

1.1类NP和类coNP

复杂性类是在特定计算能力上限内能被计算的所有函数的集合。对布尔函数的计算定义了判定问题或判定语言。类P包含了所有可以被高效求解的判定问题，而类NP刻画了可以被高效验证的所有问题。

定义1(类NP)

语言L⊆{0,1}*属于NP，如果存在多项式p(n)和一个多项式时间图灵机M，使得对于任意x∈{0,1}*，有:

(3)

则称u是关于语言L和图灵机M的见证(witness)。

设φ是变量u1,…,un上的一个布尔函数且z∈{0,1}n，则φ(z)表示将φ的变量依次赋予z中各个值之后φ的取值。如果存在赋值z使φ(z)等于1，则称φ是可满足的，否则称φ是不可满足的。如果变量u1,…,un上的布尔函数是在变量或变量的取反上OR操作所得的若干个函数上的AND操作，则称该函数是合取范式(Conjunctive Normal Form，CNF)。

定义2

一个合取范式有如下的形式

(4)

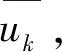
定义3

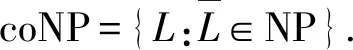
(5)

定理1(Cook-Levin定理)

SAT问题是NP完全问题。

证明：SAT问题显然属于NP，因此，仅需证明它是NP难的。设L是一个NP语言，故存在多项式时间图灵机M使得对于任意x∈{0,1}*，x∈L⟺∃u∈{0,1}p(|x|),M(x,u)=1。不失一般性，可假设图灵机M只有两条带，一条输入带和一条工作/输出带；M是散漫图灵机，即带头移动不依赖带上内容。

设M所有的状态集合为Q，字母表为Γ。M运行到第i步的快照为三元组〈a,b,q〉∈Γ×Γ×Q，其中a、b为带头在两条带上读到的符号，q为此时M所处的状态。第i步的快照记为zi。为了验证zi的正确性，只需查看zi-1,ypos(i),zprev(i)，其中pos(i)表示M在第i步时带头在输入带的位置；prev(i)是M的带头在工作带上在第i步之前最后与第i步在工作带上的位置相同的那个步骤(若第i步的位置是首次访问的，则prev(i)=1)。故存在函数F:{0,1}2c+1→{0,1}c使得：

zi=F(zi-1,ypos(i),zprev(i))

(6)

由于M是散漫图灵机，函数F和这两个下标可以通过平凡输入上模拟M来得到。函数F可以表示长度为c2c的合取范式。因此可以构造满足性与L相同的合取范式，即L可以归约到SAT。

以下是从SIS、LWE等平均复杂性问题到平均复杂性的SAT问题的转换。

推论1

SIS、LWE等平均复杂性问题可以转化为具有平均复杂性的SAT问题。

证明：设M是求解或判定SIS(LWE)问题的多项式时间图灵机。利用定理1中的证明方法，则图灵机M的快照zi=〈a,b,q〉∈Γ×Γ×Q可以用函数式(6)验证，这样可以得到相应的合取范式。由于从SIS(LWE)的实例到相应合取范式的映射是一一对应的，故所得到的也是具有平均复杂性的SAT问题。

1.2 平均复杂性理论

如前文所说，问题对于不同的分布其复杂性也是不同的，因此有如下精确化的定义。

定义4(分布问题)

一个分布问题是一个序对〈L,D〉，其中L⊆{0,1}*是一个语言，而D={Dn}是一系列分布，Dn是{0,1}n上的一个分布。

下面定义分布问题之间的归约。

定义5(平均归约)

称分布问题〈L,D〉平均归约到问题〈L′,D′〉，记为〈L,D〉≤p〈L′,D′〉，指存在多项式时间可计算的映射f和多项式p，q满足：

(1)对任意x∈{0,1}*，|f(x)|=p(|x|)且x∈L⟺f(x)∈L′；

(2)对任意正整数n和y∈{0,1}p(n)，Pr[y=f(Dn)]≤q(n)·Pr[y=f(D′p(n))]。

定理2

如果〈L,D〉≤p〈L′,D′〉且〈L′,D′〉∈distP中，则〈L,D〉∈distP。

证明:假设A′是求解〈L′,D′〉的多项式时间算法，则存在常数C,ε>0使得在任意M上均有

(7)

设f是〈L,D〉到〈L′,D′〉的归约映射，则有判定L的算法A：在输入x上，先计算f(x)，然后输出A′(f(x))。只需证明算法A在服从分布D的所有输入上的平均复杂度是多项式时间。不失一般性，假设在任意x上，|f(x)|=|x|^d。为了完成定理的证明,只需证明

(8)

其中q(n)是分布支配性条件中出现的多项式。根据A的定义和本文的假设条件可知：

(9)

1.3 永真式的归结辩驳

命题逻辑是对两千年来人们常用的推理模式的形式化描述。命题逻辑的主要任务是验证给定的布尔公式是否为永真式或矛盾式。

本文给出归结(resolution)的定义，它可以用来证明给定的公式是矛盾式。令φ是一个n元合取范式，φ的子句分别是c1,c2,…,cm。对于j>m，归结过程将在之前得到的子句c1,…,cj-1上利用如下规则导出子句cj：假设存在变量xi和子句C、D使得xi∨C和xi∨D都是之前导出的子句，则令cj=C∨D。重复上述过程，直到得到关于某个变量xi上的两个矛盾子句xi和xi，归结过程结束。φ的归结辩驳(resolutionrefutation)是指存在上述矛盾的子句序列c1,…,cT，其中c1,…,cm是φ的子句，而cj,j>m，是在c1,…,cj-1上导出的子句。显然，导出的子句都蕴含在之前得出的子句中，故归结是一个可靠的证明系统。如果φ是永真式，则φ存在一个有限长度的归结辩驳，故归结也是完备的。若每个不可满足的布尔公式都存在多项式长度的归结辩驳，则NP=coNP。

证明归结下界的方法目前有瓶颈法与插值方法等。

2 类P中的例子

先从类P中的问题入手，之后再对NP完全问题进行讨论。选择二次方程和线性方程组求解问题，熟知这两个问题有多项式时间求解算法，亦即在类P中。本节先从这两个问题入手，说明多项式时间求解算法的存在性可以用一组多项式规模的合取范式表示。事实上，设变量a,b,c1,c2∈{0,1}，则等式a=b可以用合取范式

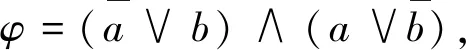
(10)

表示。加法a+b=(c1c2)2，其中(c1c2)2为二进制表示，可以表示为合取范式

(11)

同样地，可以用合取范式表示乘法。根据SAT的完全性证明，一个多项式时间的图灵机可以用多项式规模的合取范式表示。

对于二次方程ax2+bx+c=0，当判别式b2-4ac<0时，算法A输出t=0，并给出ax^2+bx+c=0的归结辩驳：

(12)

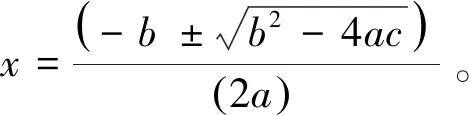
因此，算法A的存在性可以用函数表示为：

∃c1,c2,…,cm,f:[(t=0)∧(c1,c2,…,cm为ax2+bx+c=0的归结辩驳)

⊕[(t=1)∧(x=f(a,b,c))∧(ax2+bx+c=0)]

(13)

进而转化成多项式规模的合取范式。

对于一个线性方程组Ax=b，其中A为n×n的矩阵，x和b为n维向量。为了简化问题的描述，假设(A,b)的秩为n。当行列式|A|=0时，算法A输出t=0，并给出Ax=b的归结辩驳：如果原线性方程组有解，则矩阵A和(A,b)应有相同的秩。

当判别式|A|≠0时，算法A输出t=1，与一个解x=A-1b，这里A-1为矩阵A的逆矩阵。

因此，算法A的存在性可以用函数表示为：

∃c1,c2,…,cm,f:[(t=0)∧(c1,c2,…,cm为Ax=b的归结辩驳)]

⊕[(t=1)∧(x=f(A,b)∧Ax=b)]

(14)

进而转化成多项式规模的合取范式。

3 NP∪coNP与P

本节主要的内容是给出一组合取范式，用来表示对于一个NP完全问题是否存在多项式时间算法A对值为1的实例给出一个见证并且对值为0的实例给出一个归结辩驳。选取NP完全问题子集和问题。子集和问题的一个实例是(a1,a2,…,an,s)，简记为(a,s)。当实例(a,s)无解时，算法A输出t=0，并给出x·a=s的归结辩驳c1,c2,…,cm。当实例(a,s)有解时，算法A输出t=1与一个解x=f(a,s)。因此，算法A的存在性可以用函数表示为：

∃c1,c2,…,cm,f:[(t=0)∧(c1,c2,…,cm为x·a=s的归结辩驳)]

⊕[(t=1)∧(x=f(a,s)∧x∈{0,1}n∧x·a=s)]

(15)

进而转化成多项式规模的合取范式。

定理3

如果可以判定上述SAT问题实例，则可以判断对于一个NP完全问题是否存在多项式时间算法对值为1的实例给出一个见证并且对值为0的实例给出一个归结辩驳。

证明：因为对于可满足实例的函数f和对于不可满足实例的归结辩驳c1,c2,…,cm都是多项式长度的，所以上述SAT问题实例是多项式长度的。

上述实例可满足当且仅当对于子集和问题，存在多项式时间算法A：当实例(a,s)无解时，算法输出t=0，并给出x·a=s的归结辩驳c1,c2,…,cm；当实例(a,s)有解时，算法输出t=1与一个见证x=f(a,s)。又因为子集和问题的NP完全性，所以如果可以判定上述SAT问题实例，则可以判断对于一个NP完全问题是否存在多项式时间算法对值为1的实例给出一个见证并且对值为0的实例给出一个归结辩驳。

4 第3节中合取范式的一些变形

本节给出上一节中构造的合取范式的一个通式和一些变形问题。

4.1 第3节中合取范式的通式

设p∈{0,1}*为NP完全问题的描述中的参数，如第3节中的p=(a,s)。设w(p)∈{0,1}*为NP完全问题的描述中的等式，如第3节中的w(p)为x·a=s。则函数

ψ(w,p)=∃c1,c2,…,cm,f:[(t=0)∧(c1,c2,…,cm为w(p)的归结辩驳)]

⊕[(t=1)∧(x=f(p))∧w(p)]

(16)

为第3节中函数的一个通式，进而转化成相应合取范式的通式。

4.2 基于其他的NP完全问题

通式的构造只要求NP完全问题的描述可以参数化。因此，将子集和问题替换为其他NP完全问题也可以构造表示对于一个NP完全问题是否存在多项式时间算法对值为1的实例给出一个见证并且对值为0的实例给出一个归结辩驳的合取范式。

4.3 kSAT问题的参数化与基于kSAT的构造

这里给出将kSAT问题的实例参数化的方法，这样，可以基于kSAT问题构造合取范式。方法是，列出k-合取范式中可能出现的子句，即所有包含不多于k个文字的子句。之后引入系数pi，i=1,2,…,q(n)。具体地，kCNF中所有可能出现的子句如下：

…

…

对于每个子句，引入系数pj∈{0,1}，j=1,2,…,q(n)，这里q(n)为所有子句的个数，q(n)=O(nk)。将pj与相应子句作“或”运算。参数化的合取范式是这些新的子句作“与”运算，记为Φp。它的构造如下：

…

…

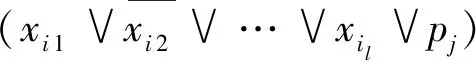
将参数化的合取范式代入前面的通式中，可以得到基于SAT的构造：

ψ(p,Φp=1)

(17)

其中ψ为4.1节中的通式。

4.4 随机化的构造

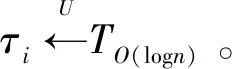
ψ′n=ψn∧τi。

(18)

5 结论

本文给出一个可以归约到判定对于一个NP完全问题是否存在多项式时间算法，对值为1的实例给出一个见证，并且对值为0的实例给出一个归结辩驳归约到一组SAT实例上，从而构造出一个具有平均复杂性的SAT问题。首先给出问题在类P上的类比，之后利用子集和问题给出了构造和证明。同时给出了构造合取范式的通式，使得可以参数化的NP完全问题可以代入通式得到新的合取范式，也给出将SAT问题参数化的方法，从而代入到通式，最后给出了随机化的构造。