剪刀式折叠桥梁展桥机构架桥过程力学状态分析

张 帅，韩 军，涂群章，朱鹏程，杨 旋，张庆宇

(1.陆军工程大学 野战工程学院，江苏 南京 210007； 2.陆军研究院5所，江苏 无锡 214035)

0 引言

无论抗震救灾还是战场环境中都需要一种可以快速架设的桥梁，用以引导人员和装备快速通过障碍，到达预定作业位置。剪刀式折叠桥梁作为一种快速展开式钢桥，主要分为两个状态:一是完全折叠状态，该状态下结构占用空间小，便于存储和运输；二是完全展开状态，该状态下结构稳定，承受荷载，两个状态通过展桥机构进行转换，即架设与撤收过程[1]。

作为一种可重复快速架设与撤收的桥梁,其展桥机构的稳定性与可靠性对整个桥梁的使用性能有着重要的影响[2]。展桥机构在展开过程中受力情况比较复杂，是影响机构稳定性与可靠性的关键因素，对其展开过程进行关键铰点和部件受力分析有着重要的理论意义和工程价值。

展桥机构的研究最多在两个方面，一方面针对不同的使用条件进行新型可展机构的设计[3-4]；另一方面对已经设计的展桥机构进行进一步的优化设计[5-6]。这两个方面都需要进行展桥机构的力学状态分析，进一步进行可展结构的可行性验证或优化结果比较。在可展机构力学状态研究方法方面，最多的方法是采用虚拟样机进行展桥机构的建模以及受力状态的分析[4,6]，虚拟样机建模可以较直观地观察到机构运动过程中的姿态，同时较快地建立模型，这种方法得到了较普遍的应用。文献[7]通过建立理论模型，同时利用虚拟仿真软件进行理论模型正确性的验证，研究了一种精确直线可展机构的力学特性。文献[8]采用数值计算和实验验证的方法进行了可展结构的受力分析。

本文以某型剪刀式折叠桥梁展桥机构展桥过程为研究对象[9],采取D-H矩阵建立其运动学模型[10]，在运动学模型基础上建立静力学模型，进行受力分析,得到剪刀式折叠桥梁展桥机构架桥过程中不同姿态下关键铰点的运动位置和力学状态。分析了其展桥过程中受力特点，为下一步针对性的优化工作打好了基础。

1 展桥机构运动学模型

1.1 剪刀式折叠桥梁展桥机构运动学分析

图1为一种展桥机构运动简图，展桥桥面由两个岸桥节和一个中桥节组成。岸桥节与中桥节由展桥机构进行展开。由于两个展桥机构对称设置，现选取靠近支腿一侧的展桥机构对其进行分析。为了简化模型，将远离支腿的岸桥节和中桥节作为整体考虑，本文统称为中桥节。由两个翻转油缸AB、DF作为驱动力，其中翻转油缸AB控制展桥的收放，翻转油缸DF控制展桥机构的展开和折叠。将支腿设为固定不动来考虑，其机构的自由度为F=3n-2p=3×8-2×11=2。其中n为展桥机构的活动构件数，p为低副约束数。

为了便于分析展桥机构的展开过程，以车辆与支腿的铰接点O0为坐标原点，建立基{W0}坐标系x0O0y0；以支腿与岸桥节的铰接点O1为坐标原点，建立基{W1}坐标系x1O1y1；以岸桥节与中桥节的铰接点O2为坐标原点，建立基{W2}坐标系x2O2y2；以中桥节与展桥机构的铰接点O3为坐标原点，建立基{W3}坐标系x3O3y3，坐标轴的方向如图1所示。设θ1为{W1}坐标系相对于{W0}坐标系的旋转角度；θ2为{W2}坐标系相对于{W1}坐标系的旋转角度；θ3为{W3}坐标系相对于{W2}坐标系的旋转角度。

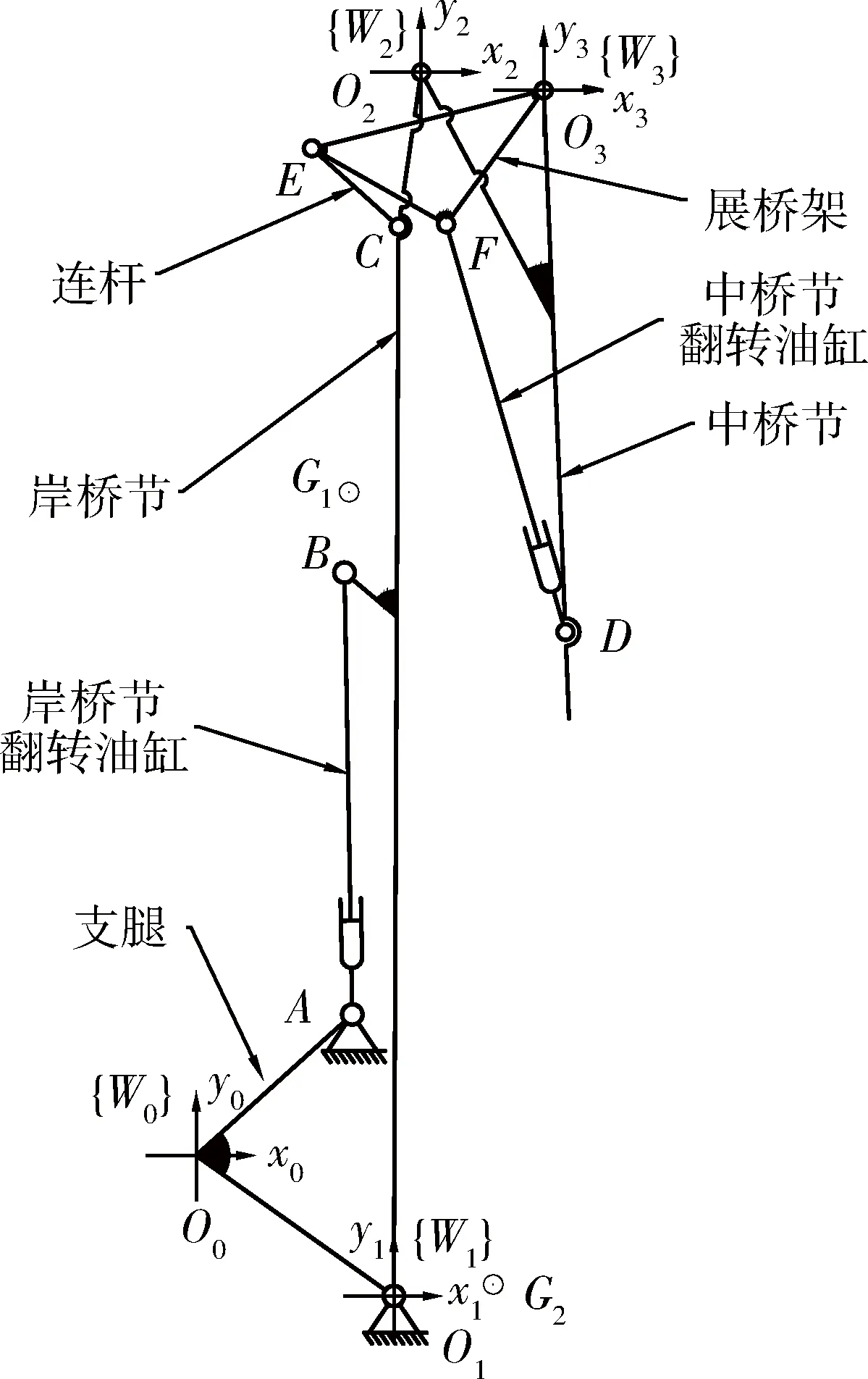
图1 剪刀式折叠桥梁机构运动简图

利用Denavit-Hartenberg法,可建立剪刀式折叠桥梁展桥各个机构间的姿态转换矩阵[11]，为：

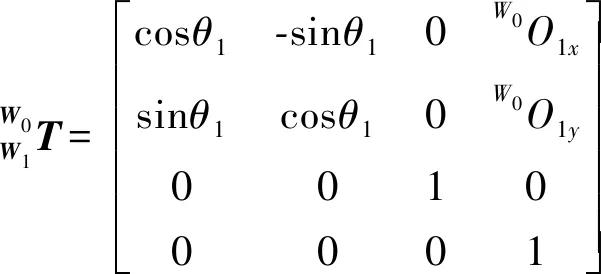
(1)

(2)

(3)

已知点A、O1在基{W0}下的坐标向量为W0A、W0O1；B、C、O2、G1在基{W1}下的坐标向量为W1B、W1C、W1O2、W1G2；D、O3、G2在基{W2}下的坐标向量为W2D、W2O3、W2G2；E、F在基{W3}下的坐标向量为W3E、W3F。则点B、C、O2、D、O3、E、F在基{W0}下的坐标向量分别为：

(12)

1.2 剪刀式折叠桥梁展桥机构几何关系

图2为展桥机构局部几何关系简化图，由于展桥机构具有两个自由度，翻转油缸AB、DF的运动可以完全确定展桥的运动姿态。展桥机构存在θ1、θ2、θ3三个变量，下面建立θ2与θ3的运动学关系。

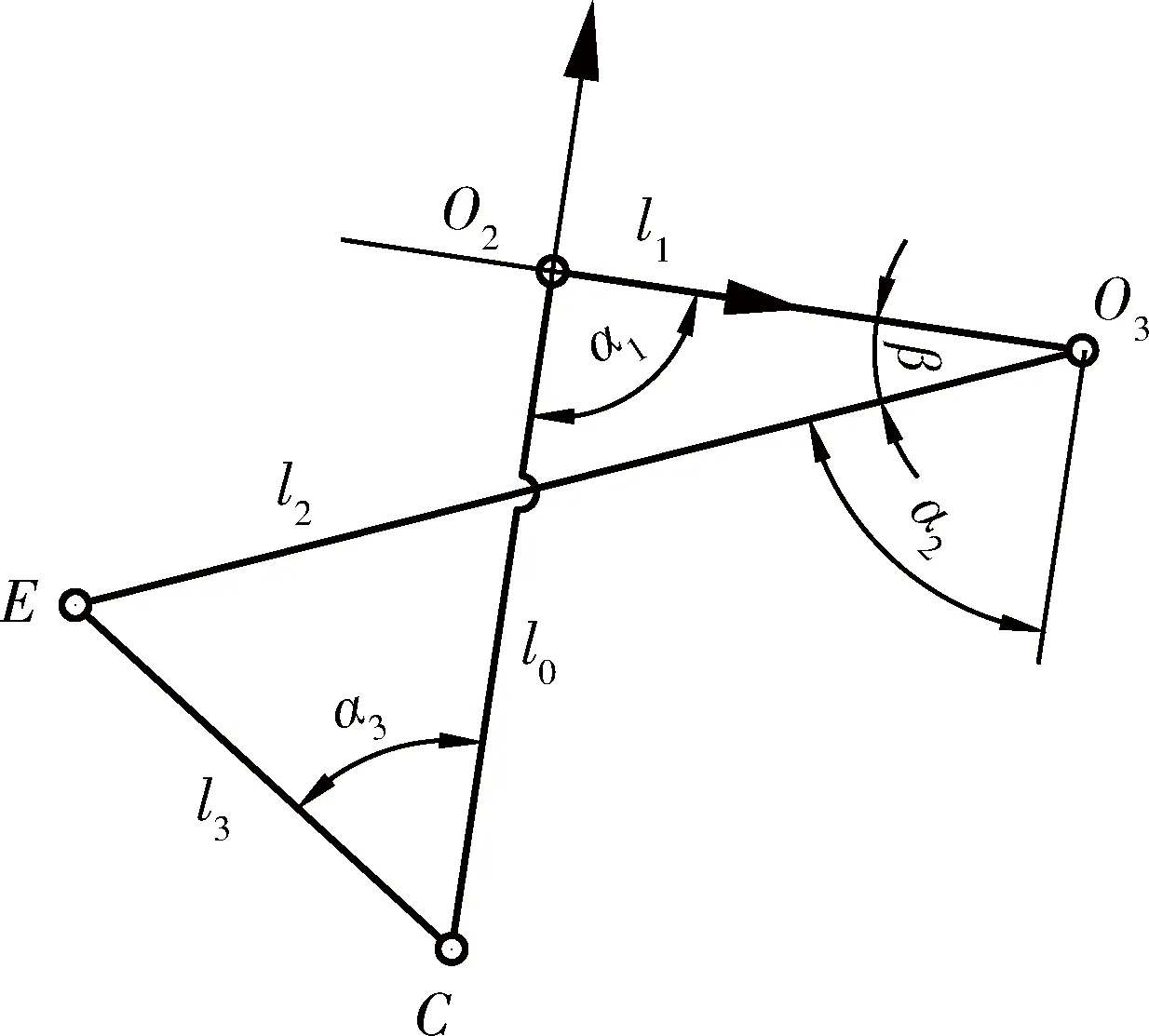
图2 展桥机构局部几何关系

铰点C、O2、O3、E所连接形成的机构，可以简化成一个四连杆机构，设CO2长度为l0,O2O3长度为l1，O3E长度为l2，CE长度为l3。设∠CO2O3为α1，O3E与O2C平行线之间的角度为α2,∠ECO2为α3。对简化四连杆分别在CO2方向和垂直于CO2方向进行投影，建立α1与α3之间的关系CO2方向投影:

l1cosα1+l2cosα2+l3cosα3=l0

(13)

垂直于CO2方向投影：

l1sinα1-l2sinα2+l3sinα3=0

(14)

利用方程(13)、(14)消去α2得到α1与α3的关系。

已知θ1、θ2的情况下，由公式(4)～(6)、(8)～(9)可知，铰点A、B、C、D、O2、O3在基{W0}下的坐标向量均为已知，铰点C、O2、O3由变换矩阵可得到在基{W0}下的坐标向量，分别记为[xcyc01],[xO2yO201]T,[xO3yO301]T。设铰点E在基{W0}下的坐标向量为[xEyE01]T，其中xE、yE为未知参数。

在三角形CEO2中，由余弦定理得：

l02+l32-2l0l3cosα3=(xE-xO2)2+(yE-yO2)2

(15)

同时需满足条件：

l22=(xE-xO3)2+(yE-yO3)2

(16)

l32=(xC-xE)2+(yC-yE)2

(17)

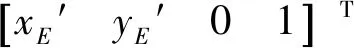
其中EO2′2=(xE′-xO2′)2+(yE′-yO2′)2,EO22=(xE-xO2)2+(yE-yO2)2。

利用由几何关系得到：

θ2=α1-α1′

(18)

如果KO2E>KO3E，则:

θ3=β-β′

(19)

如果KO2E≤KO3E，则:

θ3=-β-β′

(20)

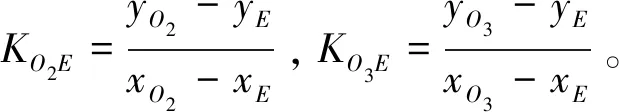
由公式(15)～(20)建立了θ2、θ3的关系，由于展桥机构具有两个自由度，只要确定θ1、θ2的值就可求得各个铰点的空间坐标，展桥机构的运动姿态就可以完全确定。

2 展桥机构力学模型

由于折叠桥展开过程中速度较慢，因此，将展桥机构的力学模型视为静力学模型。

图3为取连杆CE、展桥架、翻转油缸DF和中桥节作为研究对象的受力分析图，以铰点O2为坐标原点，x轴的方向为水平向右，y轴方向为竖直向上，建立坐标系O2xy。其中m1、m2、m3、m4分别为连杆CE、展桥架、翻转油缸DF和中桥节的质量。Fce为铰点C作用力沿铰点C到铰点E方向的分力大小，Fv1为铰点C作用力竖直向上分力的大小。

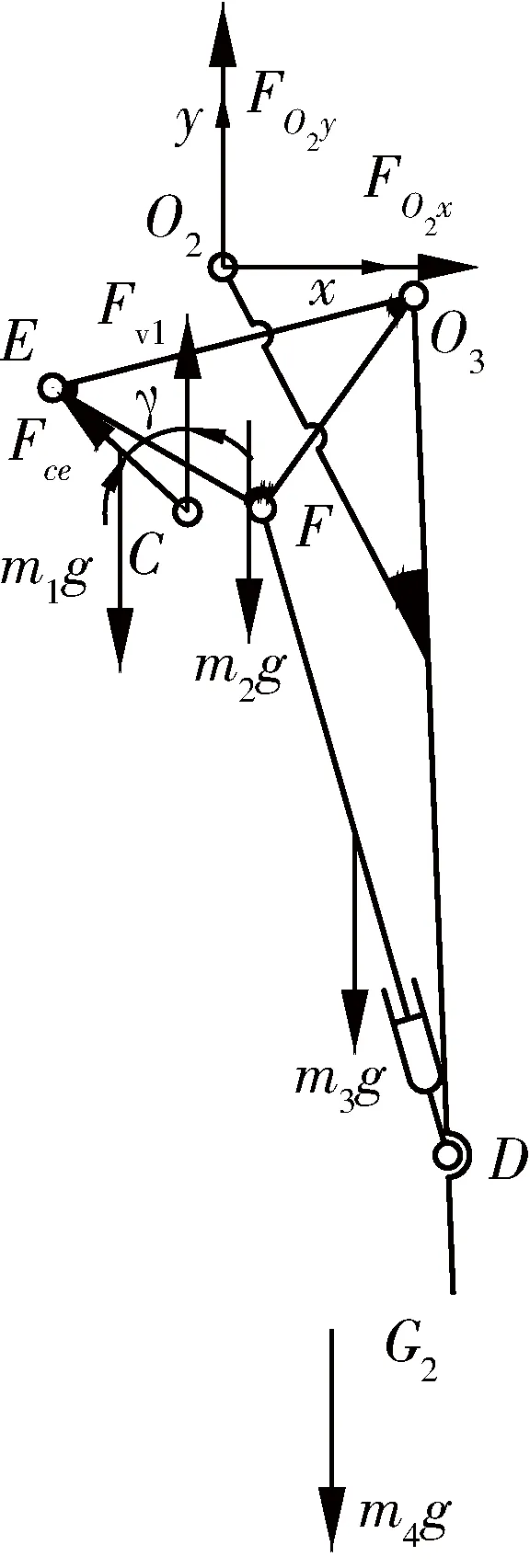
图3 展桥机构局部结构受力

进行不同方向受力平衡分析：

x轴方向受力平衡为：

FO2x-Fcesinγ=0

(21)

y轴方向受力平衡为：

FO2y+Fv1+Fcecosγ-m1g-m2g-m3g-m4g=0

(22)

由力系作用于铰点O2处的力矩平衡条件

(Fv1+Fcecosγ)(xO2-xC)=0

(23)

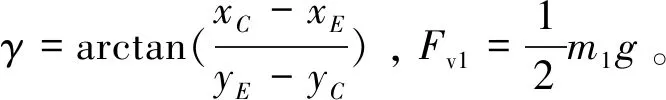
铰点O2受力的绝对值为：

(24)

利用式(21)～(24)通过求解得到Fce、FO2的值。

图4为取连杆CE、展桥架，翻转油缸DF作为研究对象的受力分析图。以铰点O3为坐标原点，x轴的方向为水平向右，y轴方向为竖直向上建立坐标系O3xy。Fdf为铰点D作用力沿铰点D到铰点F方向的分力大小，Fv2为铰点D作用力竖直向上分力的大小。

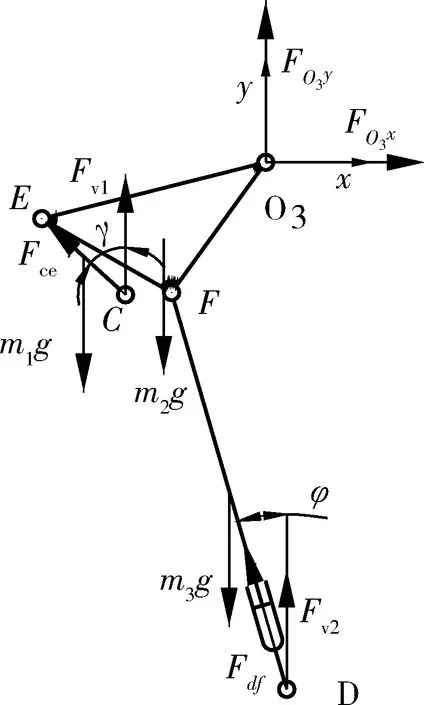
图4 展桥机构局部结构受力

进行不同方向受力平衡分析：

x轴方向受力平衡为：

FO3x-Fcesinγ-Fdfsinφ=0

(25)

y轴方向受力平衡为:

FO3y+Fv1+Fcecosγ-m1g-

m2g-m3g+Fv2+Fdfcosφ=0

(26)

由力系作用于铰点O3处的力矩平衡条件为:

(Fv1+Fcecosγ)(xO3-xC)+

(Fv2+Fdfcosφ)(xO3-xD)+Fce(yO3-yC)sinγ+

(27)

铰点O3受力的绝对值为：

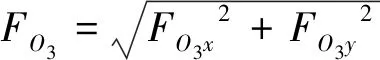
(28)

利用式(25)～(28)求解得到Fdf、FO3的值。

3 展桥过程关键铰点受力状态分析

根据架桥实践，本文拟选取铰点O2、O3、C、E、D、F为关键铰点，分别取θ1为-25°、-40°、-55°,对其进行受力分析。其中θ1=-40°为经验展开角度，实际展开通常在此角度下进行。分析对于不同θ1值，岸桥节与中桥节之间的展开角度θ2由0°变化到180°过程中的关键铰点的受力情况。铰点O2、O3的受力可直接求得，同时通过连杆CE、翻转油缸DF在展桥过程中的受力状态，分别反映铰点C、E和D、F的受力。

利用所建理论模型，采用MATLAB进行建模，得到铰点O2、铰点O3、连杆CE和翻转油缸DF受力状态随θ2的变化图，其中Fce为负时表示连杆CE受拉，为正时表示连杆CE受压。Fdf为负时表示翻转油缸DF受压，为正时表示翻转油缸DF受拉。

图5表明，当θ1=-40°时，铰点O2其初始状态受作用力为9.1×104N，在展桥过程中逐渐减小，θ2变化到33.05°受到最小作用力0.60×104N，再逐渐增加到90.72°受到最大作用力16.8×104N。说明铰点O2在展桥过程中受到大变载荷的作用。同时由图可得，当θ1绝对值较小时，铰点O2在图线两侧受力较小，中部受力较大。

图5 铰点O2受力变化

由图6得到，当θ1=-40°时，O3的受力与O2相似，初始状态时，铰点O3受到18.6×104N作用力。θ2变化到36.36°时不受力，在100.80°受到最大作用力22.3×104N。展桥过程中铰点O3受到大变载荷的作用。同时由图可得，当θ1绝对值较小时，铰点O3在图线两侧受力较小，中部受力较大。

图6 铰点O3受力变化

图7表明,当θ1=-40°时，连杆CE初始状态受压力为10.6×104N,θ2变化到36.50°时连杆CE不受力，90.36°时受到最大拉力15.4×104N。当θ2小于36.50°时，连杆CE受压，θ2大于36.50°时，连杆CE受拉。铰点C、E大变载荷的作用由于存在轴承游隙，力方向的改变对轴承产生的冲击载荷，影响铰点C、E处的轴承寿命。同时连杆CE承受交变力作用。对于图中不同的θ1，当θ1绝对值较小时，连杆CE的承受最大压力较小，承受最大拉力较大。

图8表明,当θ1=-40°时，翻转油缸DF在初始状态的受到最大拉力为27.4×104N，变化到36.50°时其受力为零，θ2在180°受到最大压力16.2×104N，θ2小于36.36°时翻转油缸DF受拉，θ2大于36.36°时翻转油缸DF受压。由于铰点D、F处存在轴承游隙，力方向的改变对轴承产生的冲击载荷，影响D、F铰点处的轴承寿命。由于油液的可压缩性，受力方向的改变加剧架桥过程中桥身的振动，也会对液压系统产生一定影响。对于图中不同的θ1，当θ1绝对值较小时，翻转油缸DF在展桥展开过程中承受最大拉力较小。

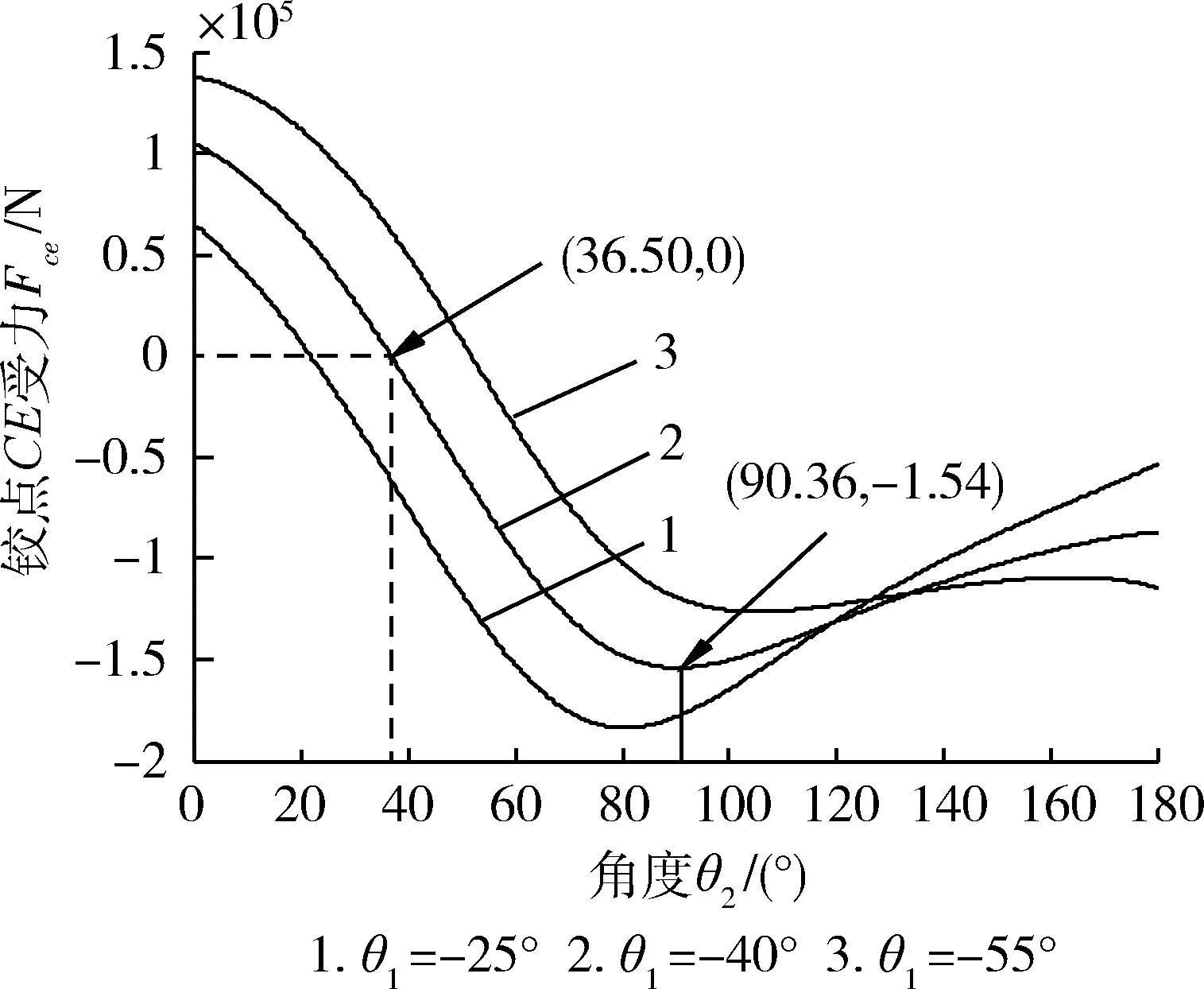
图7连杆CE受力变化

图8 翻转油缸DF受力变化

4 ADAMS验证

4.1 剪刀式折叠桥梁虚拟样机模型建立

采用ADAMS/View模块，按照建立几何模型、添加约束条件、确定质量与重心位置、添加油缸驱动的顺序建立剪刀式折叠桥梁展桥机构的虚拟样机模型[12]，如图9所示。

图9 剪刀式折叠桥梁展桥机构虚拟样机模型

添加驱动时，首先对翻转油缸AB进行驱动，先使θ1由0°分别展开到-25°、-40°、-55°，然后驱动翻转油缸DF，使θ2由0°展开到180°。

4.2 剪刀式折叠桥梁虚拟样机模型仿真

利用所建模型对连杆CE、翻转油缸DF、铰点O2和铰点O3建立受力测量，并利用ADAMS/Post Processor模块进行曲线的后处理。分别生成连杆CE、翻转油缸DF、铰点O2和铰点O3受力随θ2的变化图。

通过图6、图8与图10、图11进行对比可得虚拟样机模型得到的铰点O3、翻转油缸DF受力与MATLAB建立的理论模型所得结果一致，验证了所建的运动学和静力学模型的正确性。

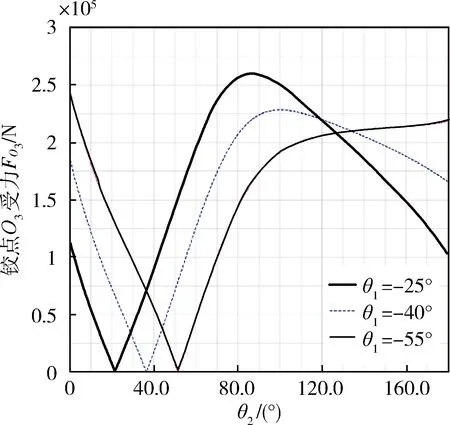
图10 基于虚拟样机模型铰点O3变化情况

图11 基于虚拟样机模型翻转油缸DF受力变化

5 结论

本文以剪刀式折叠桥展桥机构为研究对象，在运动学和力学理论建模的基础上，对其架桥过程中关键铰点的受力特点进行了分析。同时利用虚拟样机验证。得到结论如下：

(1)采用MATLAB进行了理论建模，得到了连杆CE、翻转油缸DF、铰点O2和铰点O3在架桥过程中的力学状态。结果表明，展桥机构关键铰点O2、O3、C、E、D、F在架桥过程中关键铰点处受到冲击载荷和交变载荷的作用。较大压力波动以及冲击与样机时展桥油缸所产生的溢油现象吻合。

(2)利用虚拟样机仿真剪刀式折叠桥梁展桥机构架桥过程的力学状态变化，与理论模型的结果进行对比，结果一致，验证了理论模型的正确性。