“问题”引领思考“串联”达成思维

毛亚玲

[摘  要] 在初中数学教学中，研究如何以“学为中心”，有效设计问题，以“问题串”为主线引领学生思考，启迪学生思维，让学生在问题的思考、解决中不断提高数学学习能力具有重要的现实意义. 文章在分析初中数学问题串设计的主要形式的基础上，结合教学实践，探讨了初中数学问题串设计策略.

[关键词] 学为中心;初中数学;问题串;思维

思维永远是从问题开始，而作为初中数学课堂教学的核心，众多问答式活动所组成的“问题串”不仅能够促使学生主动参与、积极探索数学知识与技能，而且也能有效刺激学生的思维，不断提高学生的数学素养[1]，因此，在初中数学教学中，研究如何以“学为中心”，有效设计问题，以“问题串”为主线引领学生思考，启迪学生思维，让学生在问题的思考、解决中不断提高数学学习能力具有重要的现实意义.

初中数学问题串设计的主要形式

1. 对比式问题串

为了促进学生对新知识的理解、有效发现共性问题，教师应根据问题之间的逻辑关系，设置对比式问题串[2].

例如，在组织学生复习“利用轴对称求最小值”的知识时，笔者及时呈现了教材中的练习题目，即居民区A、B在街道的同一侧，现需要在街道旁修建一个牛奶供应站，则如何修建使得牛奶供应站到居民区A，B之间的距离最短. 实质上该数学问题可以归纳总结为“两点一线”模型，其解题基本思路是利用轴对称性质，因此，笔者设置了如下对比式问题串.

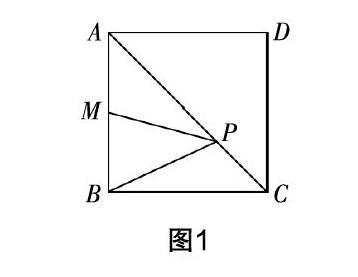
问题1：如图1所示，已知正方形ABCD的边长为1，M为AB的中点，P为对角线AC上的一动点，试求PM+PB的最小值.

问题2：已知A（-4，8），B（2，2）为抛物线y=ax2上的两点，试在x轴上寻找一点Q，使得AQ+QB最短.

设置意图  以上对比式问题串的设计是以教材中原有题目为基础，让学生在问题串的探究中理解问题的本质，有效帮助学生形成分析问题、解决问题的能力和意识.

2. 延伸式问题串

为了达到举一反三、将本原问题与其他相关联领域进行联系，教师应按照总分总的逻辑关系，设置延伸式问题串.

例如，在组织学生学习“二元一次方程组的求解”时，为了能够让学生充分理解二元一次方程的解题方式，笔者设置了如下问题串：

问题1：一元一次方程是如何求解的？

问题2：一元一次方程和二元一次方程有什么区别？

问题3：二元一次方程能否通过一元一次方程进行求解，具体措施是什么？

问题4：你还有哪些问题？

设置意图  通过由浅入深的学习模式，一方面能够激发学生体验合作探究数学问题的乐趣，帮助学生提高解决问题的意识，另一方面，也能帮助学生不断完善自己的知识体系，拓展了学生的思维.

3. 递进式问题串

为了更好地帮助学生掌握知识或方法，教师应按照递进关系，设置延伸式问题串.

例如，在组织学生突破“字母表示数”这一教学难点时，笔者呈现了如下图形（如图2），并设置了以下递进式问题串.

问题1：在圆中，阴影和空白部分之间有什么数量关系？

问题2：字母r表示什么，如何表示圆的面积？

问题3：如果r表示圆的半径，则阴影部分的面积如何表示？

设置意图  从学生原有的知识结构入手，设计环环相扣的问题，引导学生不断思考，从而突破本节课程教学难点.

4. 并列式问题串

为了引导学生在解答相关题目后再总结归纳，发现共性知识，教师应设置并列式问题串. 值得说明的是，这些问题之间并没有先后顺序和主次之分.

例如，在组织学生探究分式概念时，设置了如下并列式问题串.

问题1：已知某一箱苹果重m kg，总售价为p元，则每斤苹果的成本价为多少元？

问题2：开挖一条隧道，若甲施工队单独完成需要a天，乙施工队单独完成需要b天，则共同完成需要几天？

问题3：已知长方形的面积为s，其中一条边长为a米，则另一条边长为多少米？

问题4：观察上述所列出的代数式：，，，思考它们之间有哪些共同特征.

设置意图  引导学生分析和比较分数、分式两者之间的联系与区别，有效培养学生透过现象看本质的思维，培养学生甄别知识之间联系与差别的能力.

5. 發散式问题串

为了促使学生从不同角度研究解决中心问题，促进学生知识的拓展延伸，教师应设置发散式问题串.

例如，在组织学生探究中点四边形时，笔者以任一四边形四边中点围成的四边形与原四边形之间的联系为中心问题，设计了如下问题串.

问题1：如图3、4、5所示，分别以梯形、正方形、平行四边形为例，依次连接各边中点，请问连接后所组成的图形是什么？如何进行证明？

问题2：通过以上问题的探讨，你能猜测出什么结论？能否进一步证明出中心问题的答案.

设置意图  从学生已学内容出发，以任意四边形四边中点围成图形的性质为中心问题，分散出多个小问题，带动学生不断思考.

初中数学问题串设计策略

1. 根据教学情境设置

教师应充分调动学生学习的兴趣，紧紧围绕学生学习与生活，以及熟悉的典型故事有效设置问题串. 例如，在组织学生学习“确定事件与随机事件”时，笔者设置了如下问题串.

在2016年里约奥运会中，A，B两名中国选手进入到最后冠亚军决赛.

问题1：中国能否赢得本场次的冠军？

问题2：A选手是本场次冠军吗？

问题3：如果A选手是外国选手，则问题1、问题2的答案具体是什么？

2. 通过习题、试题改编

教师应加强学生学习知识的连贯性，把相关知识点链接起来，有效实现知识的迁移. 如图6所示，A，B是抛物线y=x2-2x-4与直线y=x的两个交点，M为抛物线上的一动点，试回答以下问题：

问题1：若点M与抛物线顶点相重合，则△OMB的面积是多少？

问题2：点M在抛物线对称轴的右侧，且△OMB的面积等于10，求点M的坐标.

问题3：若以M为圆心，为半径的圆与直线AB相切，求点M的坐标.

3. 通过学生有疑惑的问题进行改编

教师应紧抓学生在课堂或课后提出的问题，引导学生逐步解决一个个小问题，最终达到理清思路的目的，体会知识的生成过程.

例如，当学生提出任一多边形都可以剪拼成矩形这一问题时，笔者层层递进，设置了以下问题串.

问题1：如何把直角三角形剪拼成矩形？

问题2：如何把四边形剪拼成矩形？

问题3：任一多边形都可以剪拼成矩形吗？

总之，不同类型的问题串具有不同的特点，教师应结合教学目标和学生学习的实际水平，通过改编习题、试题、学生提问等方式选择恰当类型的问题串进行教学，只有这样，才能促进学生积极主动的思考、探究，自主建构知识[3]，达到掌握所学的知识点，不断提高学生学习积极性和学习能力的目的.

参考文献：

[1]崔竞. 在解决问题中提升学生的思维品质[J]. 上海中学数学， 2016（10）：38-40.

[2]李婧. 例说初中数学教学中“问题串”设计的“四化”[J]. 中学数学， 2012（5）：19-20.

[3]刘雪琴. 例谈初中数学问题串的教学设计[J]. 初中数学教与学， 2014（4）：21-23.