高次分数阶Laplace方程的Liouville定理

郝 芳,王淑英

(黄河科技学院信息工程学院，河南 郑州 450000)

近年来，分数阶Laplace算子因其在物理[1-2]、金融和概率等方面的广泛应用而备受关注。然而，由于分数阶Laplace算子的非局部性，对分数阶方程理论研究远不如像对整数阶方程的理论研究那么完善。分数阶Laplace算子是一个非局部拟微分算子，定义为

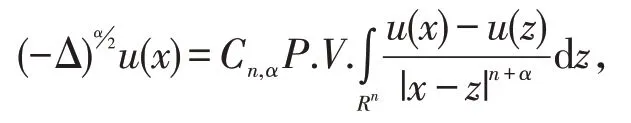
其中α为0与2之间的任意实数，P.V.表示柯西主值。对分数阶方程解的存在性、对称性及正则性研究已有丰富的科研成果。在研究此类方程时，最主要的困难是由于分数阶Laplacian算子的非局部性。为克服此困难，Caffarelli和Silvestre[3]将非局部问题转化为更高一维空间Rn×[0,∞)中的局部问题；后来，Chen，Fang和Yang[4]利用积分形式的移动平面法证明了上半空间中临界和次临界情形下分数阶Laplace方程正解的不存在性；最近，Chen，Li和Li[5]建立分数阶的强极大值原理，对非局部问题采用直接形式的移动平面法。这些方法在研究分数阶Laplace方程发挥着重要作用。

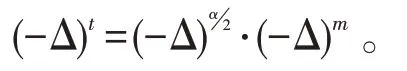
显然，算子(-Δ)t是一个非局部算子，在Schwartz空间有定义。考虑了单位球上的Hénon方程：

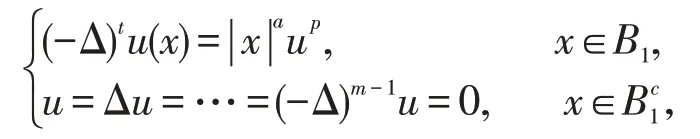
p＞1,a＞0。他们结合分数阶形式的Pohozaev等式和爬山原理证明了超临界情形下弱解的不存在性及次临界情形下弱解的存在性。Li和Zhuo[7]证明了下面高次分数阶方程

正解的不存在性。首先建立方程(1)与积分方程

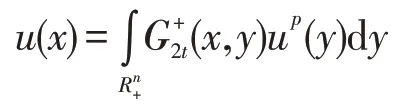
考虑具有Navier条件的高次分数阶方程：

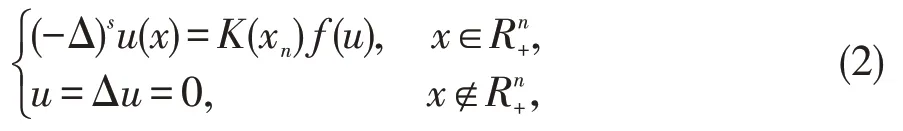
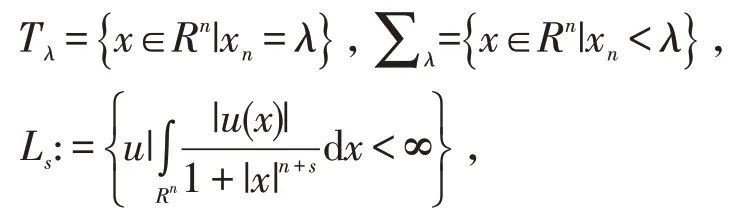
主要结果为：

定理1设H={x∈Rn|0＜xn＜λ,λ∈R}是Σλ内的一个无界区域。设0＜α＜2，且U,V在上下半连续。若

其中c(x)＜0，且当充分大时如果

则存在常数R0＞0，使得|x0|≤R0。

证明由条件（5）得

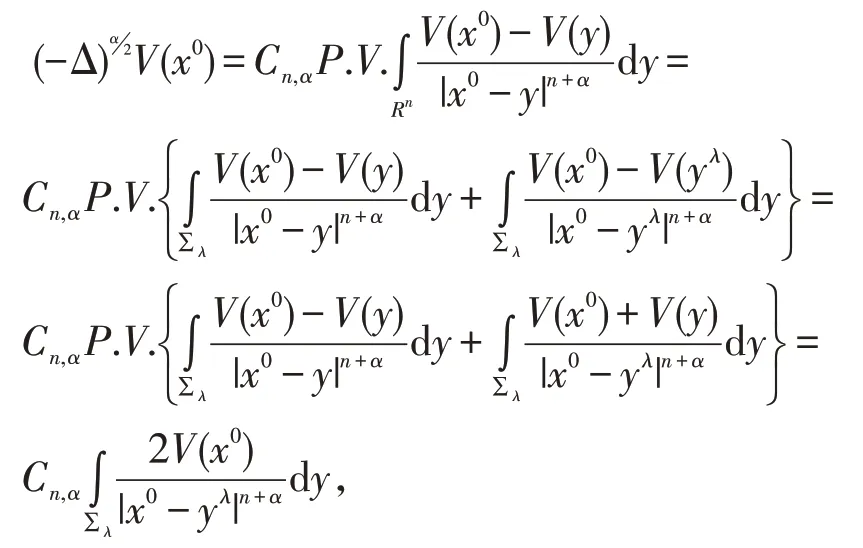
对任一固定的λ，都存在常数C，使得当x0∈H且当x0充分大时，有

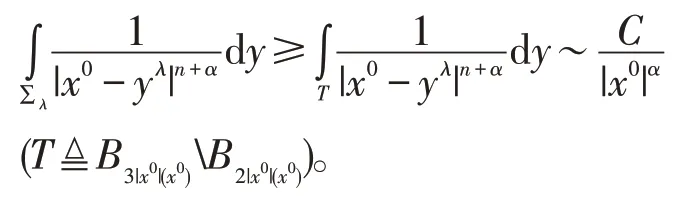
从而，

由c(x)＜0及（5）和（8）可得

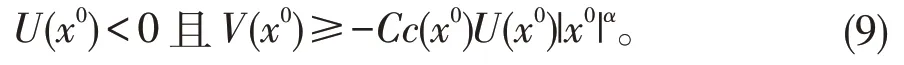
又因U(x)是中的下半连续函数，则一定存在一点x1，使得

从而在ω(x)的负极小点处有

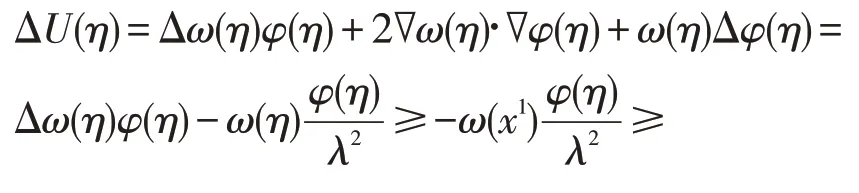
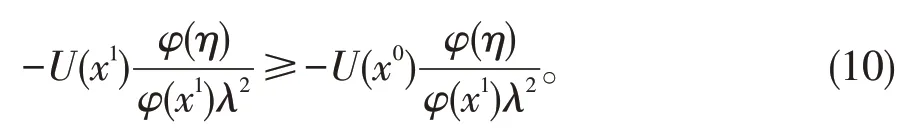
由（3）和（9）可得

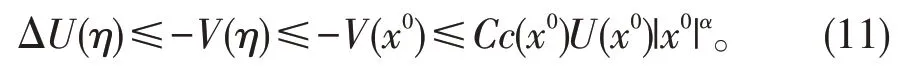
从而由（10）（11）容易推出

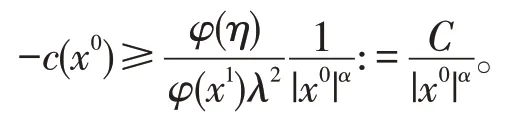
定理2设假设是方程(2)的非负解，且K(xn)和f(t)分别满足：

①K(xn)≥0关于xn非减且局部有界；

②f(t)关于t严格单调递增且

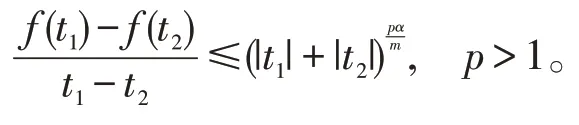
则u(x)≡0。

证明首先阐述定理2证明中所需要的两个引理。

引理1设Γ是Rn中的有界区域。设u∈且在上下半连续。如果函数u满足

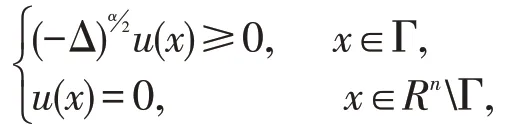
则u(x)≥0,x∈Γ。且若在Γ中某一点有u(x)=0，则u(x)≡0,x∈Rn。在无界区域上，如果此定理仍然成立。

引理2设是有界狭窄区域，不失一般性，假设Ω包含在狭窄区域中，l充分小。考虑方程组

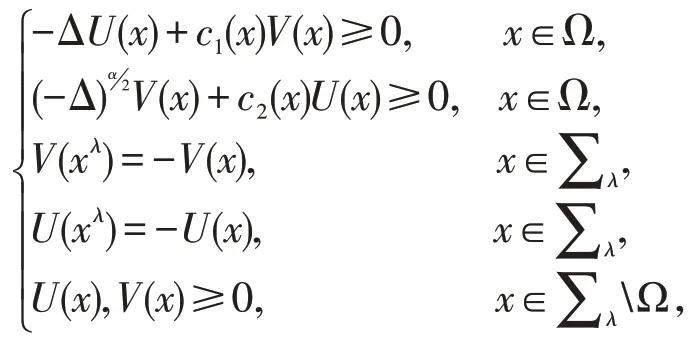
其中ci(x)≤0,i=1,2有界在中下半连续。则当l充分小时，有

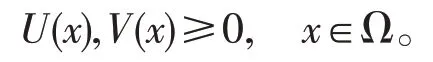
对无界区域Ω，若U(x),V(x)→0,|x|→∞，(3)式仍成立。并且，若存在一点∈Ω，使得或则

证明令-Δu=v，则方程(2)可以写成如下两个方程：

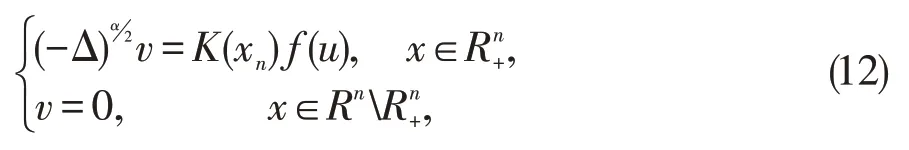
及

记

则

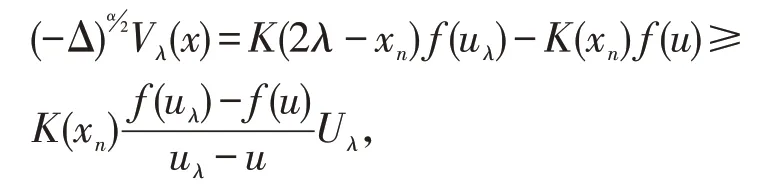
从而

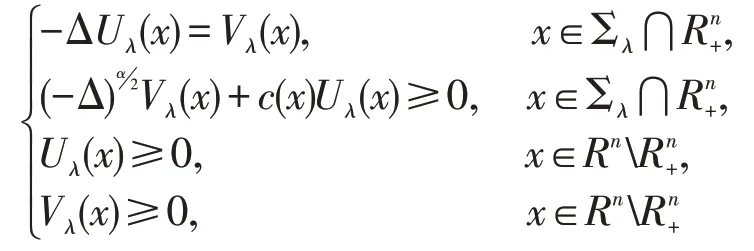
（1）证明当λ充分小时，有

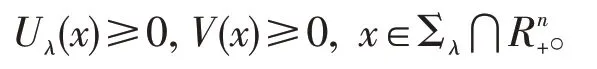
由定理2的①②可知，c(x)有下界且c(x)＜0。当固定λ时，当|x|→+∞时，|xλ|→+∞。从而由可知，u(x)→0,|x|→∞且u(xλ)→0,|x|→∞。所以，当x∈Σλ时，Uλ(x)→0,|x|→∞。

同理，可证Vλ(x)→0,|x|→∞。则当λ充分小时，取引理2中的Ω为为狭窄区域，则

其中，引理2中c1(x)=-1,c2(x)=c(x)。

（2）由(14)式，可以从xn=0附近开始移动平面Tλ，只要Uλ(x)≥0,Vλ(x)≥0成立，则一直向着沿着xn轴移动平面。定义

接下来证明λ0=+∞。

用反证法，如若λ0＜+∞，则必有

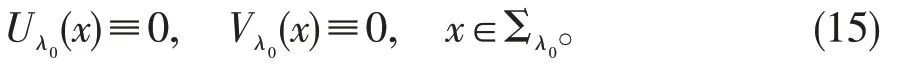
由(15)式可知，平面xn=2λ0是边界关于平面的对称平面。由边界条件及关于的对称性知：在xn=2λ0上有u(x)=0，这与u(x)＞0矛盾。从而λ0=+∞即方程正解u(x)关于变量xn单调增加。这与在无穷远处矛盾，从而方程无正解。

现在证明(15)式成立。假设(15)式不成立，则由强极值原理，

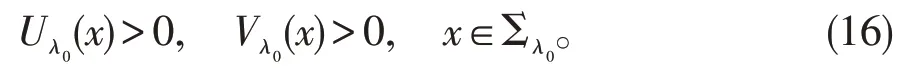
则可以继续沿xn方向移动平面Tλ0，更确切的说，存在一个ε＞0，使得对任意的λ∈[λ0,λ0+ε)，有

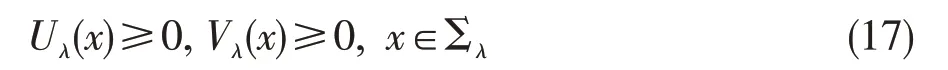
成立。这与λ0的定义矛盾，从而(15)式成立。

接下来,证明(17)式成立。若(17)式不成立，即假设存在点，使得

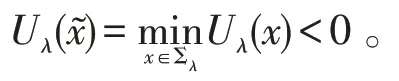
从而存在一点，使得

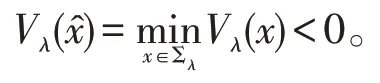
由条件知，

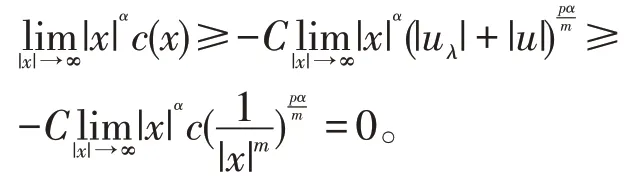
因此，c(x)满足定理1中的条件，从而，存在R0，使得

固定R0，则对任意小的δ＞0，由(16)式知，存在常数C使得

这也就意味着

但由引理2知，在狭窄区域(ΣλΣλ0-δ)∩BR0(0)内，Uλ(x),Vλ(x)≥0。

从而与（18）式矛盾，则必有(17)成立。定理证毕。