基于能量差的电能质量特征提取方法的研究

纪 萍，陈 玲，吴静妹

(河海大学文天学院，安徽 马鞍山 243000）

随着用电量需求的不断增加，一些高性能、高精度、高科技设备的广泛使用，对电能质量提出了更严格的要求。一些非线性设备使用过程中向电力系统注入各种干扰信号，这些扰动信号容易引起设备过热、电机停转、保护失灵以及计量不准等严重后果，造成严重的经济损失和社会影响，对电网的正常运行产生诸多不利影响[1]。电能质量问题日益突出，引起用电供电双方的普遍重视。

影响电网质量的扰动信号主要有：电压上升、电压下降、电压中断、谐波、脉冲、暂态信号、电压闪变[1]。因此，有效分析电网中受到的干扰信号，明确干扰信号的类型，这对电网污染的治理，提高电能质量都是非常有必要积极意义。对扰动信号进行分类识别，关键技术就是有效提取信号的特征向量，目前特征提取的方法有：傅里叶变换，小波变换，S变换等数字信号处理方法。

傅里叶变换及其改进算法作为经典的信号分析方法具有正交、完备等许多优点，适合分析平稳信号[2-4]，后续的研究对傅里叶变换在算法上了做了相应的修改，检测精对有所提高。文献[2]～文献[4]，采用快傅里叶及其改进算法实现对各类谐波平稳信号进行检测，获得较好的检测效果。S变换由于其良好的时频局部性能，但是其对噪声不敏感，计算量大，难以满足实时性要求[5]。小波变换由于具有时频局部化特性，特别适合于非平稳信号分析，小波变换在时-频平面不同位置具有不同的分辨率，是一种多分辨率分析方法[5-7]。因此将小波变换应用于电能质量分析领域具有较大的优点。文献8采用小波技术实现对扰动信号进行检测和分类[8]。文献9采用小波包技术实现对谐波信号的电压和电流信号进行检测[9]。

本文提出一种新的特征向量提取方法，利用小波多分辨对典型扰动信号进行分解，通过帕斯瓦尔定理对含有信号特征的分量进行能量计算，并与纯净的无干扰信号进行能量差，获得新特征向量，送入分类器，通过与现有的方法进行对比，取得较好的分类识别效果。

1 特征提取

1.1 多分辨分解

对于任意信号f(t)要进行多分辨率分解要满足f(t)∈V，Vj是函数空间L2(R)的子空间，在L2(R)空间里的所有函数f(t)是模平方可积的，L的含义是贝勒格积分，“2”表示函数的模平方的积分，“R”表明积分自变量t是实直线上的线，f(t)是这个空间的一个元素。多分辨分析的一个基本要求需要Vj满足以下表达式：…⊂V-2⊂V-1⊂V0⊂V1⊂V2⊂L2空间向量嵌套图形如图1所示。

图1 多分辨空间向量嵌套图

信号f(t)满足上述空间要求，其小波变换公式如下：

其中,i，j为整数，ψi,j为小波变换展开函数，ai,j为信号f(t)小波变换的系数，可以表示为

通过对ψi,j进行运算，可以得到母小波函数ψi,j，

其中，j是时间平移参数，i是尺度指标参数。

要进行多分辨率分解需要满足

其中,h(n)为尺度函数系数的复数序列。利于小波进行MSD尺度分析可以得到：

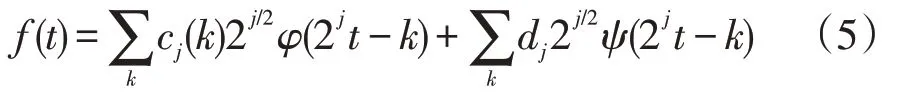
其中,φ表示的是平移尺度函数，ψ表示的小波展开函数。cj表示的是第j层的尺度平移系数，dj表示的是第j层的小波分解系数，可以表示如下：

其中,g(n)和h(n)的关系式：

第一步将信号的谱分为一个低通带h(n)和一个高通带g(n)；第二步将低通的信号分为另外的较低的低通带和另一个高通带，以次类推。其中L代表滤波器的长度，基于小波变换进行MSD分解。信号基本频率为f，L代表滤波器的长度，采集的电压信号的频率为fsp。基于DWT的n层MSD如图2所示，根据MSD原理，以此按照信号的频率进行高低频划分。第一层低频信号范围为0-f/2，高频信号为f/2-f。以此类推，进行n层MSD分解后，每一层的低频信号为0-f/（2n），高频信号为[f/（2n）]-f/2n-1。因此：

式中的cn为分解信号的近似系数，dn为分解信号的细节系数，通过分析每个信号的细节系数，获得各个扰动的信号特征向量值。对信号的高频分量不再分解，而将信号的低频部分继续分解。实际中分解的级数取决于要分析的信号数据特征及用户的具体需要。

图2 多分辨率分解信号分解图

1.2 改进能量差的特征提取方法

利用帕塞瓦尔定理计算小波多分辨分解后的各层能量值，公式10给出信号的能量与每个分量及小波系数的能量关系，公式如下：

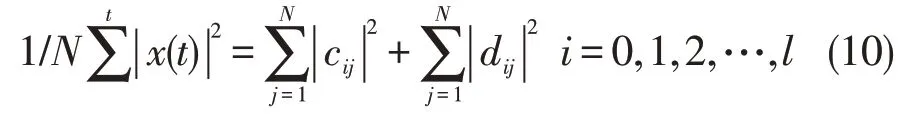
其中,左边信号代表信号x(t)的能量，右边第一项代表分解信号的近似能量，第二项代表分解信号的细节能量，利用第二项公式来确定信号的特征信息。令：

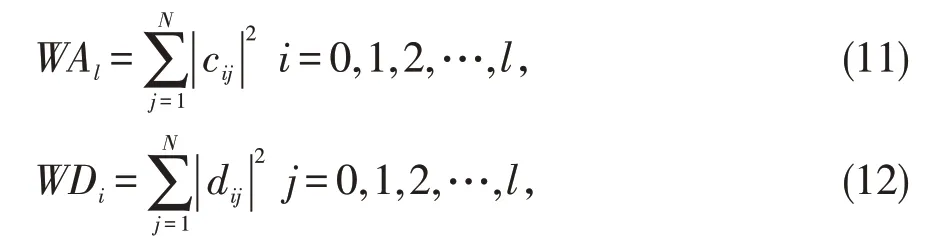
其中，i代表的是信号分解的层数，N代表每一层分解的详细信号系数的个数。WDi代表的是第i层的能量分解系数，WAl是进行MSD分解第l层的近似能量系数。因此，含有扰动信号的l层分解的特征向量可以表示如下：

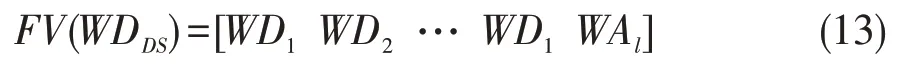
纯净的无噪的电网信号的特征向量可以表示为：

对信号进行多分辨率分解后，计算每层能量值均为正值，为了清晰地提取特征向量，对代表各种扰动信号的特征作进一步的修订。将信号各层的能量值减去如干扰信号的理想电网信号的能量值：获得信号的另一个新特征向量，其中ΔW=WDDS-WDPS，用ΔW作为各类扰动信号新的特征向量。

2 电网扰动信号模型建立

正常电网信号的基本频率为50Hz，归一化幅值为1p.u.。电网中典型的扰动信号为谐波、电压上升、电压下降、电压中断、闪变、暂态震荡，脉冲7种扰动信号，信号模型及其参数见表1。

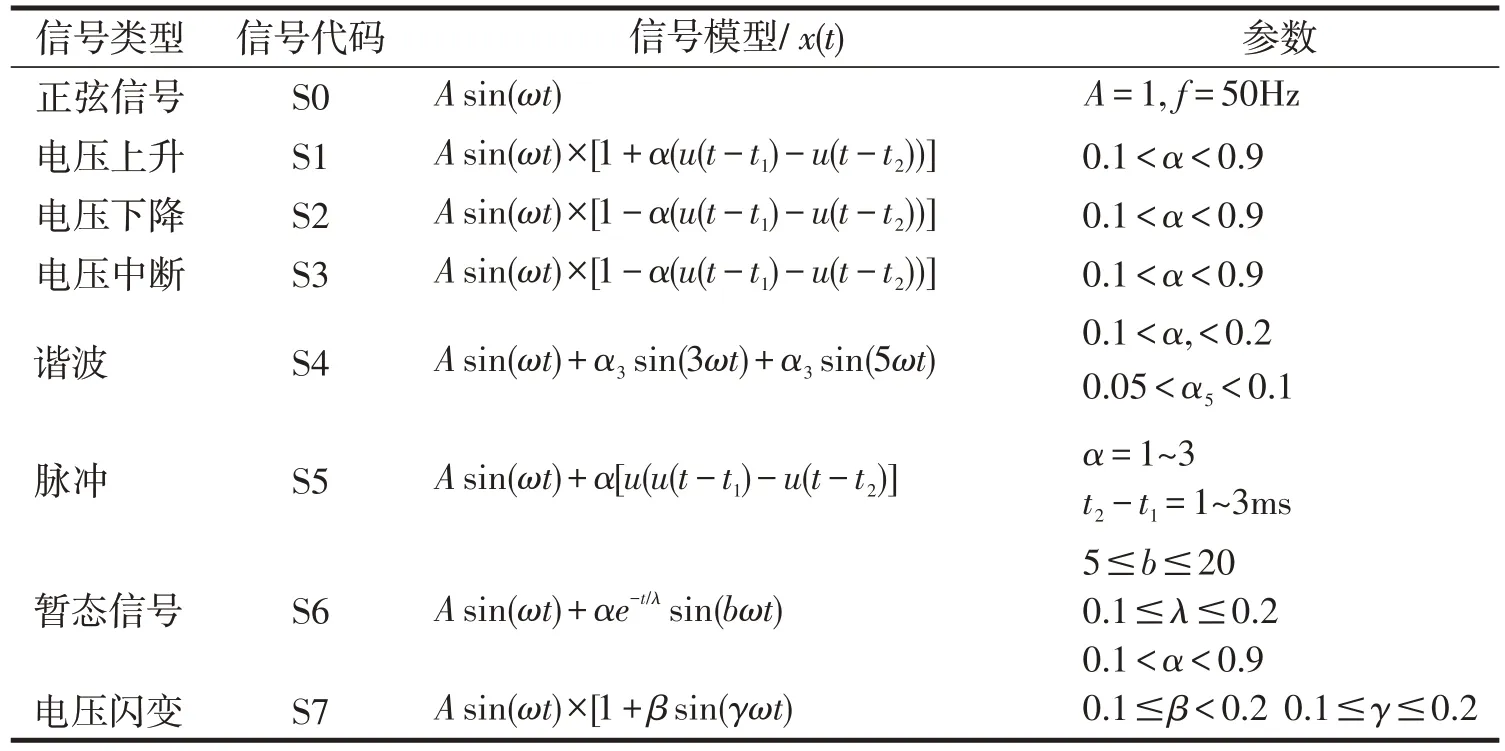
表1 电网扰动信号模型及其参数

3 实验结果分析

3.1 信号模型建立

对电网信号进行数据采集分析，采集时间为2s,采样频率为1024，对8个信号进行了编号，分别用S0～S7来代表8中不同信号，具体信号类型见表1。

本文给出两中不同环境下的信号模型，一种是没有噪声干扰情况下的模型曲线，见图3，一种是加入噪声的信号模型曲线，其中加入的是信噪比为25 dB的高斯白噪声，图形见图4。实际电网中，很难避免噪声干扰，含噪的信号更接近实际情况，从而进一步验证算法的鲁棒性。

图3 无噪声扰动信号模型图

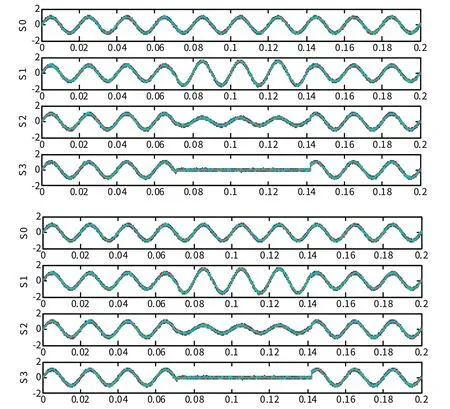
图4 加噪扰动信号模型

3.2 特征提取

采用小波变换对信号进行多分辨分解，采用db4母小波，进行十层分解，根据公式13，公式14，可知WD含有信号的细节信号，最能体现各个信号各自特征，因此，引入帕斯瓦尔定理计算其特征向量能量值，即WD，分别用E0～E10，代表各层数值。在这里对没有噪声情况下的信号进行仿真，WD具体数值见表2。为了更形象直观将各类信号的各层能量进行对比，生成了WD对比图见图5。

由图中可以直观地看出，对信号进行十层分解后，信号的能量主要集中在第七层，有部分信号的能量相对比较接近，如信号S6,S2,两者第七层的能量都保持在63 左右之间，这样要通过提取每层的能量作为特征向量，对部分信号进行识别有很大的难度，并且各个扰动信号的特征向量值均存在上半周。因此，此特征向量不是最佳的特征向量选取值。针对上述问题，本文中选取新的特征向量ΔW进行计算，每种扰动信号的曲线都互相分开，第七层信号能量差都很好的区分开来，每层的具体数值参见表3，其中NEi 代表每层信号的差值ΔW。各层能量值生成的图形见图6。从图中可以看出特征向量ΔW的效果明显好于WD。

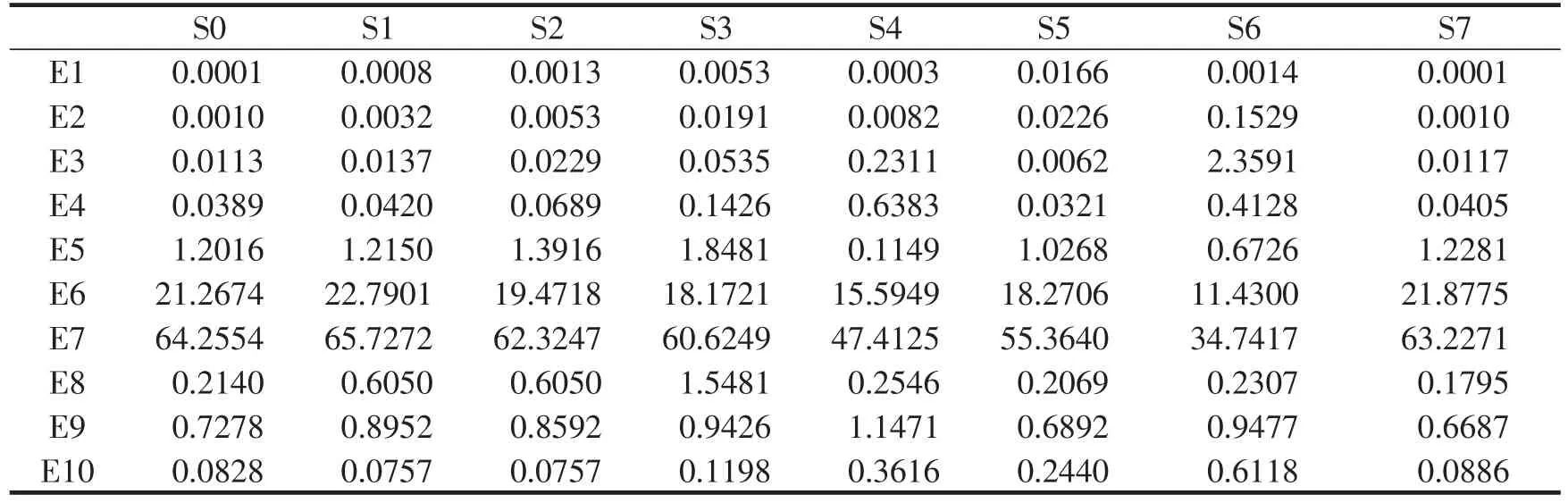
表2 特征向量值WD的各层能量值

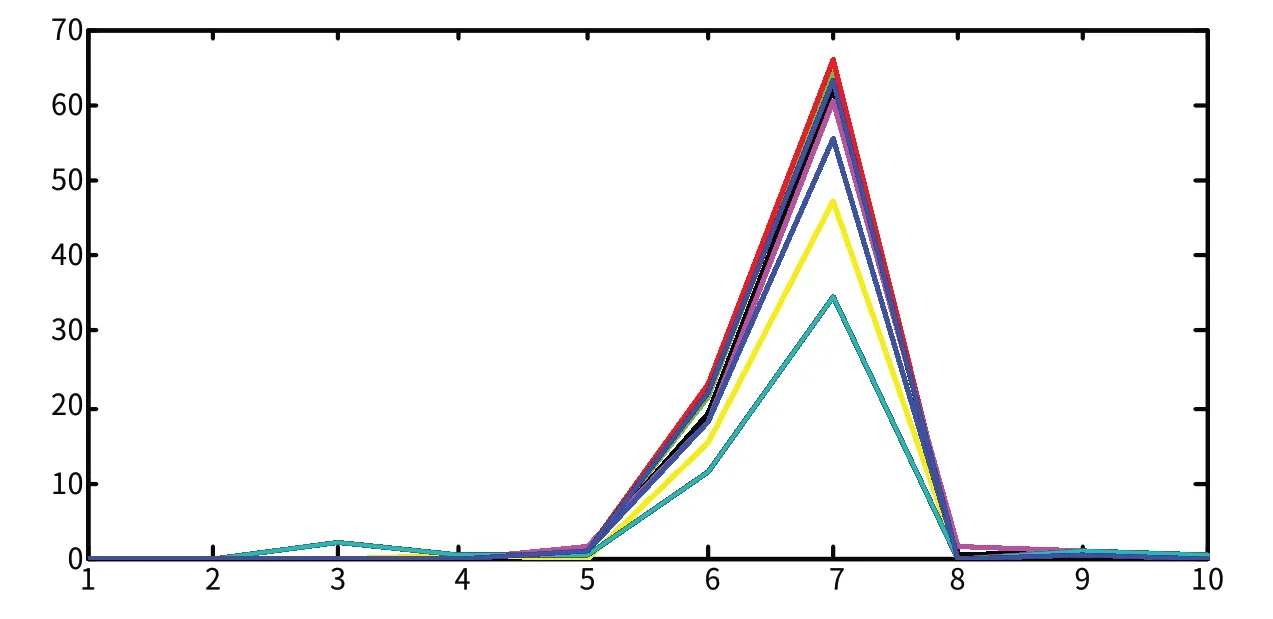
图5 MSD分解后的各层能量WD对比图

表3 特征向量值ΔW 的各层能量值

图6 MSD分解后的各层能量ΔW 对比图

3.3 分类效果对比分析

将特征向量送入分类器进行分类识别，通过样本的分辨率，来验证特征向量的效果。本文选用支持向量机（SVM）作为分类器，图7为无噪声情况下实际分类和测试分类图，通过图形可以看出，实际分类和测试分类样本几乎全部重合，实现较好的分类效果。图8加噪后实际分类和测试分类图，从图中可以看出有噪声情况下，很明显有3个样本出现分类错误，虽然部分噪声出现错误分类，但是整体分类效果不错，绝大多数样本实现了正确分类。

表3给出了采用本文方法和现有两种技术实现的分类效果对比表，文献10 中只给出了无噪声情况下的分类情况，整体分类准备率为97.19%，文献2 给出了信噪比为40 dB，30 dB，20 dB 三种情况下分类正确率，三种情况的整体分辨准备率为97.78%。本文对无噪和含噪的两种方法都进行特征提取，整体分类准确率高于上述两种方法，无噪情况准确率达到100%，含噪情况准备率为99.6875%，见表4[10-11],通过对比，本文的效果较好。

图7 无噪声情况下实际分类和测试分类图

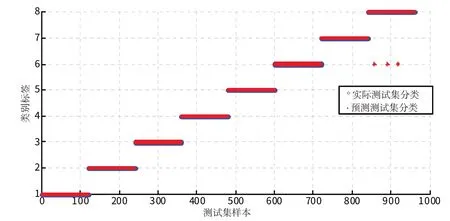
图8 加噪后实际分类和测试分类图

表4 信号整体分类准确率对比表

4 总结

本文针提出一种新的特征向量提取方法，利用小波多分辨率分析和帕萨瓦尔定理，计算能量差值作为特征向量，将其送入SVM分类器，验证分别识别效果。本文建立了八种典型信号模型，分别在无噪和有噪情况下进行试验验证。通过图形和数据分析，此方法的分类识别率高达99%以上，相对现有的现有方法，识别率有了较大的提高，充分证明了该方法可行性、鲁棒性和准确性，为电能质量的提高和电网的治理提供很好的理论依据。