船舶结构振动信号的空间样本扩容

(武汉理工大学 能源与动力工程学院，武汉 430063)

实船振动信号测试过程中，因为船舶结构复杂、运行工况多变或试验成本昂贵等原因导致采集数据不足，容易产生小样本问题。目前的虚拟样本生成技术方法众多[1-3]，虚拟样本扩容方法主要研究针对已有的样本，即当已有样本数量不足时，采取“虚拟样本”生成思想增加样本的数量。在实际的船舶振动信号测试过程中，可能需要得到未知测点的振动信号。针对这一问题，提出“空间样本扩容”概念，并给出利用传递率函数结合有限元方法进行空间样本扩容的方法。

1 空间样本扩容原理

1.1 方法的提出

通过测试手段已经测得某结构的A点的振动信号，但B点的振动信号因为结构复杂或传感器数量不足等原因无法测得，从而造成数据不足。通过测点A的实际已知信号，利用空间样本扩容手段，得到测点B的扩容信号，以增加信号的样本数。见图1。

图1 空间样本扩容示意

1.2 理论基础

1.2.1 传递率函数理论基础

具有n个自由度的振动系统的振动微分方程为

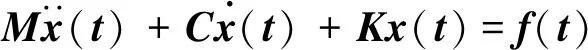
(1)

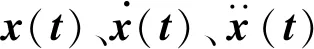
设系统作用激励为

f(t)=Fejωt

(2)

则系统的位移响应为

x=Xejωt

(3)

将式(2)，式(3)带入式(1)可得

(K-Mω2+jωC)X=F

(4)

将式(4)简写为

X(ω)=H(ω)F(ω)

(5)

式中：H(ω)可表示为

H(ω)=(K-ω2M+jωC)-1

(6)

此为振动系统的位移频响函数矩阵，通过推导得到加速度频响函数HA(ω)。

(7)

当外部激励产生的加速度响应由i点传向j点时，根据传递率函数的定义，则加速度传递率函数可以表示为两处加速度响应的比值,即

(8)

式中：Ai(ω)和Aj(ω)分别为在测点i和测点j处的振动加速度响应。根据式(5)，可以进一步推导传递率函数为

(9)

从式(9)可知，在传递率函数中激励只作为激励源而并没有参与运算，因此，结合传递率函数和有限元法进行空间样本扩容时，可以摆脱对于外部激励测量的依赖，相比于直接利用有限元法进行整个振动过程的仿真分析更加简单，适用性更广。

1.2.2 方法实质

在整个结构中，测点O是激励点，测点A的信号已知，测点B的信号未知。见图2。

图2 空间样本扩容示意

根据传递率函数的定义，在结构中点A和点B之间的传递率函数可以表示为

(10)

对模型进行有限元仿真，可得在仿真模型中点A和点B之间的传递率函数可以表示为

(11)

由于在实际情况下的传递率函数和仿真情况下的传递率函数应相等，即

(12)

则进一步可得

(13)

空间样本扩容的思路：在仿真情况下，随机输入激励信号，求取点A和点B之间的传递率函数，然后利用实际的测点A的振动响应信号，计算便可得到未知测点B的实际的振动响应信号，完成空间样本扩容。

1.2.3 扩容的具体步骤

空间样本扩容方法主要步骤。

1)对整个系统进行有限元计算，并根据实际情况确定仿真模型的边界条件和测点的位置。

2)在模型的激励点输入某一随机激励，得到模型上测点A和测点B的响应函数。

4)根据式(13)，利用实际测得的测点A的响应信号，计算得到测点B的振动响应信号。

2 实验验证

2.1 实验设计

实验装置见图3，整个圆盘由一块圆形钢板和2个刚性法兰装配组成。圆形钢板厚为1.6 mm，半径为290 mm。圆盘被2个钢材料法兰刚性夹紧，每个法兰的厚度为32 mm，外环半径为290 mm，内环半径为206 mm。其中薄板的质量为3.25 kg，每个法兰的质量为31.80 kg。薄板两边的法兰盘用10个24M的螺栓紧固在一起，螺栓转矩为100 N·m，整个装配组件悬挂在2个钢制眼上。

图3 圆盘装置

在圆盘的一侧安装5个PCB 352C67型加速度计，通过用力锤敲击圆盘，对圆盘的振动信号进行采集，在实验中使用Bruel & Kjr LAN-XI对加速度信号和力锤信号进行数据采集,数据的采样频率为65 536 Hz。

2.2 数据采集

采用5个PCB 352C67型加速度传感器测量振动信号，传感器灵敏度为0.010 51 V/(ms2);同时，利用Brüel & Kjr LAN-XI数据采集系统对加速度信号和力锤信号进行数据采集，采样时间为2 s，采样频率为65 536 Hz。

为了能更好观察振动加速度信号随频率的变化情况，将时域内的振动加速度信号利用MATLAB软件进行傅里叶变换。主要观察振动加速度信号在0～1 000 Hz内的频域信息，1号加速度传感器测得的振动加速度信号的加速度幅值随频率的变化情况见图4。

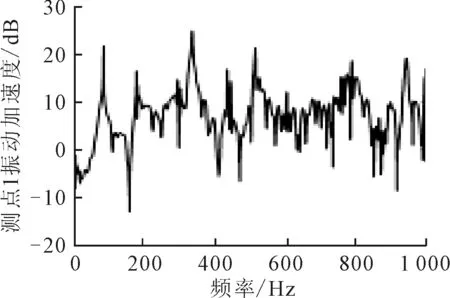
图4 1号传感器的振动信号频谱

2.3 实验模型的有限元仿真及模型验证

利用ANSYS/WORKBENCH对实验装置中的圆盘装置进行仿真。在仿真过程中，材料选取结构钢，具体基本参数：弹性模量为210 GPa，泊松比为0.3，密度ρ=7 872 kg/m3。整个圆盘实验装置的仿真模型见图5。

图5 ANSYS仿真模型

利用ANSYS/WORKBENCH软件中的模态分析模块对整个模型中的圆盘部分进行模态分析，得到仿真圆盘前10阶的固有频率，对比文献[4]提供的通过理论分析所得的固有频率以及模态实验所测的固有频率，结果见表1。

表1 模型的理论、实验、仿真固有频率比较 Hz

由表1可知，仿真得到的固有频率与理论分析得到的固有频率之间的数值差别不大，在实验测试过程中，存在着测量噪声的影响，实验测试得到的固有频率与仿真得到的固有频率之间存在一定的误差，但三者具有较好的一致性；由于圆盘模型是对称结构，在理论、实验及仿真所得的固有频率中，相邻两阶会出现相近或相同的数值的情况。

为进一步证明整个模型的准确性，利用ANSYS/WORKBENCH软件中的瞬态分析模块对整个模型中的圆盘部分进行振动过程分析。将利用Bruel & Kjr LAN-XI数据采集系统采集到的力锤信号输入到仿真模型，得到仿真模型中各个测点的时域振动信号。通过MATLAB软件对时域内的力锤信号和仿真模型上各个测点的振动信号进行傅里叶变换，计算在仿真情况下激励输入点到各个测点的频响函数，将通过实验测得的频响函数与仿真情况下得到的频响函数进行对比。以测点1为例，结果见图6。

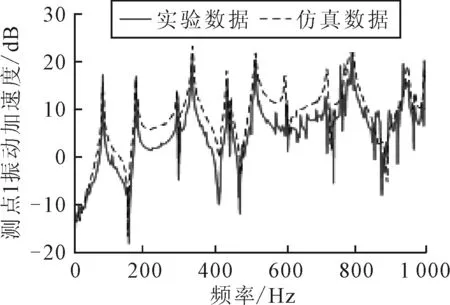
图6 实验与仿真两种情况下点1的频响函数对比

由图6可知，通过仿真得到的频响函数与通过实验测得的频响函数曲线重合度高，在实验与仿真两种情况下，综合固有频率的对比与频响函数的对比结果可知，整个仿真模型与实际的实验装置具有较好的一致性。

2.4 数据扩容结果

在验证仿真模型正确的基础之上进行实际的空间样本扩容。假设测点5的振动信号未知，利用空间样本扩容手段，通过前4个测点的实际振动信号，得到5号测点的虚拟样本。与实际的5号测点的振动响应信号进行对比，以验证文中提出的空间样本扩容方法的可行性。

根据圆盘仿真模型，在实际激励点施加一个幅值为0.5的白噪声激励作为输入，方向沿Z轴，同时采样频率取为2 000 Hz，持续采样时间为2 s。利用ANSYS/WORKBENCH中对整个模型进行仿真分析，得到5个测点在仿真情况下的振动响应信号，计算的传递率函数，见图7。

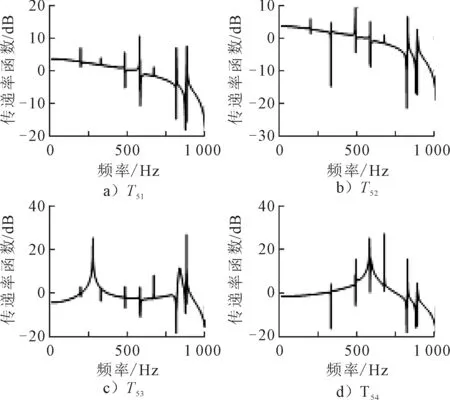
图7 仿真情况下其他测点与测点5之间的传递率函数

在得到传递率函数之后，根据式(13)，便可得到测点5的信号在频率内的变化情况。为验证扩容所得到虚拟样本的正确性，将实验中测得的测点5的信号与通过扩容得到的数据进行对比，观察两者数据曲线的变化情况，结果见图8～11。

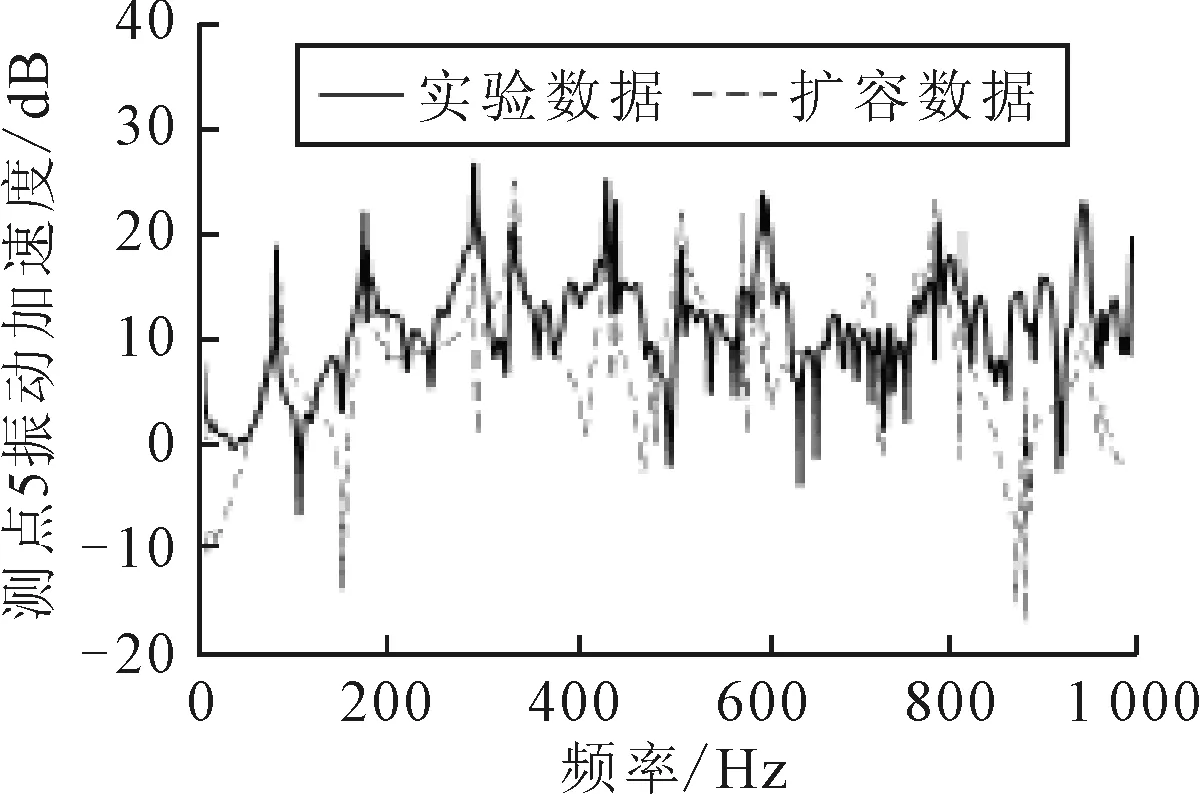
图8 测点5的实验数据与通过测点1扩容得到的数据对比

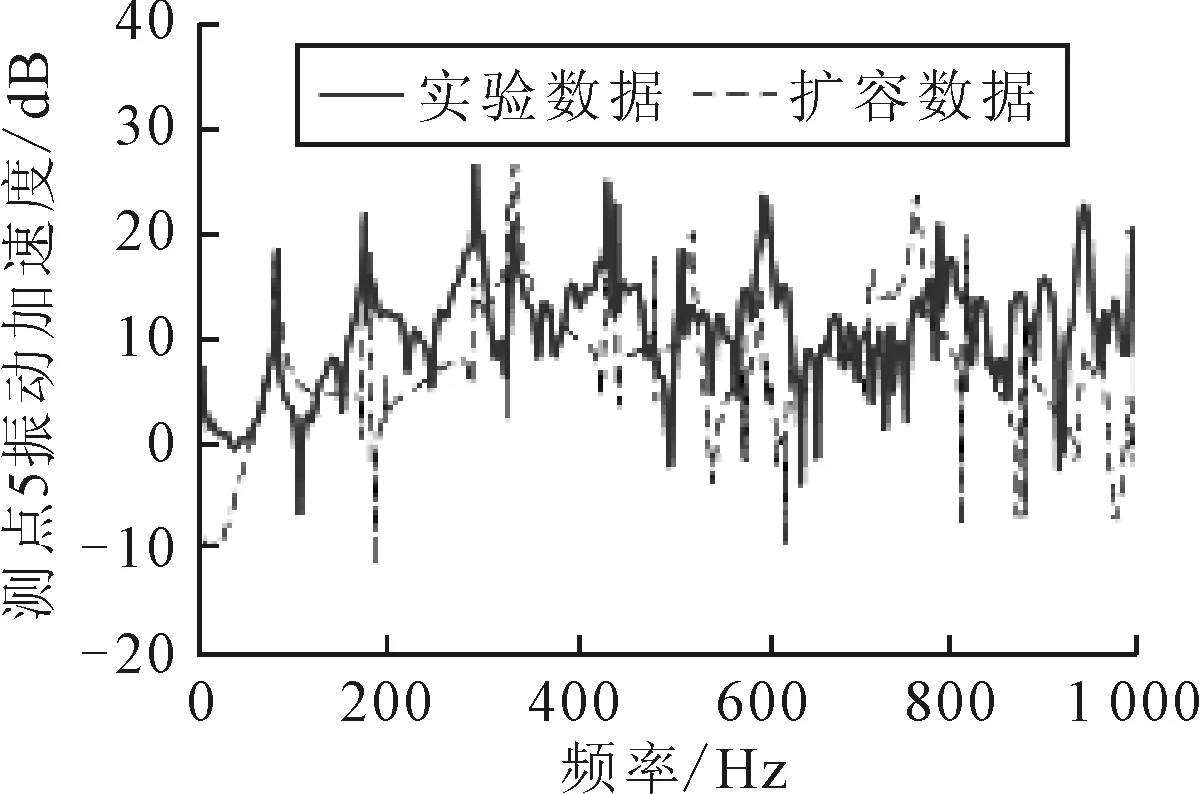
图9 测点5的实验数据与通过测点2扩容得到的数据对比

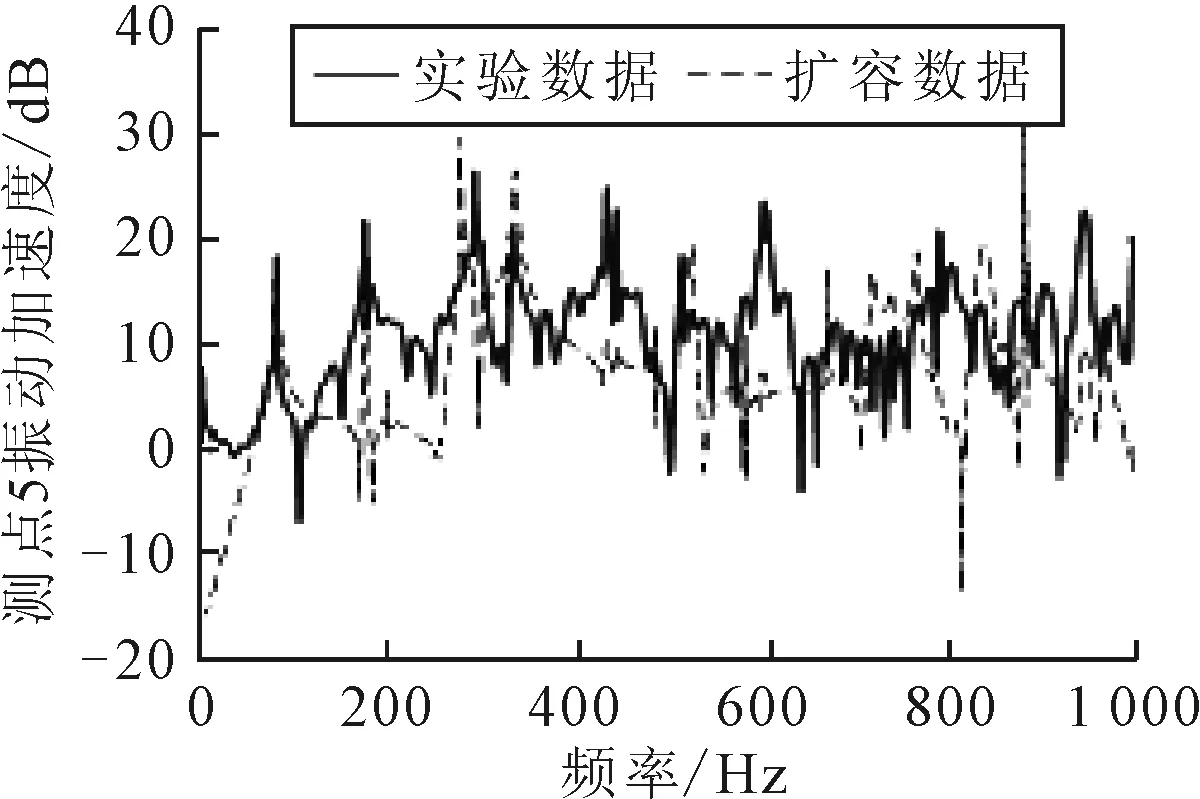
图10 测点5的实验数据与通过测点3扩容得到的数据对比

图11 测点5的实验数据与通过测点4扩容得到的数据对比

由图8～11可知，测点5的实际振动信号与扩容信号两者曲线的幅值变化范围一致，在0～1 000 Hz内二者曲线的变化趋势相近，同时在部分峰值处，两种数据的重合度较高。但由于实际信号存在噪声污染、仿真模型的测点与实际测点可能存在位置上的误差等原因导致实际信号与扩容信号之间存在一定的差异。可以认为通过其他测点得到的测点5的扩容信号具有一定的合理性。

3 结论

1)针对船舶测试中存在的小样本问题，提出结合传递率函数和有限元仿真的空间样本扩容方法，并设计实验加以验证。

2)提出的空间样本扩容可以摆脱对于外界激励测量的依赖，为解决船舶振动信号测量中存在的因结构复杂或传感器数量不足等原因造成的测试样本不足提供一条新的解决思路。

3)就空间样本扩容效果而言，重点在于虚拟样本的准确性，如何尽可能降低虚拟样本与实际样本之间的误差并对误差进行量化，有待进一步研究讨论。