球形耐压壳设计中的稳定性校核

王纬波

(1.中国船舶科学研究中心 船舶振动噪声重点实验室，江苏 无锡 214082；2.常州工程职业技术学院，江苏 常州 213164)

潜水器在水下工作时，主要承受静水压力，大深度载人潜水器的耐压壳常采用球壳结构，稳定性的验算是壳体设计的关键。工程中实际的壳体结构存在各种各样的初始缺陷，对轴压圆柱壳的计算表明，缺陷幅度达到壳厚的1/5，则屈曲临界压力下降约50%[1]。球壳作为一种缺陷敏感性结构，其极限载荷常因为微小的几何偏差而大大降低，分析结构的缺陷敏感度对于确定球形耐压壳的稳定性承载力有着重要的意义。

球形耐压壳在几何缺陷下的稳定性问题，主要通过理论计算和数值分析进行求解，在一定的合理假设下进行理论计算，结合有限元的数值分析，可以得到一些半解析的结果[2-4]。在采用有限元法求解含几何缺陷受压球壳的屈曲问题时，需要将假设的几何缺陷引入到有限元模型中，不考虑制造中残余应力的影响，对完善球壳有限元模型部分节点的初始位置进行修正，得到带有初挠度(即初始几何缺陷)的缺陷球壳模型，再对该模型进行屈曲分析，得到临界屈曲载荷，通过与完善球壳临界屈曲载荷的对比，可以得到结构的缺陷敏感度，从而评估缺陷对球壳稳定承载力的影响。

本文运用一致缺陷模态法、N阶特征缺陷模态法，对初始缺陷下球形耐压壳的稳定性进行分析，探讨2种不同模态缺陷法的合理性和可行性；以设计潜深1 500 m和4 500 m的深潜器耐压球壳为对象，结合模态缺陷法，对CCS《规范》中球壳的强度与稳定性的设计方法进行分析。

1 缺陷模态法与球形耐压壳稳定性

1.1 缺陷模态法

制造工艺和装备工况的千差万别导致结构初始几何缺陷的随机性，在数值模型中引入真实的几何缺陷难以实现，壳体稳定性的设计计算需要能够进行数值模拟且可行的几何缺陷处理方法。

在数值模型中引入几何缺陷时需要解决的主要问题是缺陷形状和缺陷幅值的确定。欧标EN1993-1-6(2007)[5]认为，几何缺陷的形状应取最差缺陷，即导致壳体屈曲载荷下降最快的缺陷，在最差缺陷形状未知的情况下，建议采用模态缺陷来分析壳体的屈曲特性，即引入的缺陷形状基于特征屈曲的各阶模态构型，一致缺陷模态法和N阶特征缺陷模态法，都是基于此原则而发展起来的。一致缺陷模态法利用结构的一阶屈曲模态模拟结构的几何缺陷形状[6]，优点是计算量小，但不能确定第一阶模态缺陷对应的临界屈曲载荷即结构的最小临界屈曲载荷。N阶特征缺陷模态法，用前N阶特征屈曲模态模拟N种几何缺陷形状，计算相应的临界屈曲载荷，取其中的最小值来评估结构稳定性[7]，考虑了高阶模态缺陷对壳体结构稳定性的影响。

1.2 工程算例

以文献[8]中的设计潜深1 500 m的载人潜器球形耐压壳为算例，材料为理想弹塑性，遵循von Mises屈服准则，屈服强度σs=785 MPa，计算水深压力为pj=22 MPa。

EN1993-1-6(2007)中对壳体等效几何缺陷幅值的规定基于壳体的结构制造等级ClassABC，相对理想球壳等效缺陷的最大几何偏差值Δw0,eq定义为

Δw0,eq=max{Δw0,eq,1,Δw0,eq,2}=25tUn

(1)

式中:t为壳体厚；Un为几何缺陷幅值推荐参数，取表1中的推荐值，由本例球壳尺寸，得ClassABC的壳体几何缺陷幅值分别为5.25、8.4、13.125 mm。

表1 几何缺陷幅值推荐参数

利用有限元软件Abaqus对算例进行数值模拟，根据模型参数建立有限元模型。采用4节点缩减积分壳单元S4R，网格大小60 mm×60 mm，选择球壳赤道线上的3个点限制模型的6个方向自由度[9]，球壳网格划分及边界条件见图1。

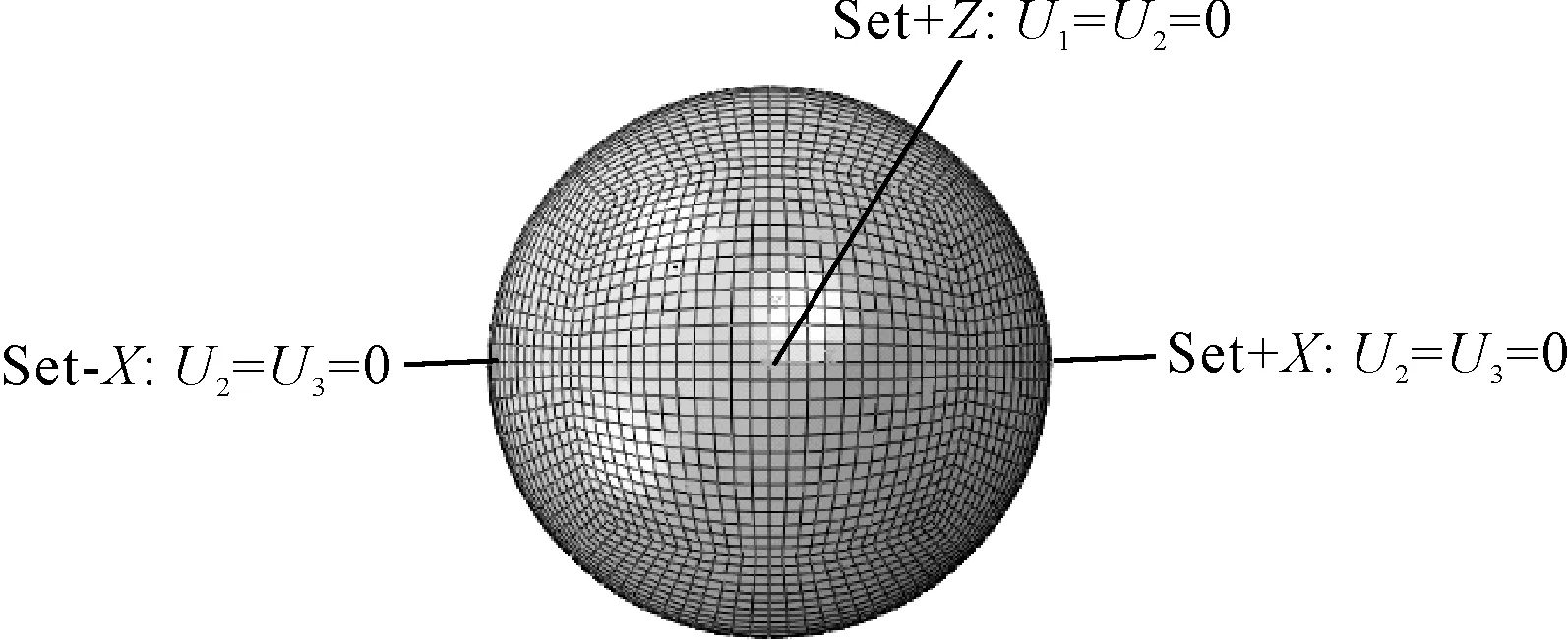
图1 球壳网格划分及边界条件

首先采用一致缺陷模态法进行计算分析，缺陷的引入通过在Abaqus的关键字“keywords”中添加Imperfection语句实现。再运用N阶特征缺陷模态法进行分析计算，取N=20。计算3种缺陷幅值下的临界屈曲载荷，得到3种缺陷幅值对应的最小临界屈曲载荷分别发生在第16、8、16阶模态缺陷下。一致缺陷模态法与N阶特征缺陷模态法得到的屈曲载荷对比见表2。

由表2可见，一致缺陷模态法与N阶特征缺陷模态法得到的屈曲载荷均小于理想球壳非线性分析得到的临界屈曲载荷31.610 8 MPa，一致缺陷模态法得到的3种缺陷对应的临界屈曲载荷大于N阶特征缺陷模态法的计算结果。

一致缺陷模态法与N阶特征缺陷模态法失稳模式对比见图2，一致缺陷模态法的3种缺陷幅值最终的失稳模式相同；N阶特征缺陷模态法，取其最小屈曲临界载荷对应的失稳模式，失稳模式有所不同。

表2 一致缺陷模态法与N阶特征缺陷模态法屈曲载荷对比分析

注：理想球壳临界屈曲载荷非线性计算结果为31.610 8 MPa。

图2 一致缺陷模态法与N阶特征缺陷模态法失稳模式对比

2 CCS《规范》与模态缺陷法球形耐压壳设计计算比较

2.1 耐压球壳强度与屈曲的计算与校核

大深度潜水器的耐压球壳在深海环境下，承受较大的静水压力，为了确保安全性，强度和稳定性要求必须同时满足。

2.1.1 CCS《规范》中球壳强度设计与校核

球壳受压的壳面应力按下式计算[10]。

(2)

式中：pj为设计时的计算压力，取值为

pj=Kρgh

(3)

式(2)所得球壳壳面应力应满足

σ≤0.85σs

(4)

式中:σs为材料强度极限。

2.1.2 CCS《规范》中球壳稳定性的设计与校核

1)1996年版《规范》整球屈曲压力按下式计算[11](1996版《规范》目前已作废，此处取其稳定性设计内容作为参考，与本文方法进行对比验证)。

pcr=CsCzpe

(5)

式中，pe=0.84EC2，C为半径修正系数，可根据比值t/R查文献[11]曲线确定；Cs为材料物理非线性修正系数；Cz为制造效应影响系数，Cs、Cz通过根据σe/σs比值查文献[11]曲线确定，σe=pj/2C。

2)2013版《规范》中潜深大于500 m的潜水器钛合金耐压壳体的极限承载压力计算。

2013版《规范》中“第16章 潜深大于500 m的潜水器的补充规定”，给出了初步设计阶段，承受外压的钛合金耐压球壳的极限承载压力的计算公式为

(6)

式中：Rm为材料抗拉强度；k为制造偏差修正系数，按下式计算。

k=a0+a1x+a2y+a3x2+a4xy+a5y2+

a6x2y+a7xy2+a8y3+a9x2y2+a10xy3+

a11y4++a12x2y3+a13xy4+a14y5

(7)

其中：x=346.74×(Δ/Ri-0.005 5),y=57.7×(t/Ri-0.052 5)；Δ为球壳制造最大允许偏差；Ri为球壳内半径。

2.2 算例

分析对象为设计水深4 500 m的载人潜水器钛合金耐压球壳，安全系数K取1.5，根据式(3)，得计算压力为66.15 MPa，球壳内半径考虑范围为950～1 050 mm，厚度范围为45～55 mm，弹性模量E=1.15×105MPa，泊松比ν=0.3。

文献[12]采用一致模态缺陷法和局部扁壳缺陷法2种方法进行缺陷耐压球壳建模，对0.025≤t/Ri≤0.08，Δ/Ri≤0.01的钛合金耐压球壳进行数值分析。本算例从中选取4 500 m潜水器尺寸范围内，厚度为45、50、55 mm，初始缺陷Δ为0、2、4、8 mm，内径Ri为1 000 mm的3组耐压壳，采用一致缺陷模态法和N阶缺陷模态法，N取前10阶，对上述3组耐压壳极限承载力进行分析，分析结果与文献[12]的2种方法结果进行对比，对比结果见表3。

表3 本算例结果与文献[12]结果对比

由表3可见，本算例方法一与文献[12]方法一均采用一致缺陷模态法，计算结果接近，差值小于1.8%，证实了本算例方法一的正确性；而本算例的方法二，即N阶缺陷模态法，与文献[12]方法二结果略有差异，最大相对误差不超过4.5%，证明N阶缺陷模态法可以作为研究缺陷球壳稳定性的一种方法。

取本算例中4 500 m潜水器最大初始缺陷幅值Δ=8 mm的3组球壳数值分析结果与CCS《规范》理论解进行对比,结果见表4。

由表4可见，本算例3组球壳数值分析得到的中面应力结果与CCS《规范》理论解非常接近，相对误差不超过0.15%；壳厚45 mm的球壳壳面应力不满足强度要求，厚度偏小。

表4 CCS《规范》与本算例壳面应力计算结果对比

注：钛合金屈服极限取σs=800 MPa，0.85σs=680 MPa。

本算例2种方法与1996、2013版CCS《规范》计算得到的极限载荷结果对比见表5。

表5 规范计算与缺陷模态法屈曲载荷计算结果对比

由表5可见，1996版CCS《规范》结果得到的极限载荷值远大于其他3种设计方法，对于设计来说，结果偏危险；本算例一致缺陷模态法与2013版CCS《规范》计算结果很接近，2种方法可以互为佐证；N阶缺陷模态法略小于2013版CCS《规范》计算结果，因为N阶缺陷模态法取的是所有考查范围内高阶模态缺陷对应的极限载荷中，最小的极限载荷值作为结果，所以得到的结果偏保守。所有方法下，厚度55 mm球壳的极限载荷都大于计算压力66.15 MPa，满足稳定性校核；厚度50 mm球壳极限载荷的1996版、2013版CCS《规范》计算结果和一致模态缺陷法计算结果均大于计算压力，但N阶模态缺陷法计算结果小于计算压力，说明如果出现与某一种比一阶屈曲模态更危险的高阶屈曲模态相一致的初始缺陷时，该球壳有失稳的可能。结合上述强度讨论，建议增大设计厚度，事实上，同等球壳内径尺寸下，美国4 500 m潜水器Alvin和我国全国产化4 500 m潜水器的设计厚度分别为49 mm和47.8 mm，都大于45 mm，本算例的强度和稳定性分析符合实际。

3 结论

1)球壳对几何缺陷较为敏感，施加的几何缺陷不同，得到不同的计算结果，球壳的稳定性随缺陷幅值的增大而降低；缺陷的分布形式对球壳的屈曲特性有影响，相等缺陷幅值下，缺陷分布形式不同，得到的临界屈曲载荷不同。

2)模态缺陷法可用于含几何缺陷的球形耐压壳的稳定性分析，一致缺陷模态法的显著优点是工作量小，但第一阶屈曲模态有可能并非结构的最不利几何缺陷构型，求得的承载能力有可能略高估结构的稳定性；N阶特征缺陷模态法考虑了高阶模态对结构稳定性的影响，比一致缺陷模态法的可靠性更高，但计算量太大，在工程应用中的可行性不如一致缺陷模态法。

3)2013版CCS《规范》针对大深度潜水器球形耐压壳稳定性的补充设计公式与数值结果接近，结果可靠性和安全性有较大提高。